---

 

在世界空间下构造相机的世界矩阵

定义相机运动需要的几个参数

• 相机位置x, y, z
• 相机三个轴上的旋转角度，也就是欧拉角，一般把沿x轴旋转的角度叫做Pitch俯仰角，沿着y轴旋转的角度叫Yaw偏航角，以及沿着z轴的旋转角度叫Roll横滚角
• 这样定义的摄像机更适合做自由摄像机
• 而在做相机的目标追踪时，使用起来并不方便

---

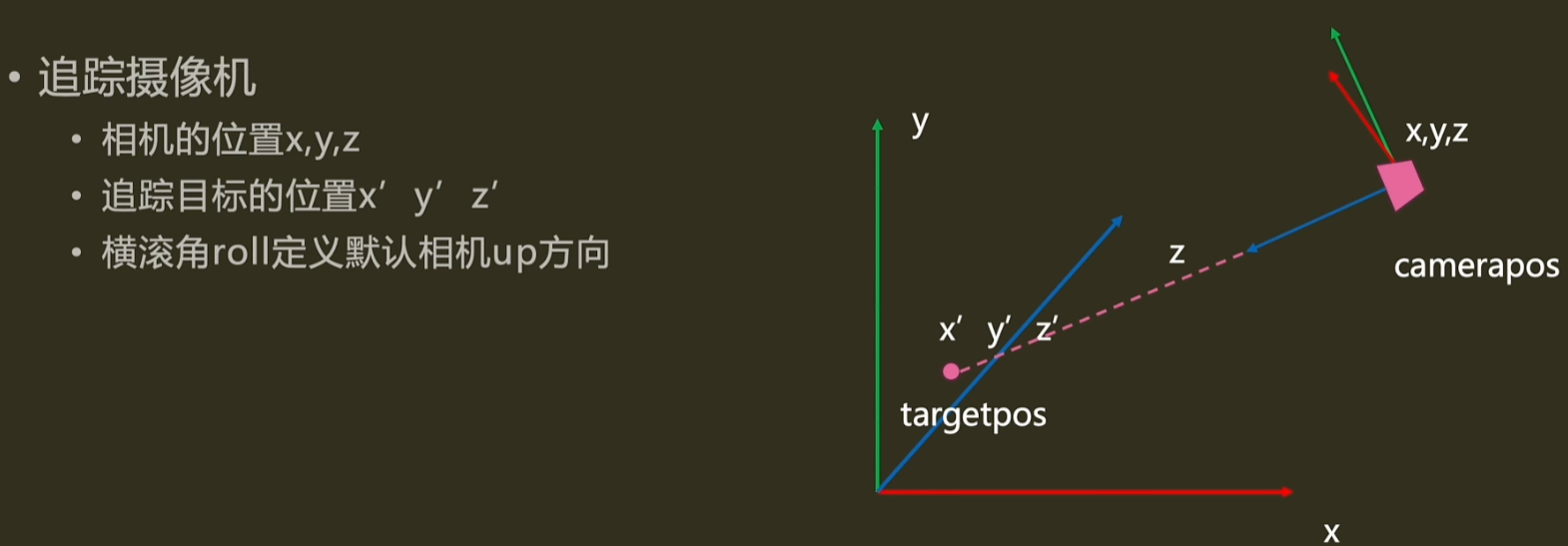
• 对于追踪摄像机，需要的是相机的位置X, Y, Z
• 目标追踪点的位置X’, Y’, Z’
• 由于目标点投影到视口平面后只是一个二维坐标，它只能影响相机沿X轴与Y轴的渲染角度，因此还需要一个变量来控制相机的横滚角度
• 一般情况下相机的横滚角默认为0，也就是相机一般不沿Z轴发生旋转，也就是Y轴朝上
• 不过为了完整性，还是可以通过定义Z旋转轴的Eular角来控制

实现

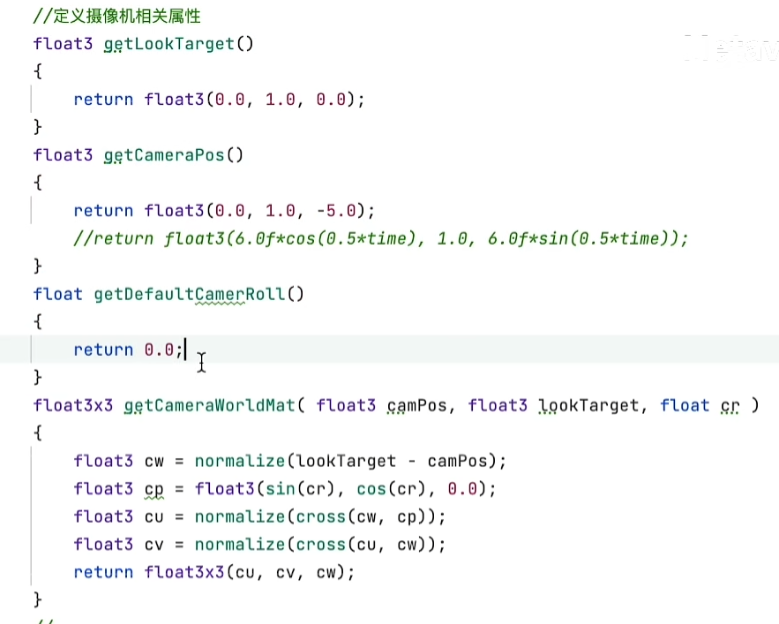
• 将追踪相机的两个矢量参数，一个欧拉角参数设置成函数形式
• 根据这三个参数构建相机的世界矩阵
• 构建相机的世界矩阵的函数中有四个中间变量
  • cw为摄像机的朝向方向，也就是相机矩阵的Z轴正向，是由目标点位置减去相机点位置归一化后得到的
  • cp为世界空间的Y轴正向，这里是由三角函数生成的，为的是方便应用欧拉角参数，默认的欧拉角设置为0，这样实际为float3(0, 1, 0)，也就是世界空间的Y轴正向了
  • 有了两个矢量就可以确定平面了，并可以通过两个矢量的叉乘来求垂直这个平面的向量
  • cu和cv分别代表摄像机矩阵的X轴正向和Y轴正向，也就是屏幕空间下的U方向和V方向。注意叉乘顺序，Unity下是左手坐标系，摊开手掌四指指向的方向代表叉乘的第一个参数，这里也就是世界空间的Y轴正向，握拳四指卷向的方向为第二个参数，也就是Z轴正向，这时大拇指指向的方向就是要求的X轴正向了

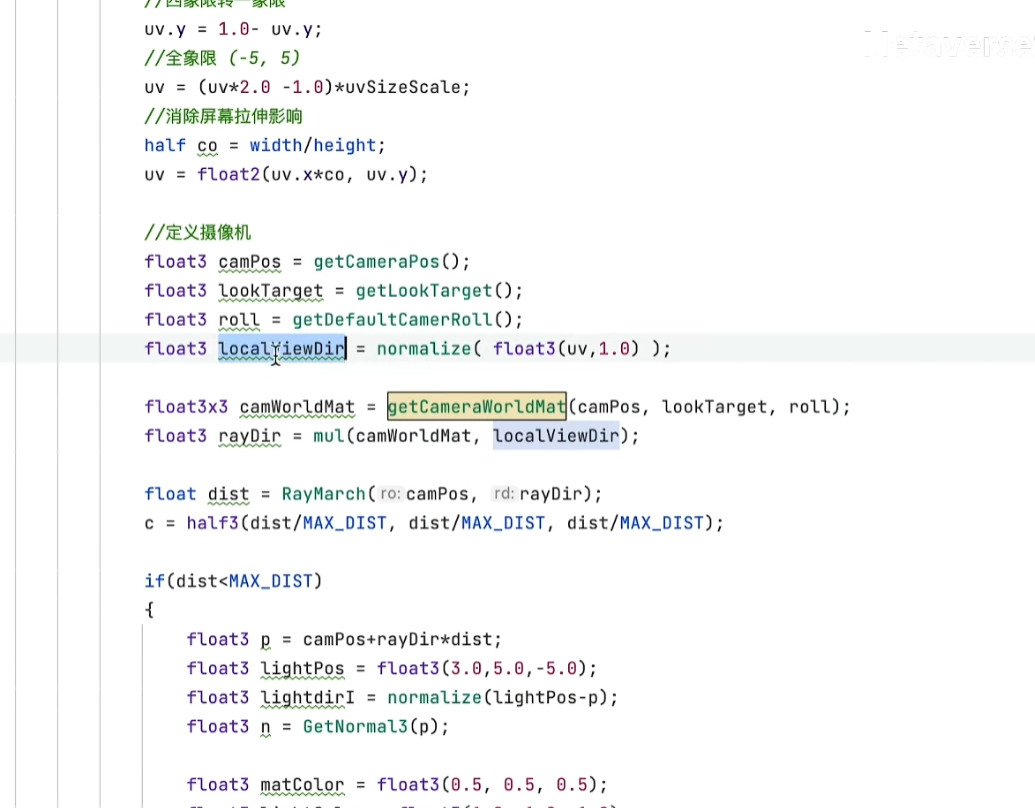
• 有了相机的世界矩阵，需要将矩阵与Ray marching射线步进方向进行组成，这样，3D空间下的成像与摄像机位置、目标点位置以及横滚角联系起来了

• 让摄像机看向(0, 1, 0)点，并做半径为6的圆周运动