本影与半影
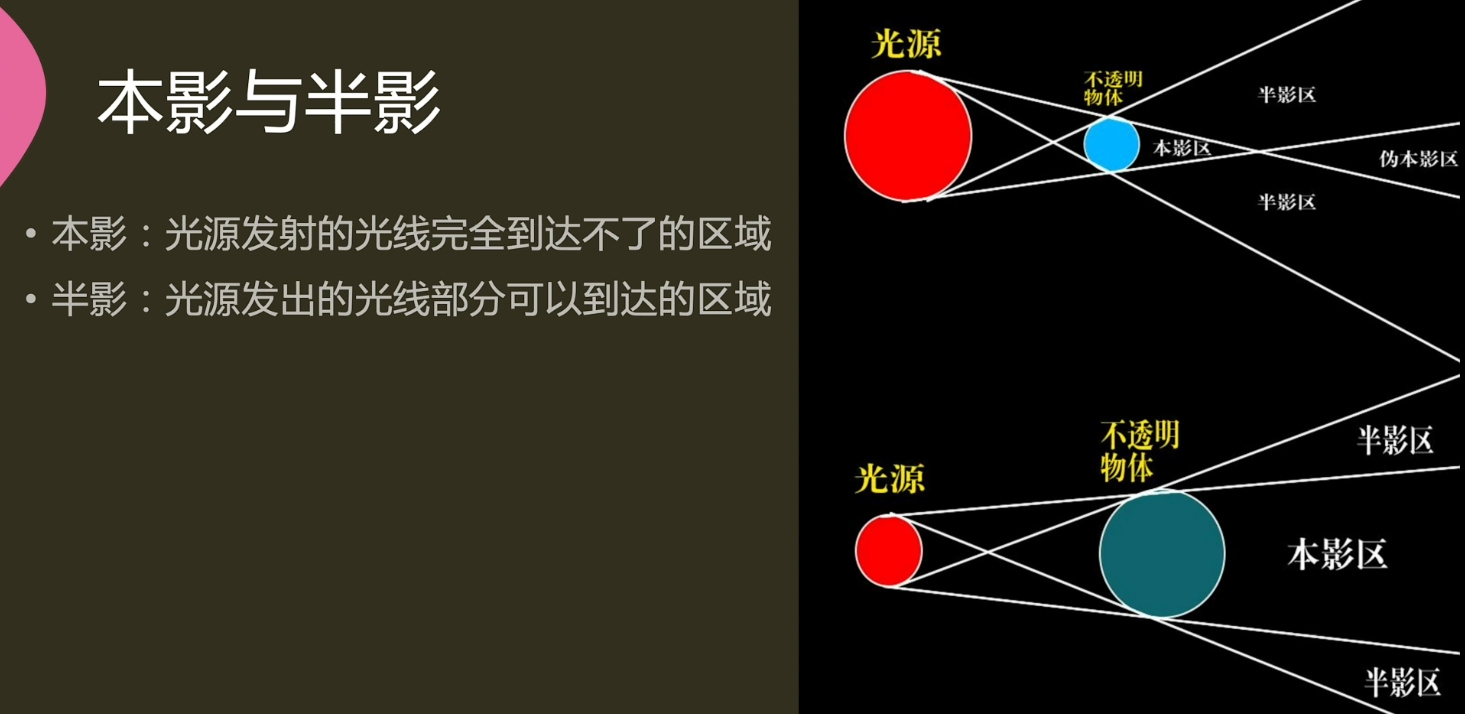
SDF Shadow算法
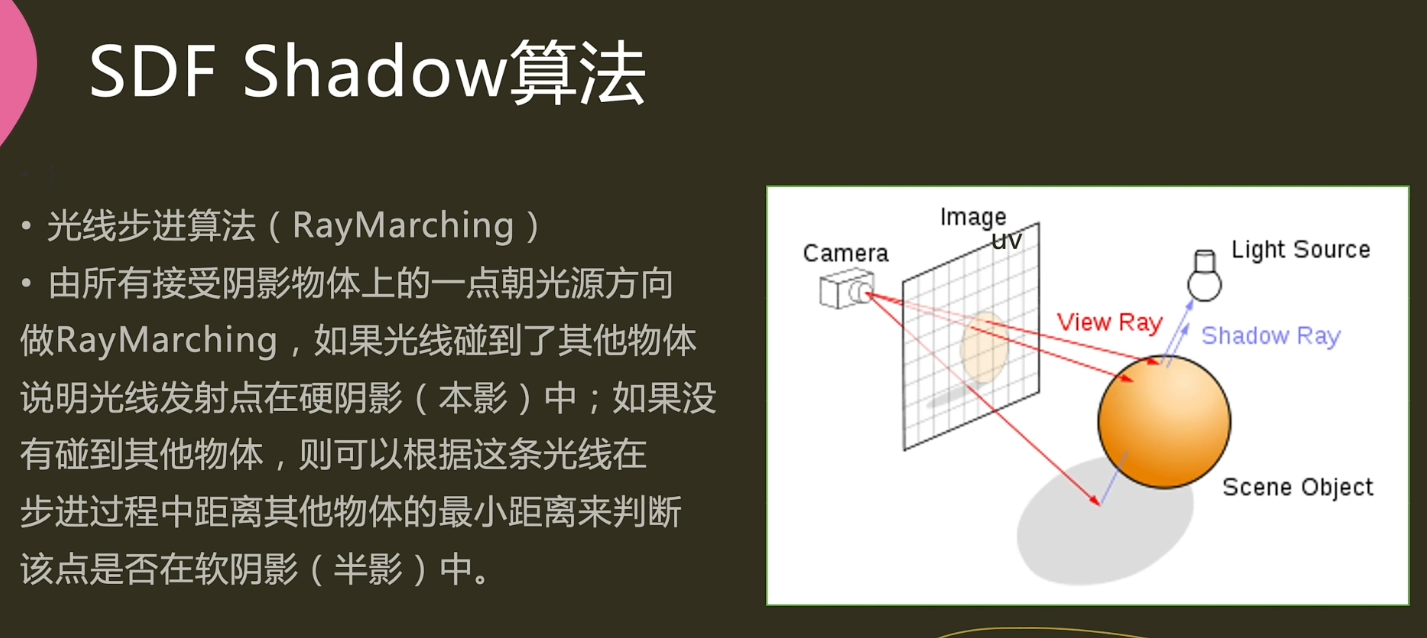
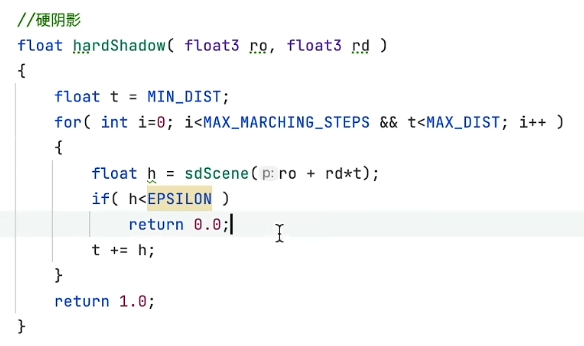
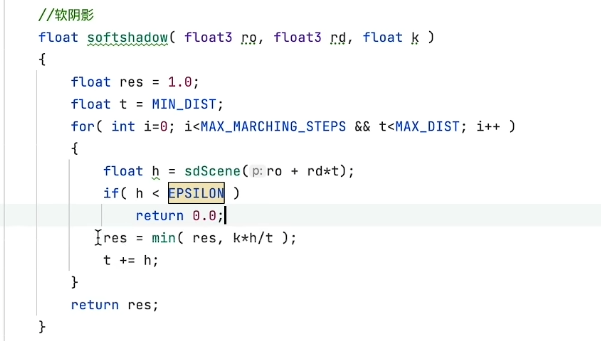
- 当步进距离h小于预定距离EPSILON时,表示光线与物体相交的距离非常小,可以认为发生了碰撞,这时返回0,代表光线发射点的位置在全影中
- 否则,继续进行光线步进
- 当步进距离超过最大距离设定时,表示光线没有与物体发生碰撞,返回1
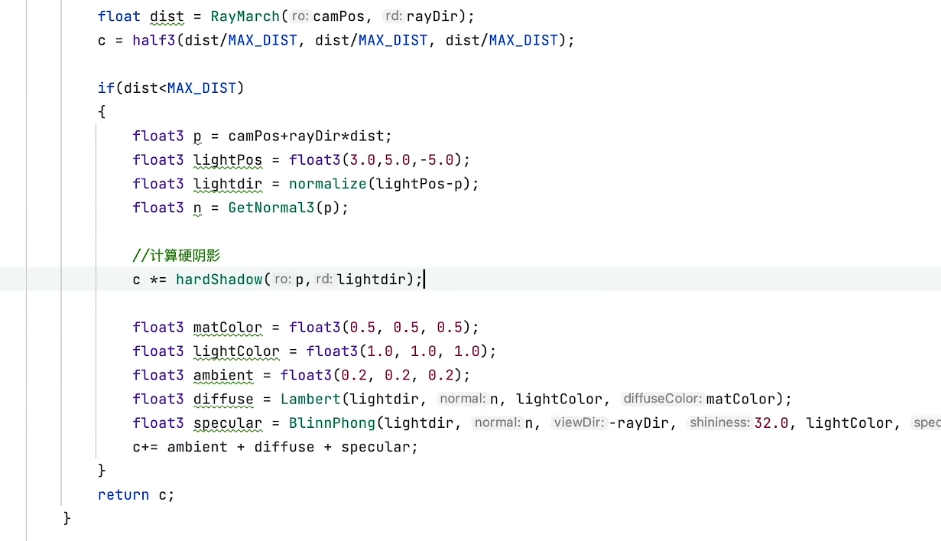
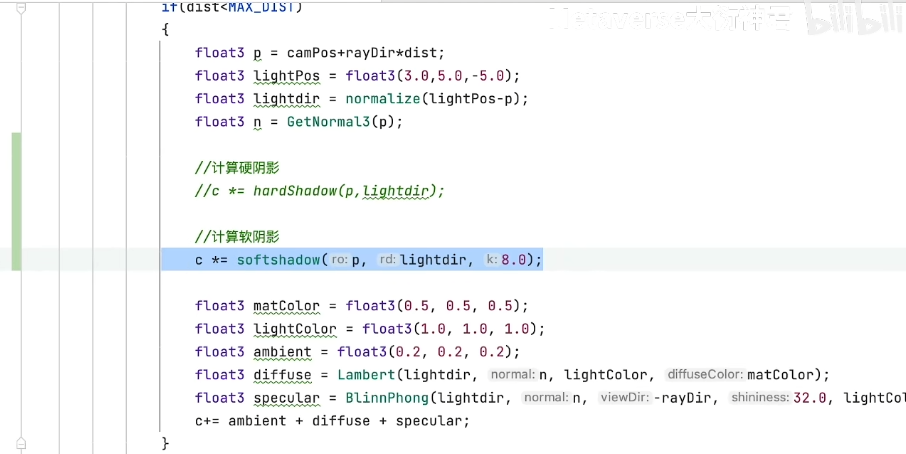
- 调用的地方,传入光源发射点位置p,是计算场景sdf光线步进后,得到的隐式几何体上的点;第二个参数传入光源的方向矢量
- 将计算结果乘以场景深度场
- 由于每个像素计算的结果都是非0即1,其中0代表阴影,1代表非阴影,这样就能得到硬阴影了

- 计算软阴影时,将半影区域返回[0, 1]之间的插值过渡就可以了
- 本影部分逻辑不变
- 通过一个参数k,将原来的非阴影区域根据步进的次数的倒数与k的乘积来表示
- 当k越大时,返回值越接近1,k越小,返回值越接近步进次数的倒数,形成一个过渡区的半影


- 不过这种靠步进次数的插值,中间可能会由于精度产生条带效应,比如步进次数迭代很少的情况下,一些顶点尖角的位置

- 一个改进算法是,通过步进光线到物体表面距离来完成
- 绿点为当前迭代的位置,红点为上次迭代的位置;绿圈与红圈表示当次与上次步进sdf边界相切的球体
- 可以估计最近的几何表面,将位于两个球相交处的点,即两个橙色的点,将这两个点连接起来,就有了橙色线条与光线的交点
- 假设y为绿点到橙点的距离,d为橙色线条的一半,红色与绿色圆圈的半径为r1与r2,可推出y与d的表达式
- 将其引入到软阴影改进算法中
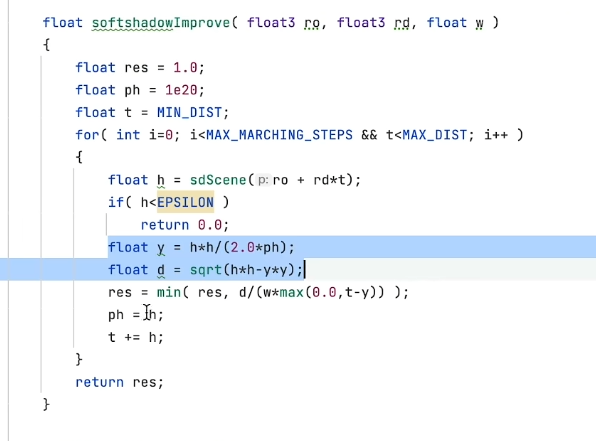
- 这里 d/(w*max(0.0, t-y))就是步进方向与橙点到光源点连线的夹角tan的值
- 而w可以理解为原始软阴影算法中参数k的倒数,这样可以让w的值与软阴影的范围成正比了
小光源与面积光源阴影的差异

- SDF Shadow的内容只适配于光源较小的情况
- 如果光源较大的话可能会出现伪全影的内部半影情况











