- 7.0.1. Advanced Light Transport
- 7.0.2. 有偏/无偏的光线追踪
- 7.0.3. 双向路径追踪(BDPT)
- 7.0.4. Metropolis(人名) 光线传播(MLT)
- 7.0.5. Photon Mapping(光子映射)
- 7.0.6. Vertex Connection and Merging(VCM)
- 7.0.7. Instant Radiosity (IR 实时辐射度)
- 7.0.8. 外观建模
- 7.0.9. 非表面模型
- 7.0.10. Hair Appearance
- 7.0.11. Granular Material
- 7.0.12. Surface Models
- 7.0.13. Cloth
- 7.0.14. Detailed Appearance
- 7.0.15. Procedural Appearance
前言
- 由于内容过多,做笔记太费时间,对于Games101后半段只做简单记录
Lecture 13 Ray Tracing 1
光线追踪
Why Ray Tracing?
- 光栅化最大的问题,就是不能很好地表示全局的效果(软阴影、光线多次反射等)

- 光栅化很快,但质量较低
- 光线追踪真实,但是很慢
- ~10K CPU core hours to render one frame in production
- 光栅化:实时渲染,光线追踪:离线渲染
基本原理
定义光线
- 三个想法(假设):
- 光沿直线传播
- 光线和光线间不会发生碰撞
- 光线肯定是从光源发出,打到场景中,并在场景中不断发生反射、折射等一系列操作后,进入人的眼睛
- 光线追踪利用光线的一个性质,光线的可逆性(reversal-reciprocity),可以理解成,人的眼睛可以发出可以感知的光线,打到物体上,最后打到光源上
- 三个想法(假设):
Ray Casting
- 光线投射:怎样去生成不同的光线
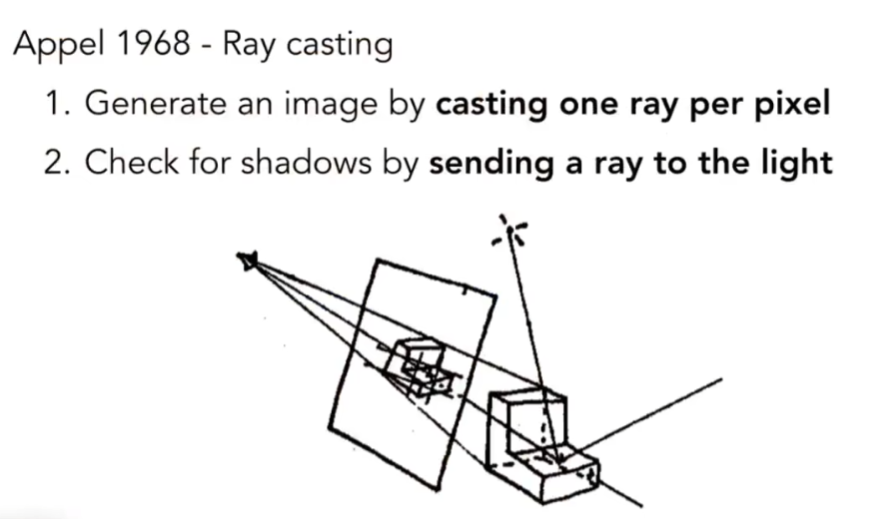
- 从眼睛(摄像机)开始,做光线的投射
- 假设我们向虚拟的世界中看,面前放了一个成像平面,成像平面被划分成不同的像素格子,对每一个格子,可以从摄像机连条直线穿过这个像素,打出一根光线,这根光线一定会打到场景中的某一位置,如果光线和某一物体相交(交点p),表明摄像机沿着这条光线看到哪
- 在把交点(点p)和光源做一个连线,判定这个点是不是对光源也可见,是不是在阴影里,如果不在,则形成一条有效的光路(光源-点p-摄像机)
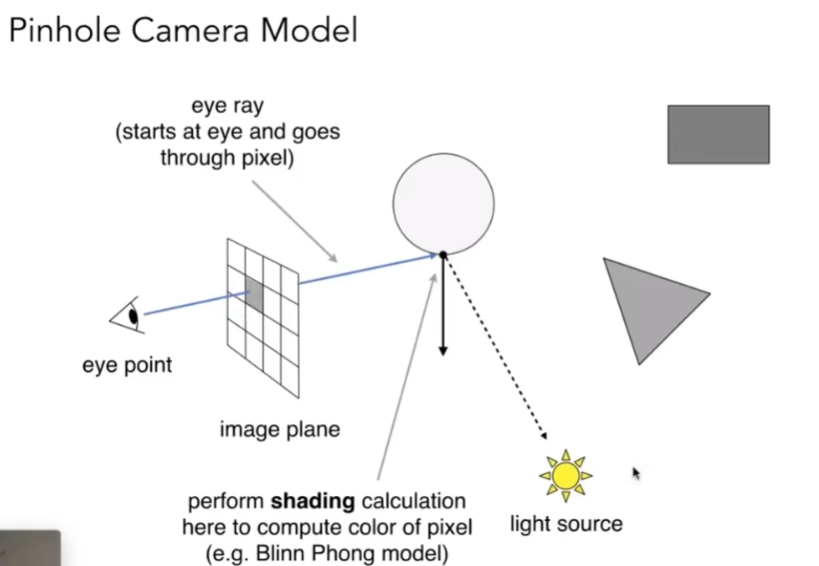
- 每个像素投射出一根光线,从眼睛开始,和场景相交,求对应交点,找到交点后和光源连线,判定是否可见,然后算着色,最后写回像素中
Recursice(Whitted-Style) Ray Tracing

- Whitted风格光线追踪本质是递归
- 考虑光线弹射很多次
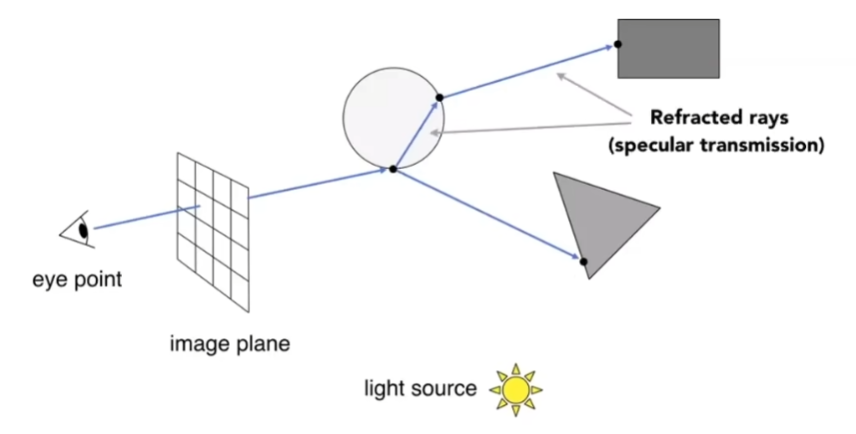
- 在任意一个点可以继续传播这条光线,只需要正确地算出反射方向、折射方向
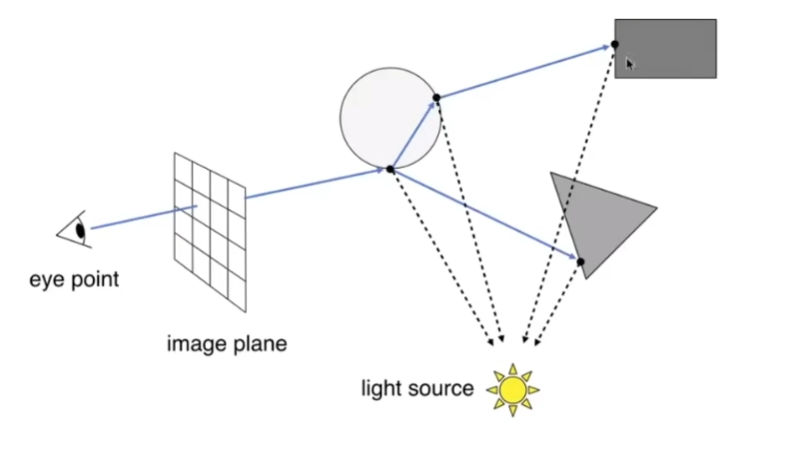
- 着色发生一点点变化,在每一个弹射点都会去计算着色的值
- 如果光源可以照亮任何一个弹射的点,就把这些点算出的着色值都加到像素里面去
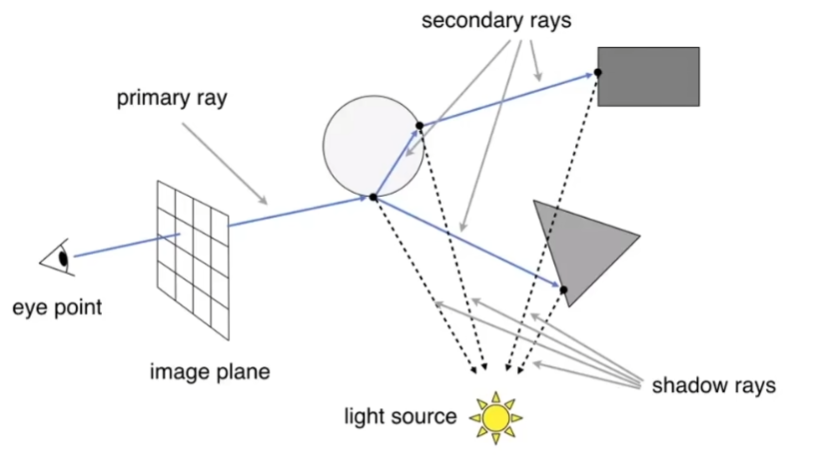
- 将光线进行分类,eye ray(camera ray)归为primary ray;一次以后的弹射称为secondary ray;往光源连接,判断可见性的称为shadow ray
技术细节
如何求交点
- 定义光线,数学上就是一条射线,有一个起点(点光源 o),有一个方向(单位向量 d)
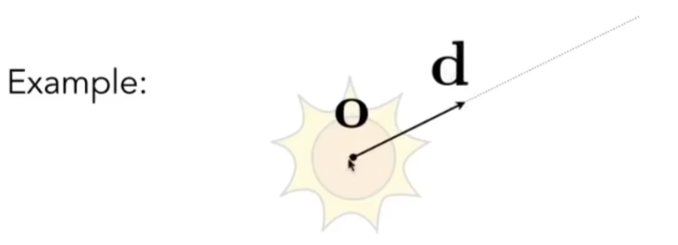
- 光线上任何一个点都可以用公式表达:
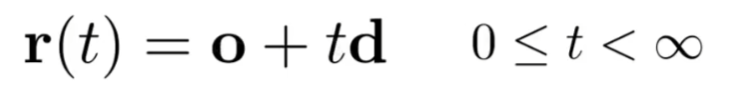
- 定义球,隐函数表示:球上任意一点到圆形的距离都等于半径
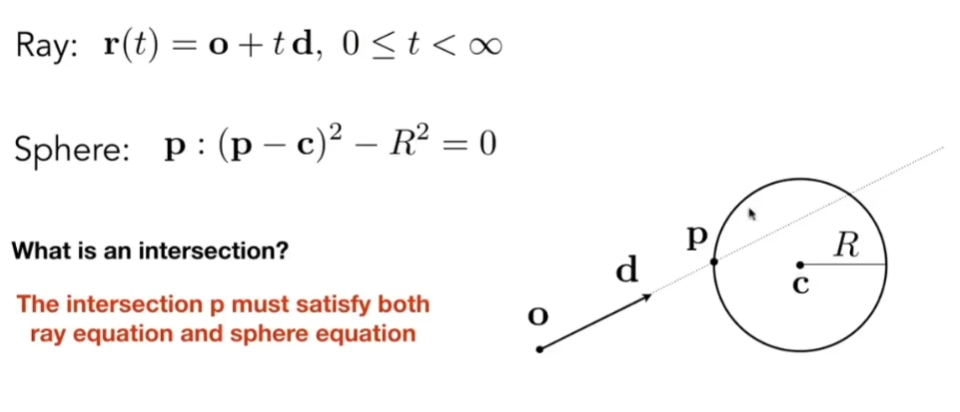
- 要求光线和球的交点,即这个点又在光线上,又在球上,满足表达式:
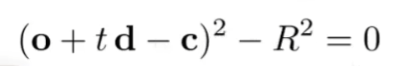
- 即表示沿光线传播多久(t)会落在球上
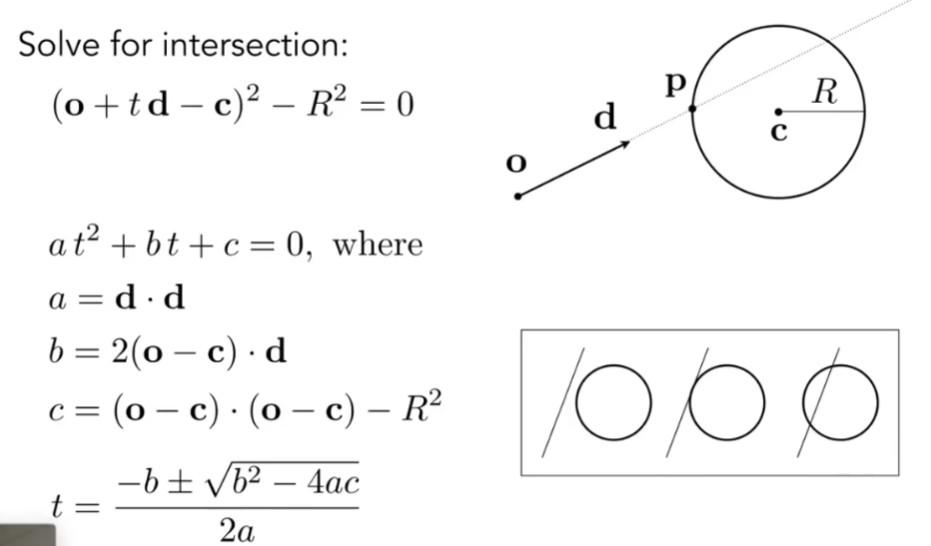
- 将式子展开成二次形式,很容易求得a、b、c的量,同时t得具有物理实际意义,不能为虚数,是正数,根据光线所在射线与球的距离关系,可以解出不同的t
- 推广到光线和一般性的隐式表面的求交

- 解出时间t,交点为o + td
- 对于显式表面求交,即光线和三角形求交
- 在纸上画任何一个封闭的图像,在这个形状内部点一个点,往任意方向做射线,判断光线和物体有多少个交点,会发现,如果点在形状内,得到的交点数一定是奇数;偶数个交点,一定是在物体外。推广到3D一样可行
- 怎样做光线和三角形求交
- 三角形肯定在一个平面内,将问题分解成:光线和平面求交,找到交点后再判断交点是否在三角形内
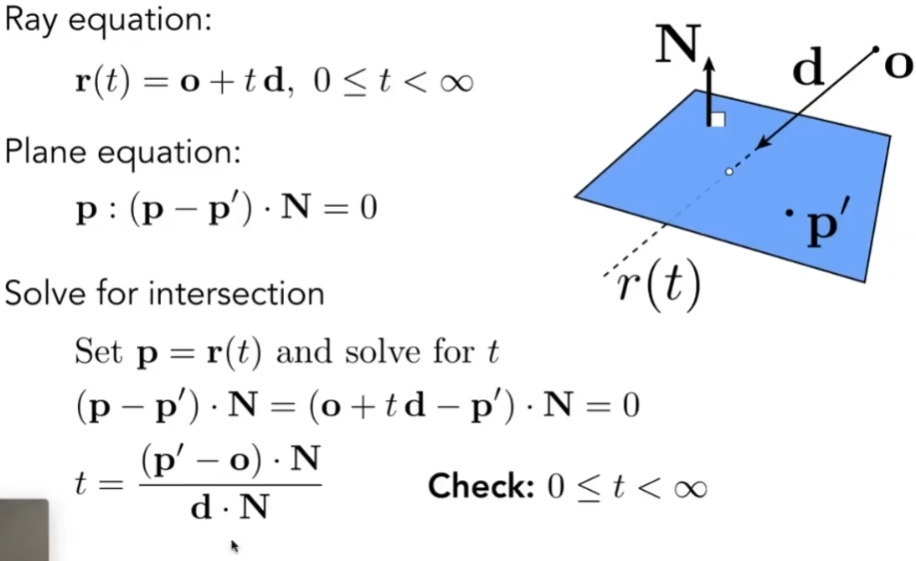
- 定义平面,一个方向和一个点
- 当定义了一个方向(法线 N)后,再定义一个点(p’)就能确定这个平面
- 平面上任何一点p满足:

- 求交点:
- 人们在想,有没有一下解出光线和三角形的交点的方法
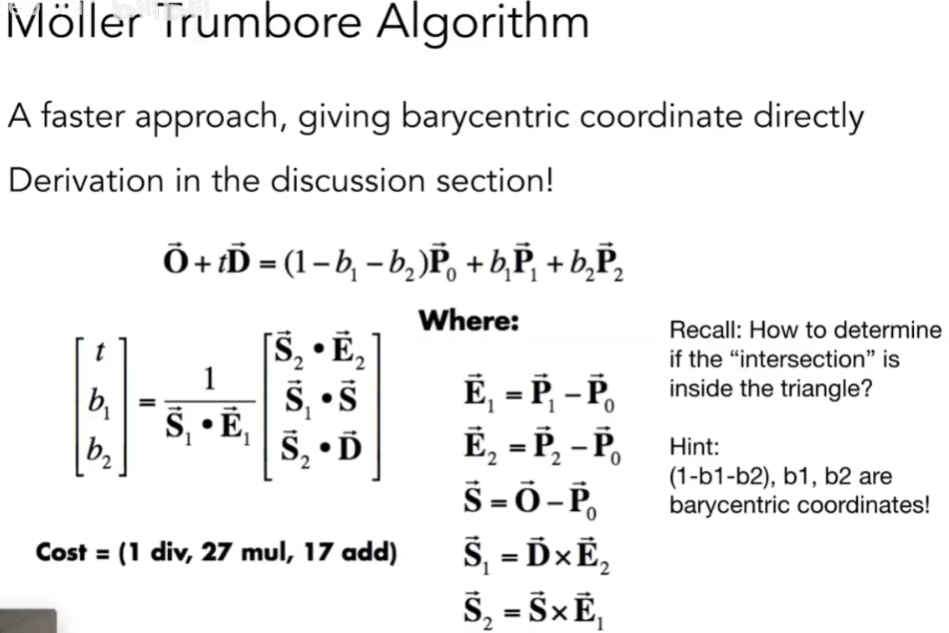
- O + tD 是光线上的点,如果这个点在三角形内,则一定可以写成用重心坐标描述的位置,其中(1-b1-b2)、b1、b2相加为1
- 只需解出t、b1、b2
- 解出后看解是否合理
- 沿着光线方向:t为正
- 点在三角形内,对于重心坐标表示的三角形,1-b1-b2、b1、b2都得是非负的
光线和表面求交点,怎么加速
- 如果用最原始的方法,光线在场景中弹射多次,每次弹射计算一次新的光线和整个场景求交,速度很慢
- 方法一:Bounding Volumes(包围盒)
- 用一个相对简单的形状把物体包围起来,保证物体一定在这个简单形状之内
- 如果光线连包围盒都碰不到,那就更不可能碰到包围盒里的物体
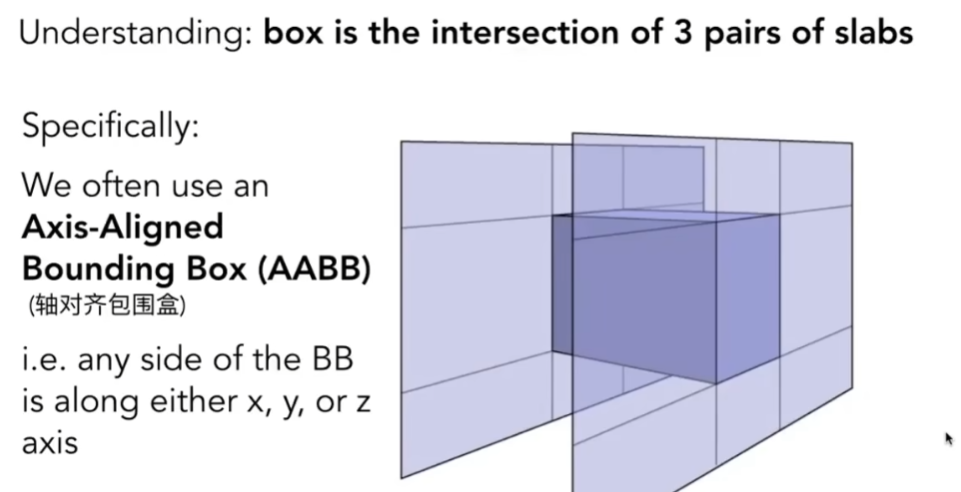
- 将box理解为三个不同的对面形成的交集
- 求交点:
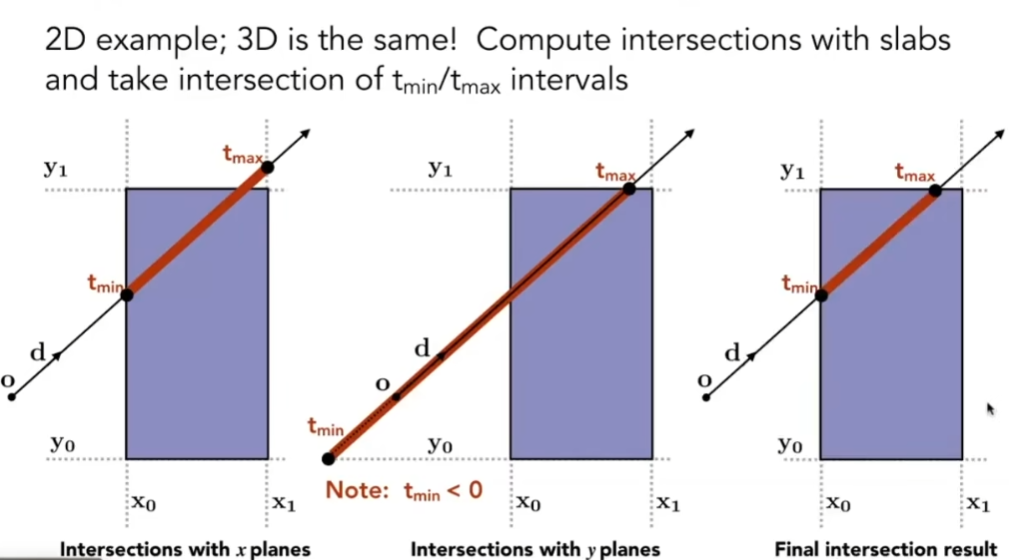
- 对于x0、x1两个面,光线在tmin、tmax时间会和两个面有交点
- 对于y0、y1两个面,光线在tmin、tmax时间会和两个面有交点
- 而光线实际在盒子里的时间,是上面两个线段的交集
- 在三维情况下,有三个不同的对面
- 进入所有的三个对面时认为光线进入包围盒,tenter = max{tmin}
- 只要光线离开任何一个对面,认为光线离开了包围盒,texit = min{tmax}
- 当tenter < texit,表示光线在盒子里了一段时间,有交点;反之则没交点
- 如果texit < 0 ,说明盒子在光线背后,没有交点
- 如果texit >= 0 同时tenter < 0 ,说明光线起点在盒子内,有交点
- 总之,当且仅当tenter < texit && texit >= 0 时,有交点
- 如果用最原始的方法,光线在场景中弹射多次,每次弹射计算一次新的光线和整个场景求交,速度很慢
Lecture 14 Ray Tracing 2
AABB如何帮助加速光线追踪
1.均匀的格子
- 先考虑和包围盒求交,再考虑和物体相交
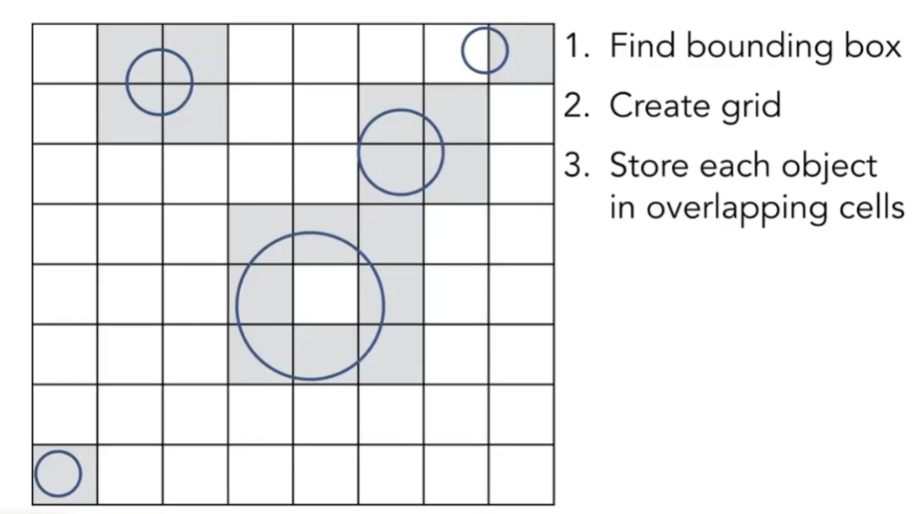
- 在做任何光线追踪前,对场景进行预处理:
- 找到包围盒
- 将包围盒分成一堆格子
- 判定哪些格子和物体表面相交
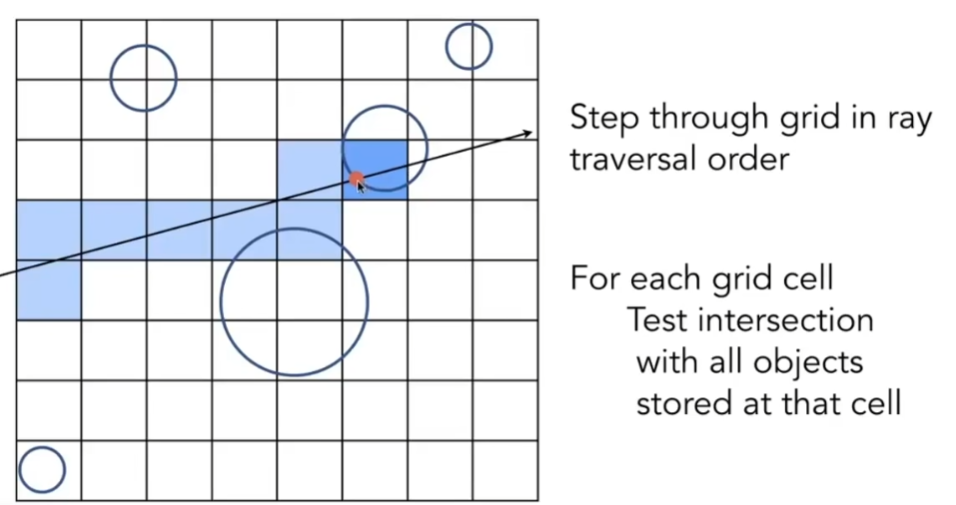
- 做光线追踪
- 假设光线和盒子求交非常快,和实际物体求交非常慢
- 当光线经过的格子内有物体,则该格子内,光线和物体有可能有交点,这时再做光线和物体求交点
- 通过光线的传播方向,判定接下来需要求交的格子是哪几个。如向右上打的光线,只需判断其上方和右方的格子
- 划分的格子不能太密也不能太疏,得有一个平衡
- #cells = C * #objs
- C ≈ 27 in 3D
2.空间划分
- 均匀的格子有许多不足之处,如在稀疏的地方不需要那么多格子
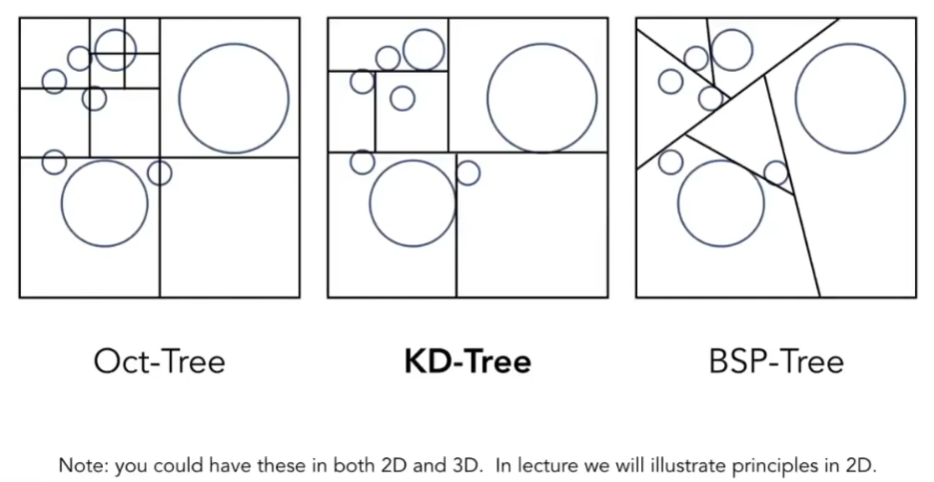
- 八叉树
- 一个节点有八个子节点
- 通过一定规则来规定停止切分的标准
- 人们不喜欢用八叉树:在二维下是四叉树,三维下是八叉树,若维度再高点,就变成2的幂次树,显然并不好
- KD-Tree
- 能让空间得到划分,并且和维度没关系
- 每一次找到一个格子,总是将它沿着某一个轴进行展开,只切一刀
- 每个轴交替切分,基本保证均匀地划分
- BSP-Tree
- 每次将空间进行二分,但不是横平竖直的,类似KD树,但计算上跟复杂
- 维度高时,计算会越来越复杂
KD-Tree
- 同样是做光线追踪前的预处理
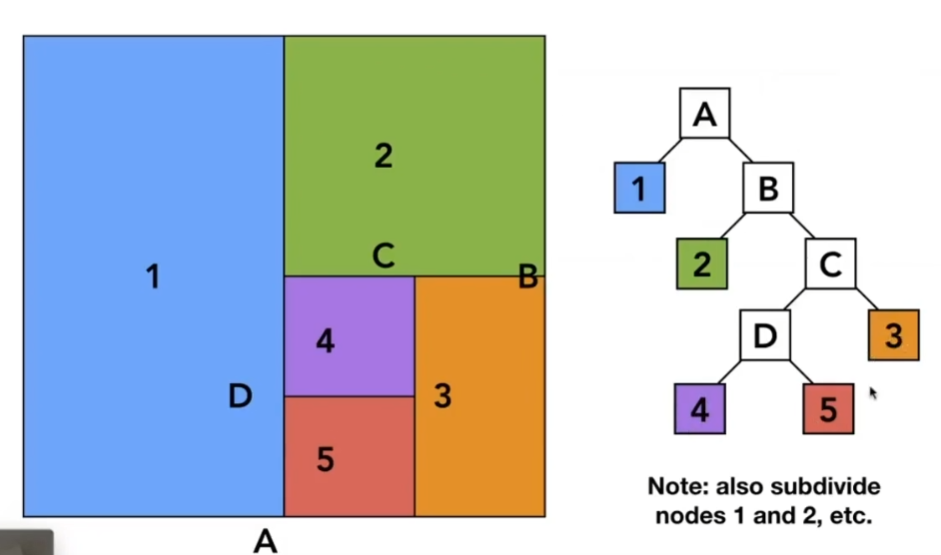

- 如果设计一种数据结构来存储KD-Tree
- 对于任何一个节点
- 当前沿着哪个轴划分
- 划分在哪
- 对于中间节点来说一定有两个子节点
- 实际的物体(三角形)只存在叶子节点上
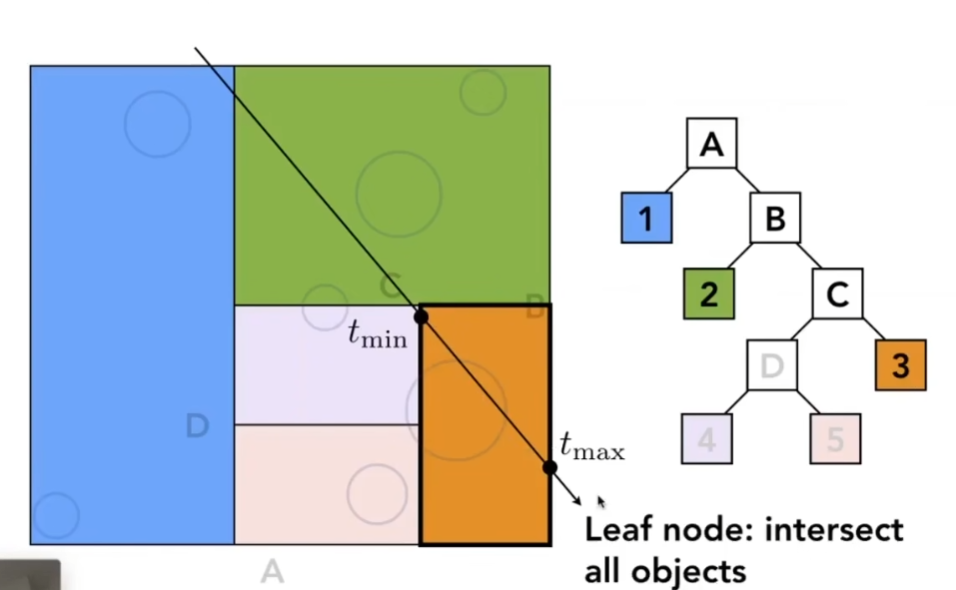
- 实际做法:
- 如果光线和某一格子没有交点,什么都不用做
- 如果光线和某一格子有交点,就能知道,光线和它的两个子节点可能都有交点,所以都看一下,直到光线打到叶子结点,如果还没有交点,什么都不用动,如果和叶子节点包围盒有交点,则光线和包围盒里所以物体进行求交
- 但是,如何判定场景中的物体(三角形)和包围盒相交,是个复杂的问题;一个物体可能出现在多个包围盒里,并不直观
- 因此,人们渐渐地不使用KD-Tree了
- 于是有了另外一种办法,同样可以做划分,不是从空间做起,而且从物体做起,形成的加速结构,就叫做BVH
Object Partitions & Bounding Volume Hierarchy (BVH)
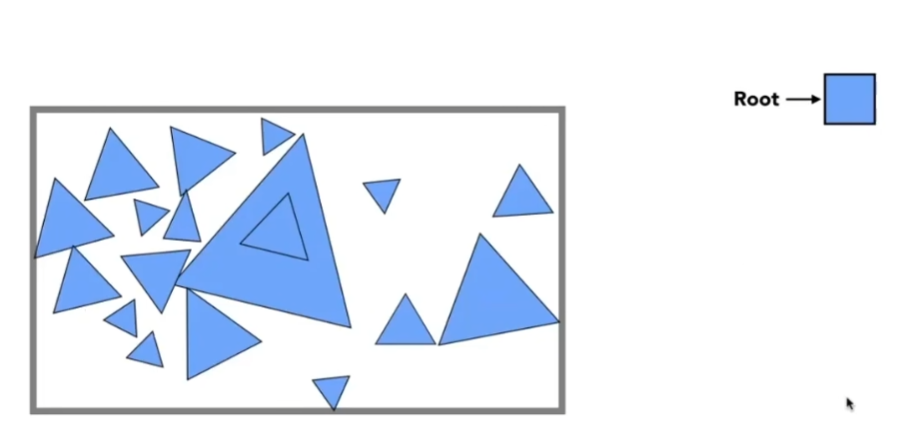
- 一开始找一个盒子把全部物体包起来
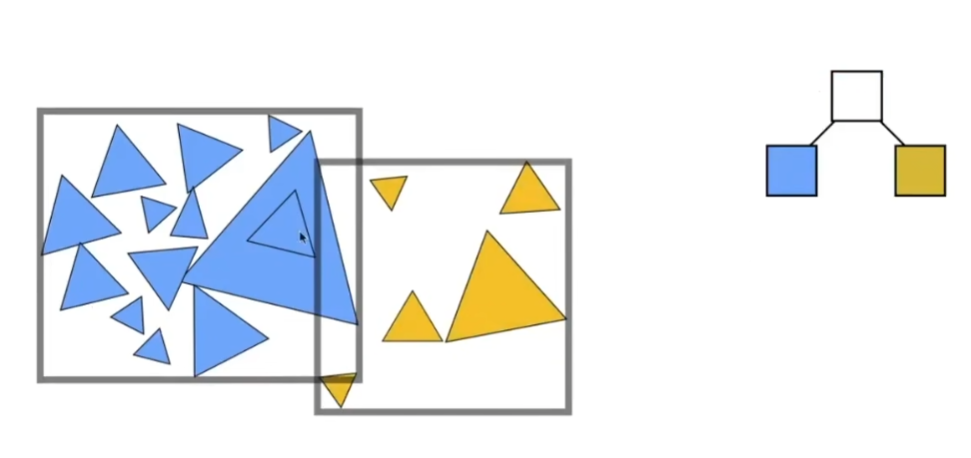
- 将所有三角形分成两部分,把这两部分的三角形重新求它们的包围盒
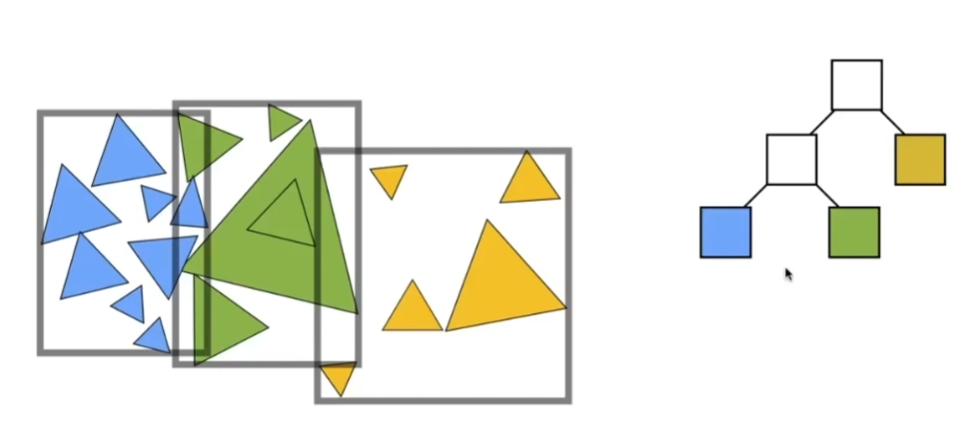
- 可以明确的是,一种物体只可能出现在一个格子里,省去了三角形和盒子求交点,避免了KD-Tree的问题
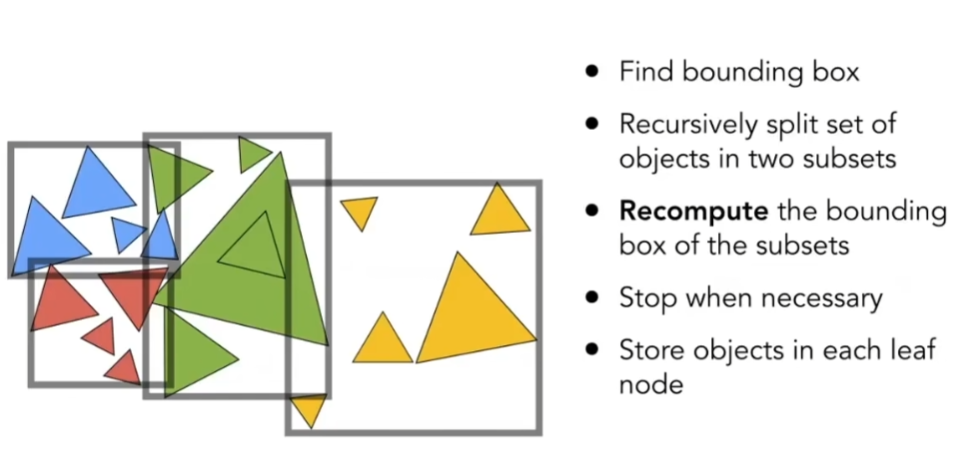
- 实际做法:
- 找到一个包围盒
- 递归地把任何一个包围盒拆成两个部分
- 把这两部分重新计算包围盒
- 正常情况下,当叶子节点有足够少的三角形时,停止划分
- 如何划分节点有不同的做法:
- 沿着最长的轴:保证划分的空间较均匀
- 取中间的物体:两部分的三角形数量差不多,划分成的树较为平衡(深度差不多)
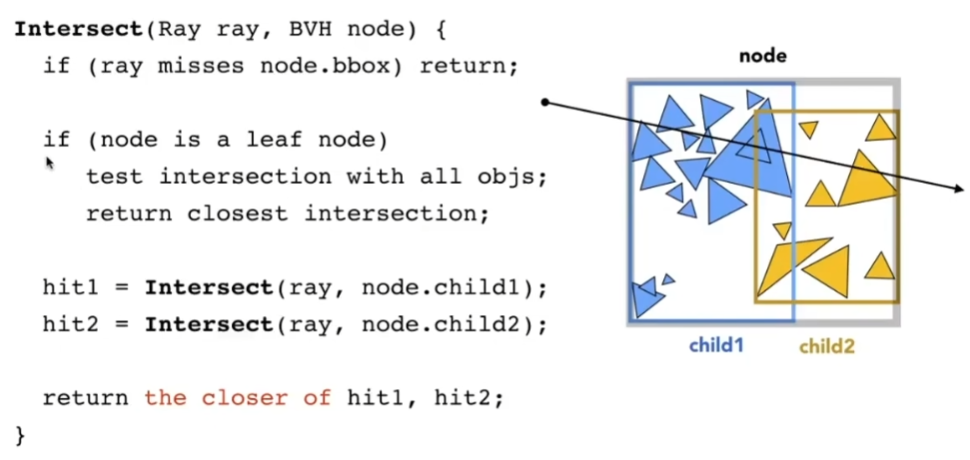
- 如果光线和整个BVH节点都不想交,什么也不发生
- 如果相交,是叶子结点,则光线和节点内所有物体求交,返回最近的那个
- 如果相交,不是叶子结点,则光线可能和两个节点都有交点,分别求出它们两个的交点,再求最近的一个(递归)
Basic radiometry(辐射度量学)
- 学习辐射度量学的动机
- Blinn-Phong模型中提到,Light intensity I = 10,这个10是什么呢,肯定得有个物理意义
- 辐射度量学告诉我们如何去定义光照,定义了一系列方法和单位,可以给光各种各样不同的(空间中的)属性
- 认为光还是沿直线传播,不会波动
- New terms:Radiant flux, intensity, intensity, irradiance, radiance
- 所有这些量都有明确的物理概念
Radiant Energy and Flux(Power)
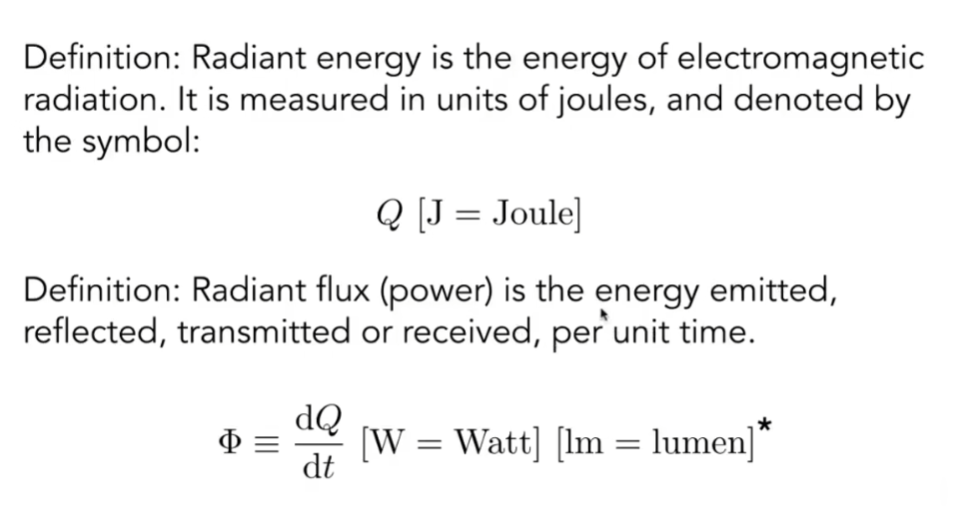
- Radiant Energy,是一种能量,用焦耳单位表示
- Radiant Flux,人们通常叫它Power,单位时间内产生的能量,类似功率,单位为瓦特
- 可以理解为光的亮度
- 另一种理解:有一个感光的平面,单位时间通过它的光子的数量,就是它的flux
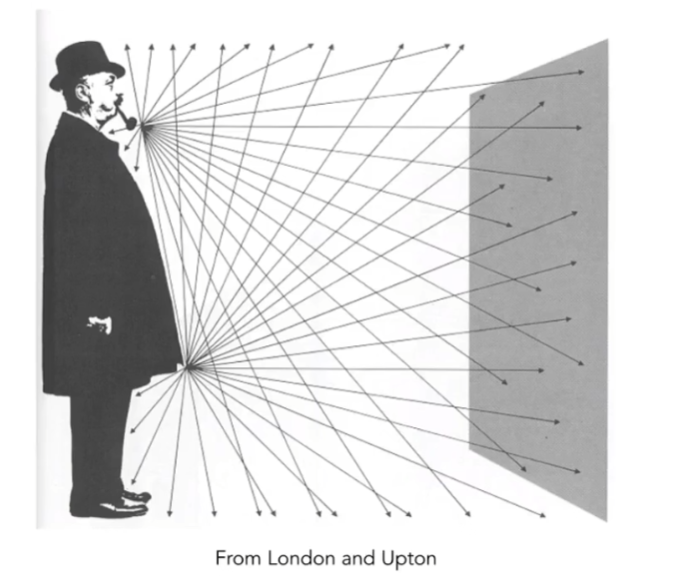
- 一个灯泡看上去更亮,说明单位时间内辐射出更多的光子
Radiant Intensity & Irradiance & Radiance
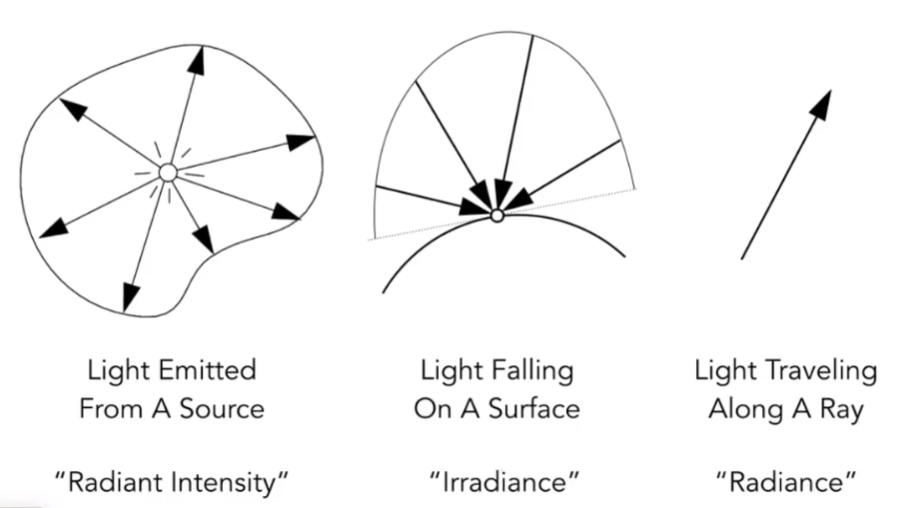
- Radiant Intensity:
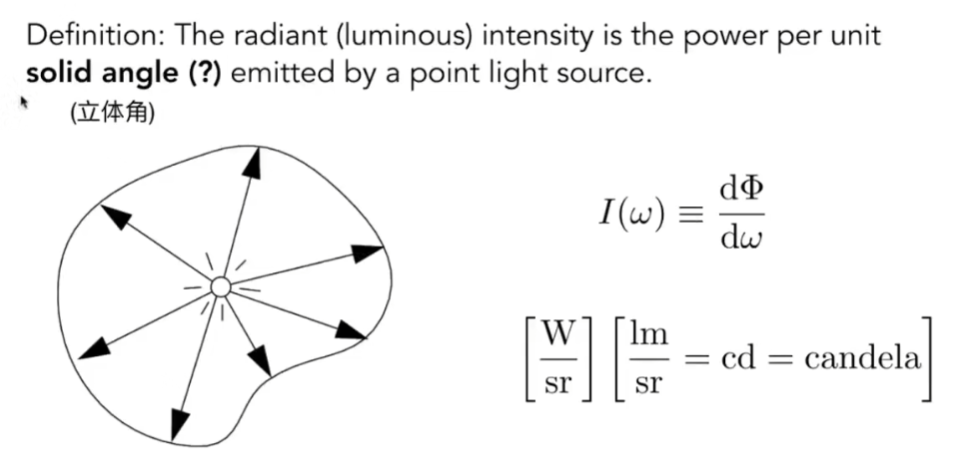
定义:单位立体角上的Power
立体角:
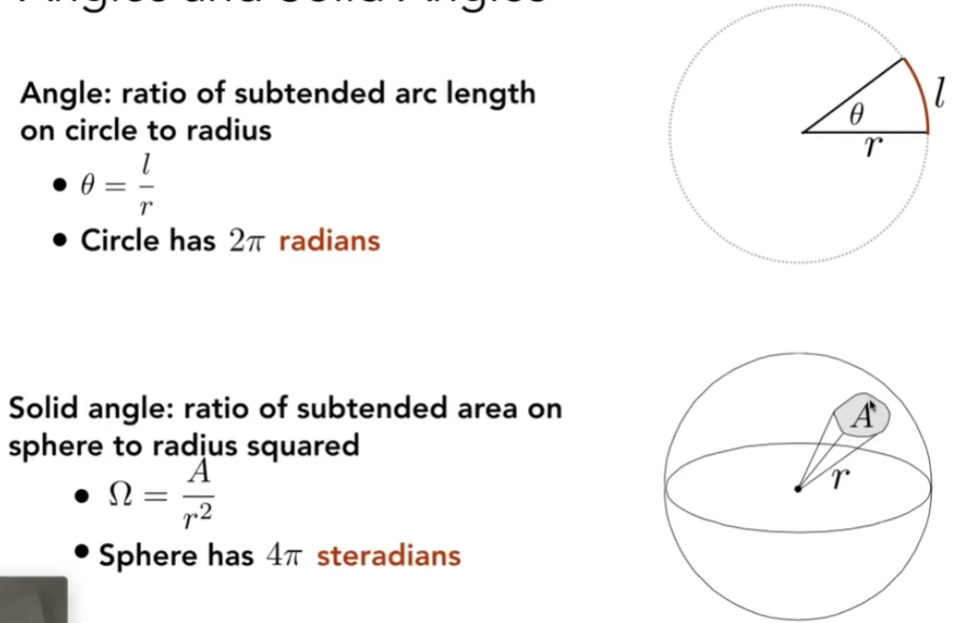
- 表示空间中的角有多大
- 可由二维的弧度表示角有多大来延伸
单位立体角 = 单位面积 / r2
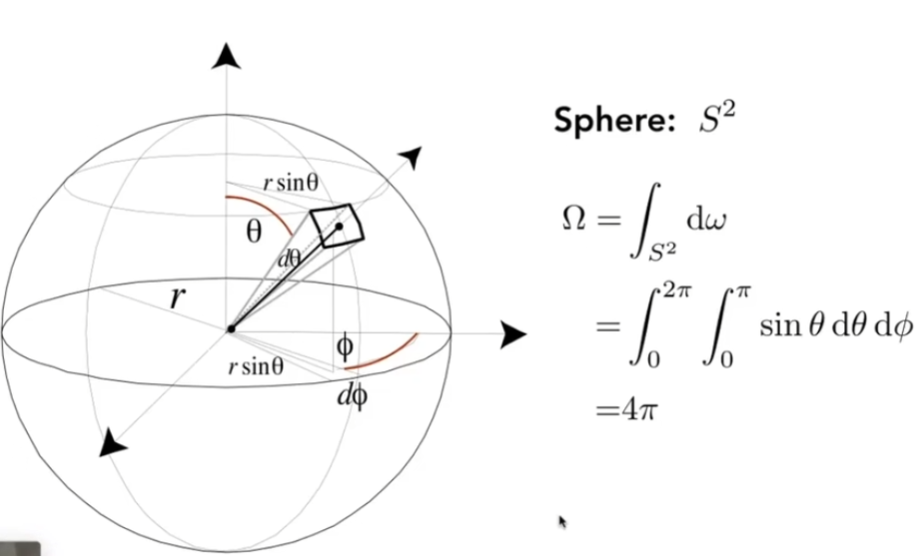
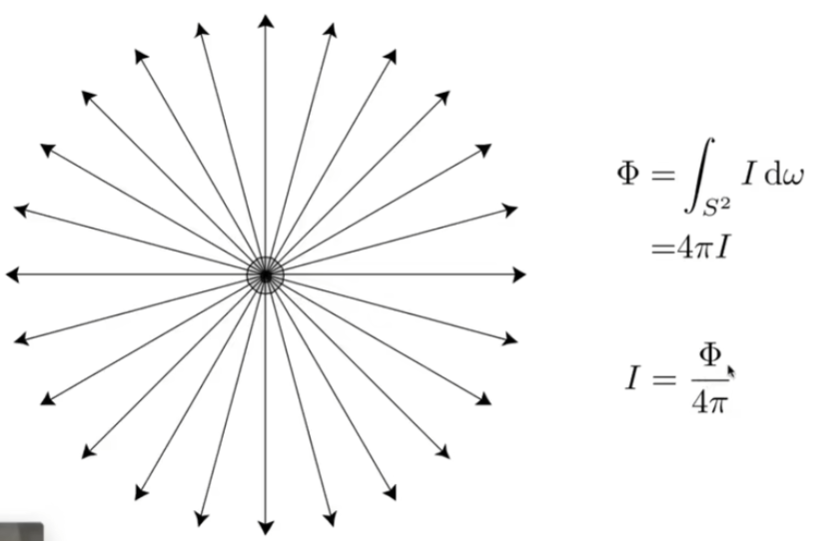
如果把球的所有方向对应的立体角积分起来,得到的是4π
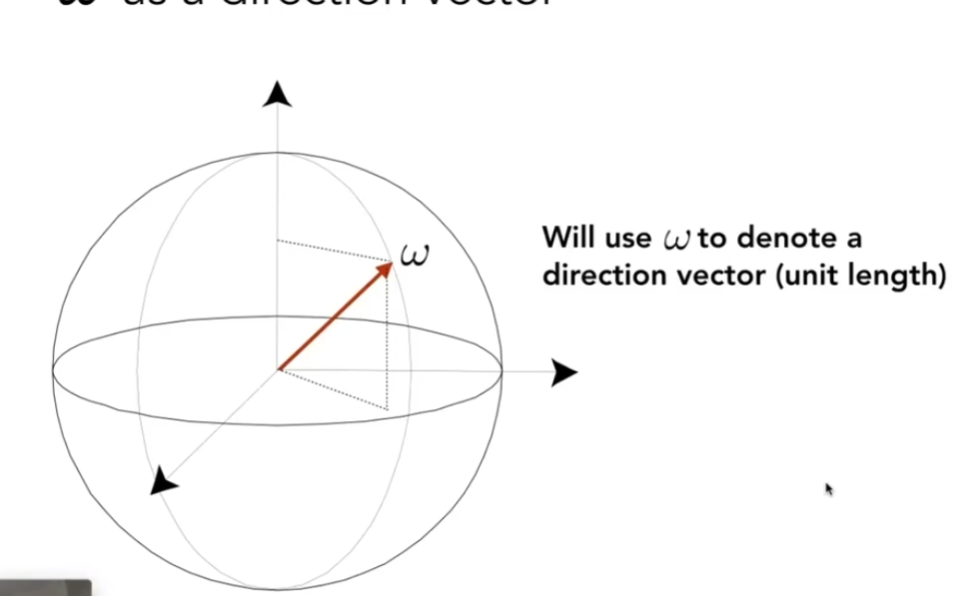
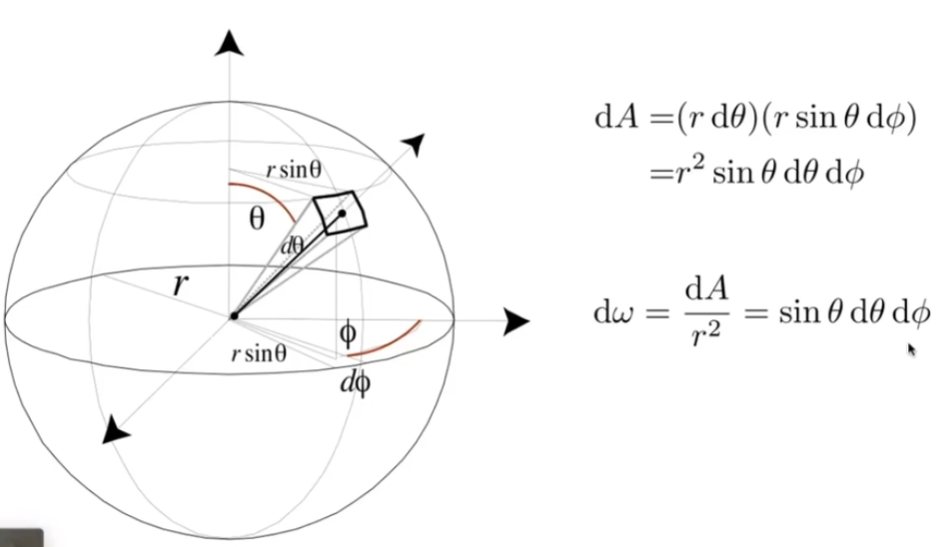
在辐射度量学中,用 ω 表示三维空间中的方向,可以用 θ 和 Φ 的方式定义它的位置,通过sinθdθdΦ算出单位立体角(微分立体角)是多少
回到Intensity的定义,其实就是光源在任何一个方向上的亮度(Flux或Power) / 对应单位立体角
既然Intensity = dΦ / dω ,反过来积分,把所有方向上的Intensity积分起来,一定能得到Power
如果一个点光源往各个方向均匀地辐射出光,那么任何一个方向上对应的Intensity = Power / 4π

实际例子:60瓦指看上去像60W的白炽灯,实际是11W,规格815流明
如果认为这个灯向四面八方辐射出的能量是一样的,则可以算任意方向的Intensity是多少
总结

- 光源总在不断辐射出能量,这个能量在图形学里很少用这个概念,比如太阳能板,接收光照时间越长,吸收能量越多
- 为了分析问题,一般考虑的是单位时间的能量,因此引入Radiant flux(power),对应灯泡的功率
- intensity就是在单位立体角上的能量
- 球体表面积的计算公式为 S = 4πr2
Lecture 15 Ray Tracing 3
Irradiance
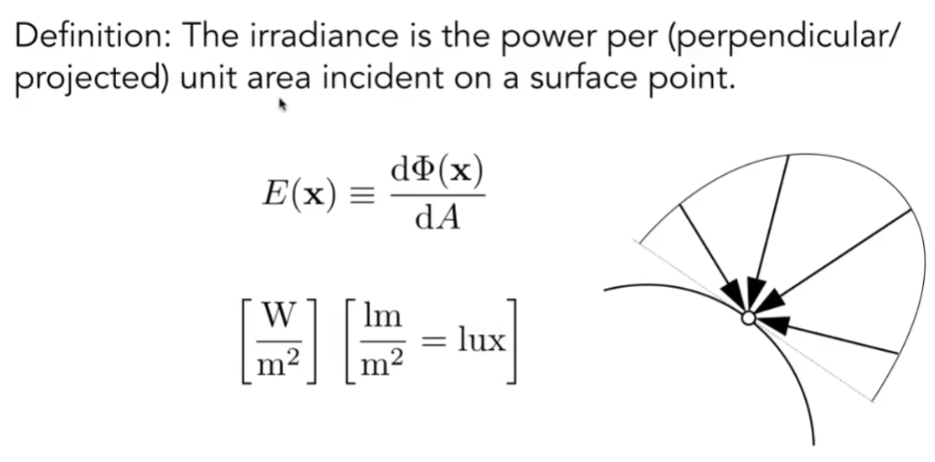
- 定义:Power per unit area
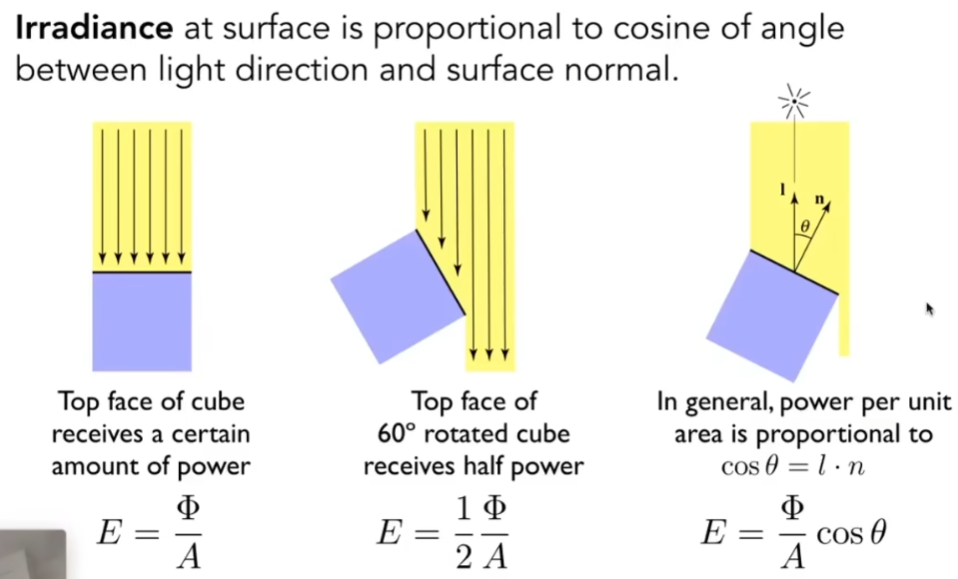
- unit area:面必须和光线垂直,如果不是垂直,通过投影变成垂直
- 之前说到Blinn-Phong点光源辐射出的能量到达着色点,和着色点本身的吸收,都有能量损失,而到达着色点有个r2的衰减,可以用Irradiance正确地解读

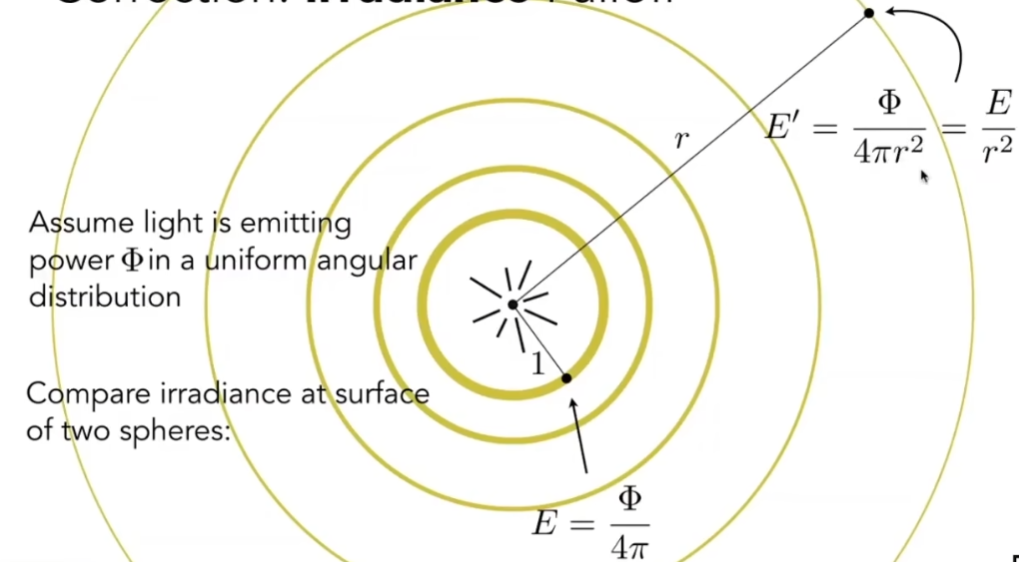
- 定义点光源power(功率)为Φ,认为往各个方向均等地辐射出能量
- 可以看出,变的是Irradiance,而不是Intensity(单位立体角上的能量)
Radiance
- 为了描述光线传播过程中的属性

- 定义:power在单位立体角,并且在单位面积上有多少
- 联系:

- Incident Radiance:
- 入射进来的能量

- Irradiance为dA收到的能量,Irradiance per solid angle是说这个能量要往某一个方向去辐射,能量本身会往各个方向辐射,但这个能量往这个方向去辐射,会辐射出多大的强度来
- 反过来理解,从一个方向,打到这个小的面上来,到达这个面的时候,应该会有一些能量,这个能量就是Irradiance。本身如果考虑来自四面八方的能量,可以得到dA总共收到多少能量,但只考虑从某个方向进来的能量被dA收到了多少,这个概念就是Radiance
- 所以Irradiance和Radiance的区别在于是否有方向性,考虑从一个方向进来,并且被dA收到的能量为Incident Radiance
- Exiting Radiance:
- 一个面发出去的能量

- 这个很小的面会往各个方向发出能量,dA往某一确定的方向(dω立体角)上去有多少的Intensity
- 对于Radiance,要考虑成两个部分,一部分是一个很小的面dA,一部分是一个很小的范围(无论是进来还是离开)
Irradiance vs. Radiance
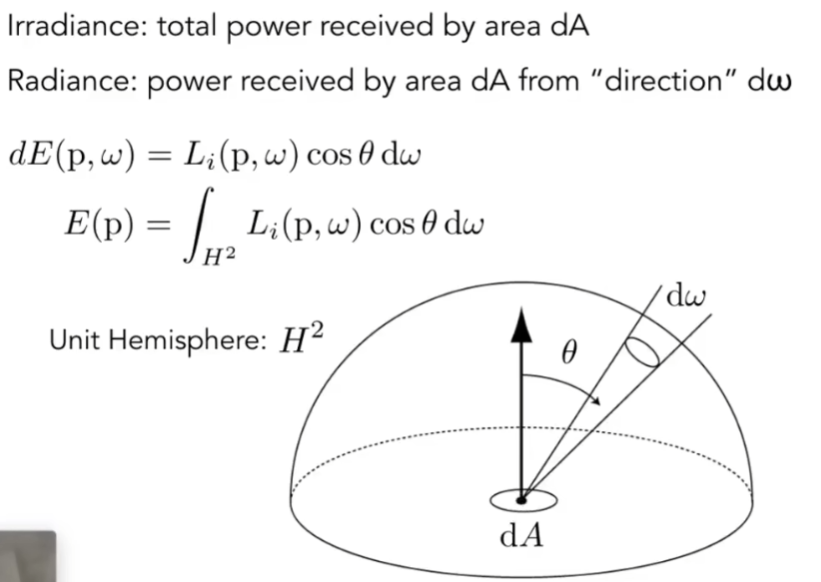
- Irradiance:dA(在某一小范围)收到的所有能量
- Radiance:还是看某一很小的范围,只考虑从某一方向进来,能让dA收到的能量
- Radiance无非是在Irradiance上加了一个方向性
- dA这么一个小的范围可以写成Irradiance形式(E(x)),某一方向Radiance是L,考虑朝向乘以cosθ,然后考虑立体角dω
- 从dω立体角来的所有能量,可以通过这种方式把Irradiance和Radiance联系起来
- 整理式子,两边分别积分,p点收到的所有能量,就是从每个方向过来的能量积分起来(积分就是求和)
Bidirectional Reflectance Distribution Function(BRDF 双向反射分布函数)
- 一个描述 光线打到漫反射物体后向四面八方反射 性质的函数:有多少能量,如果从某个方向进来,它会往不同的方向去,怎么样去分散,不同的反射方向上会分布多少能量
- 有两种理解反射的方式:
- 光进来后打到一个物体,改变一下方向,被弹走了
- 光线打到了某一物体表面,被吸收了,再从这个物体表面把这部分能量发出去,经过了一个中间过程
- 如果按后者理解,就可以用Irradiance和Radiance来解释反射
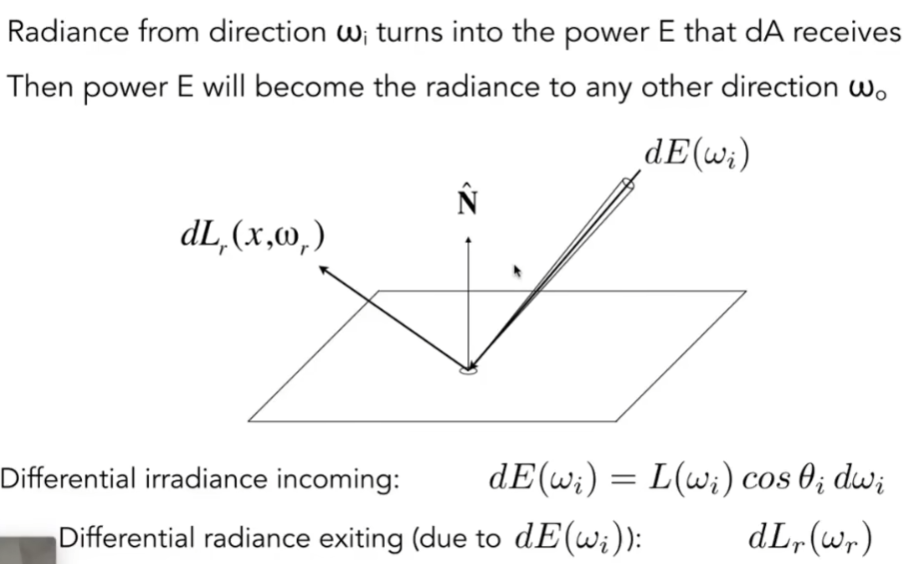
- 从 ωi 来的Radiance,会打到dA上,dA吸收了多少,然后再发出去
- 相当于入射的Radiance,会在dA处转化成power,这个power优惠辐射到另外一个方向去
- 所以通过这个能量,可以把入射和出射联系起来
- 考虑微小面积dA,从某一微小立体角 dωi ,接收到的Irradiance,会如何被分配到各个不同的立体角上去,这个分配比例,就是对于任何一个出射方向的radiance除以dA这么一小块接收到的Irradiance,就是BRDF的定义
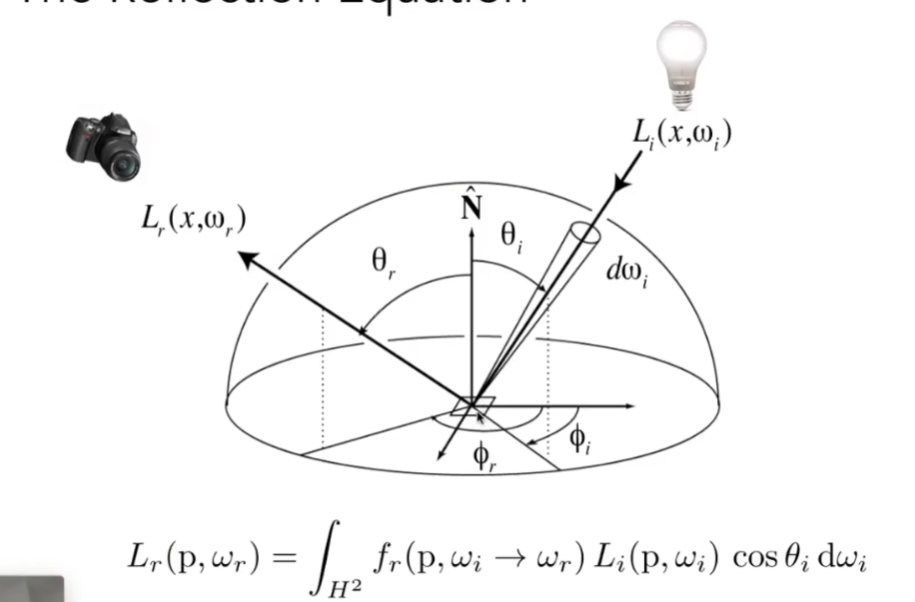
- 对于每一个入射方向,都会有对应入射方向——着色点——出射方向的BRDF,BRDF会告诉我们从某个方向进来的光反射到出射方向有多强,那就把每一个方向的入射光强度(radiance)乘以BRDF乘以cosθ,把每个方向对出射方向的贡献都加起来,就可以得到这个点在所有可能的入射光下,最后反射到出射方向上看过去是什么样的
反射方程和渲染方程

- 所有的光线传播都可以用这条公式(渲染方程)来总结
- 反射方程告诉我们,要从某个点观察某一个着色点,要考虑能够到达着色点的所有光线,这些光线不只是光源能够到达,如果有其他物体在,也会被照亮,也会反射出光
- 如果物体自己会发光,只要把自发光加上就可以
- 渲染方程跟Blinn-Phong着色模型一样,还是假设所有光线都朝外(明明是光线打进来,这里的ωi表示为朝向外的向量)
- (n·ωi)法线点乘入射方向,就是cosθ
- dωi指考虑所有可能的入射方向,指从球心向各个方向去
- Ω+指半球,因为只考虑半球的话,法线朝上,如果光线从半球下打过来,认为对反射的贡献为0
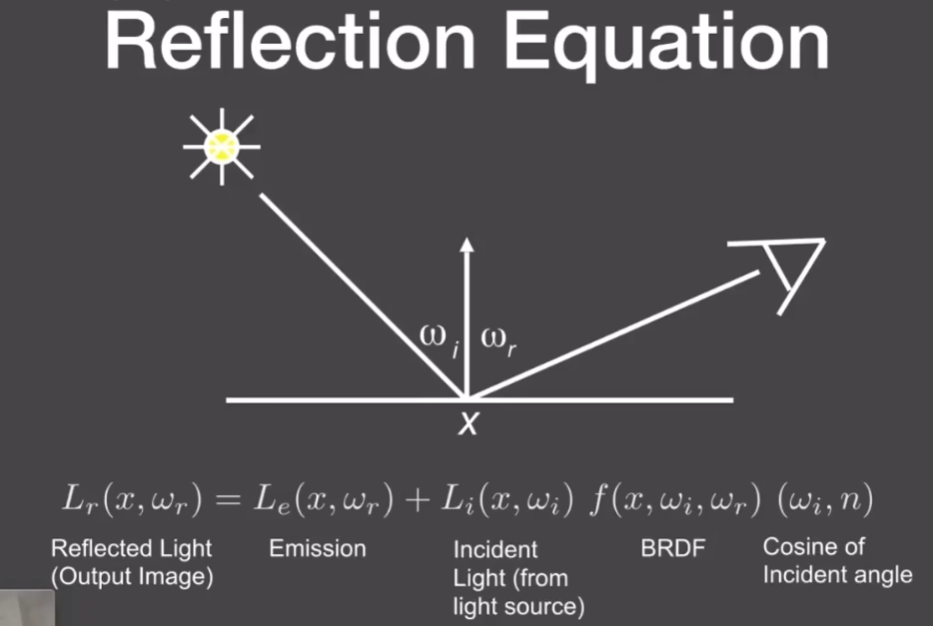
- 一个点光源下的反射方程
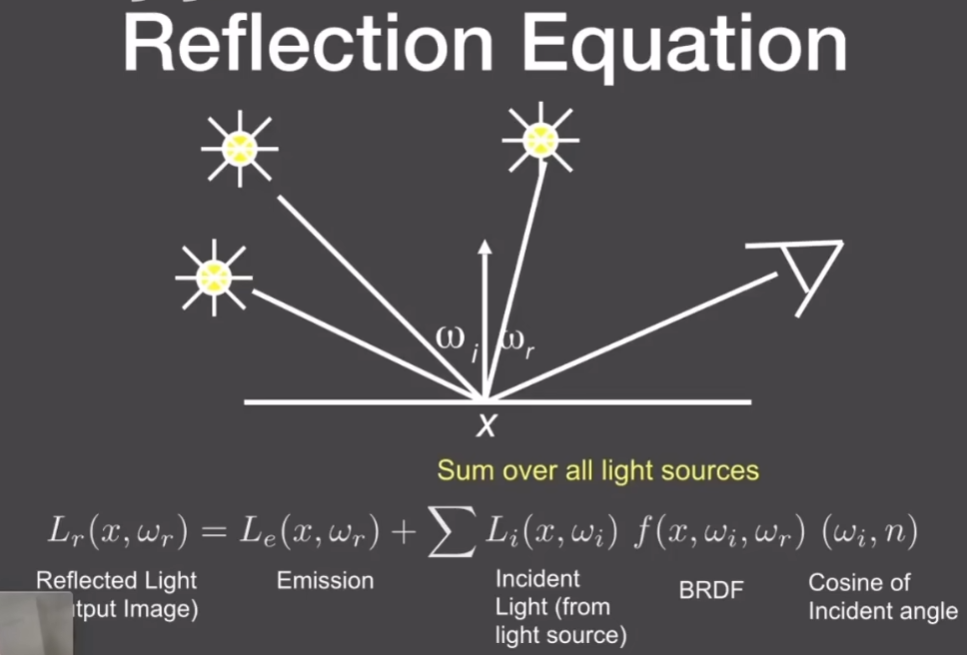
- 多个点光源,就把每个点光源的贡献加起来
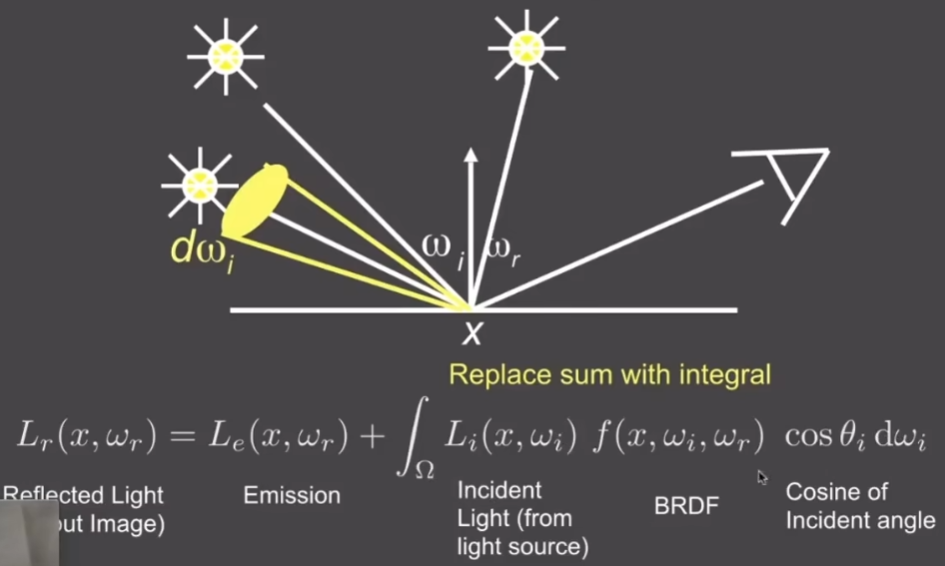
- 如果有面光源,把面光源理解为一堆点光源的集合,以前可以把所有点光源加起来,那么也可以把面光源上任意点光源积分起来,积分这个面光源所占据的立体角,考虑所有覆盖的方向,从这个方向来的Radiance经过BRDF反射过去应该是什么样的Radiance出去
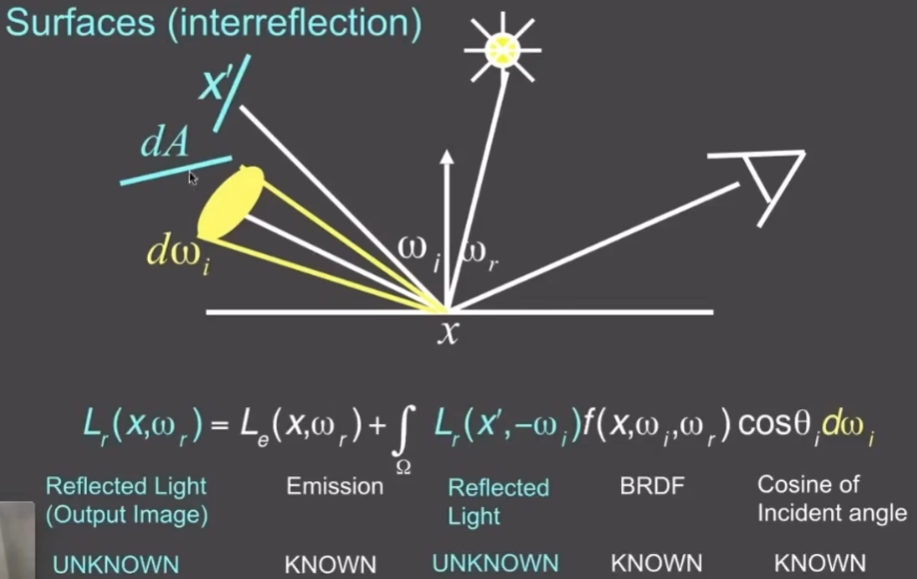
- 如果有其他物体反射来的Radiance,就考虑这些物体反射出去,并且正好回照亮x点的Radiance是多少,相当于把物体当成是光源

- 在数学上有简单的表达方式
- 两个不同的位置,用u、v表示
- l为辐射出去的Radiance
- e(u)为着色点自身发出去的能量
- 加上从其他的物体表面,通过BRDF,把从其他物体表面来的Radiance反射到当前着色点位置上,会有多大的能量反射到观察方向上
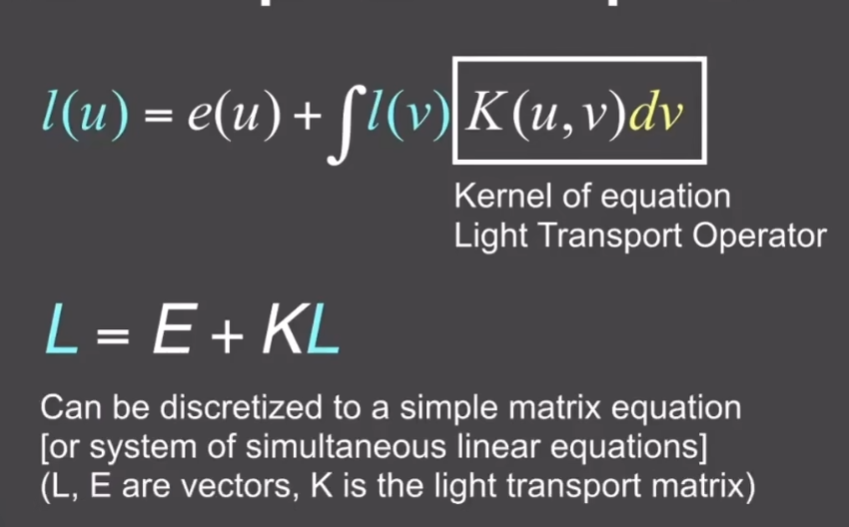
- 可以进一步简写,把BRDF连着积分的东西都写成某种操作符
- 所有物体辐射出的所有能量 = 光源辐射出的能量 + 辐射出的能量被反射后的能量
- 目的是为了解渲染方程

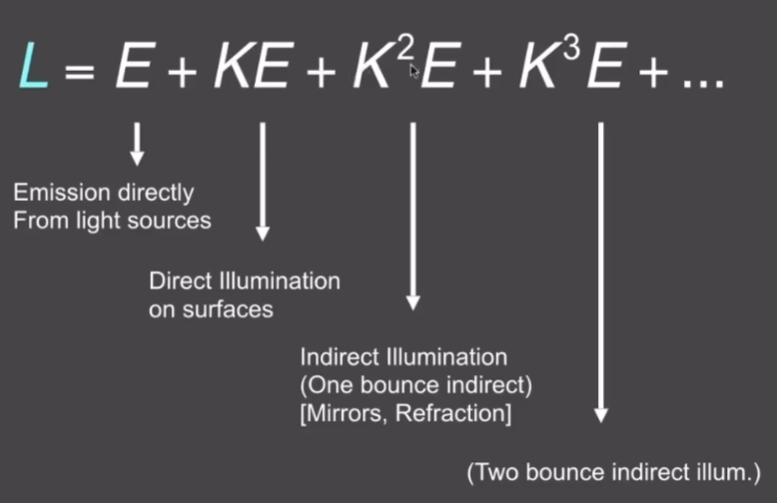
- 最后可以经过泰勒展开得到不同弹射次数的分解
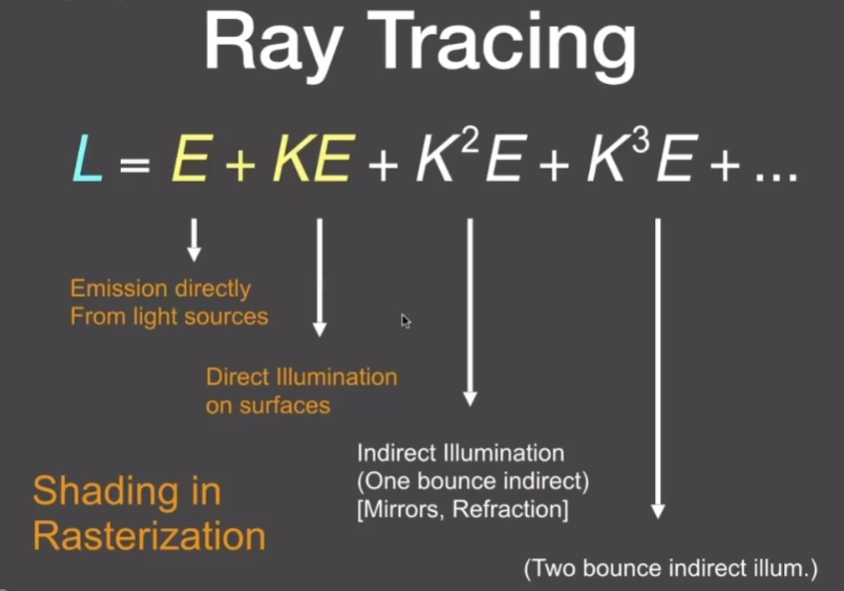
- 从另一个角度来理解
- 光栅化可以把物体投影到屏幕上,已知屏幕上任何一着色点的位置和光源位置可以做着色,着色做的就是直接光照,光源自己可以直接投射到屏幕上来(可见的话)
- 光栅化做的就是0次和一次光线弹射的部分,后面的部分比较难做,这就是光线追踪要做的部分,就是间接光照
概率论回顾

- 随机变量、概率分布
- 随机变量会以不同的概率取不同的值
- 满足:所有概率都是非负的、所有的概率相加为1

- 期望:不断地去取随机变量,求它们的平均

- 在连续的情况下描述概率和它的分布
- 概率密度函数(PDF):在某一点x取它周围的微点dx,向上连线,与曲线和坐标轴围成的近似梯形区域的面积为该点x对应的概率,这条曲线叫做概率密度函数

- 求期望就是把值乘以概率密度并且积起来
Lecture 16 Ray Tracing 4
Monte Carlo Integration(蒙特卡洛积分)
- 是一个求定积分的方法,最后得到的是一个数(围成的面积)
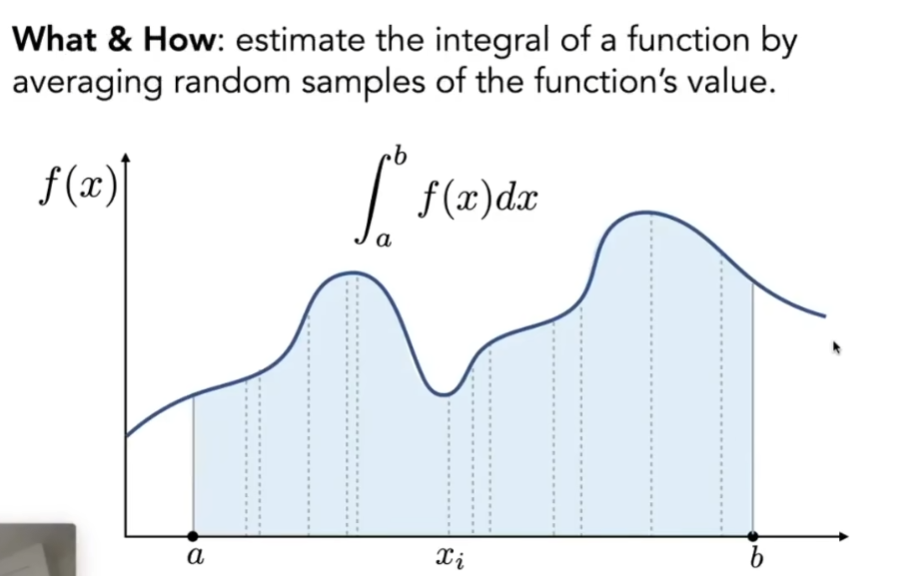
- 回顾黎曼积分的做法,是把ab之间均匀地拆成多份,每一份取中间位置,找到对应的y,认为每一份都是一个微小的长方形,把整个曲线下方的面积分解成各个不同的小正方形的面积之和
- 蒙特卡洛积分,是一种随机采样的方法,在ab间重复采样多次,每次采样到xi,找到对应的f(x),得到对应长方形的面积,采样多次,将得到的面积平均起来

- 已知任何一个采样点的函数值,已知概率密度
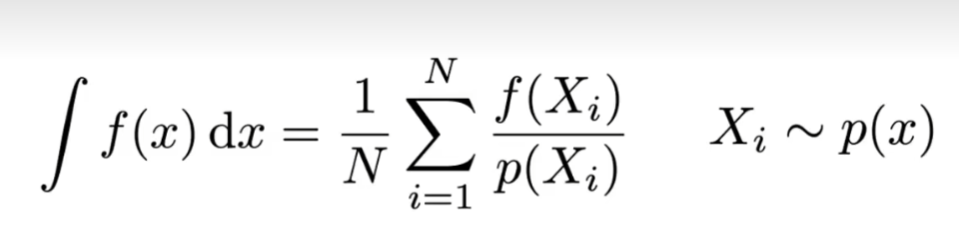
- 只需要在积分域上,以一定的PDF进行采样,对每个样本,算f(X)/p(X),最后平均起来
- 采样点越多,误差越小
- 不用考虑积分域,已经在PDF里体现了
- 要求只能用积分域上的点做蒙特卡洛的积分近似(在x上积分只能用x,其他变量不成立)
Path Tracing(路径追踪)
为了解决Whitted-style ray tracing中非基于物理的、不正确的问题
Whitted-style ray tracing的做法:
- 不断地弹射光线,在任何一个位置都和光源连一条线
- 当光线打到光滑的物体上,会沿着镜面方向反射、折射方向折射;当打到漫反射物体,就不再弹射
Whitted-style ray tracing的问题:

- 如果对于Glossy的材质,还沿镜面方向反射,是不对的

- 打到漫反射物体后就停了
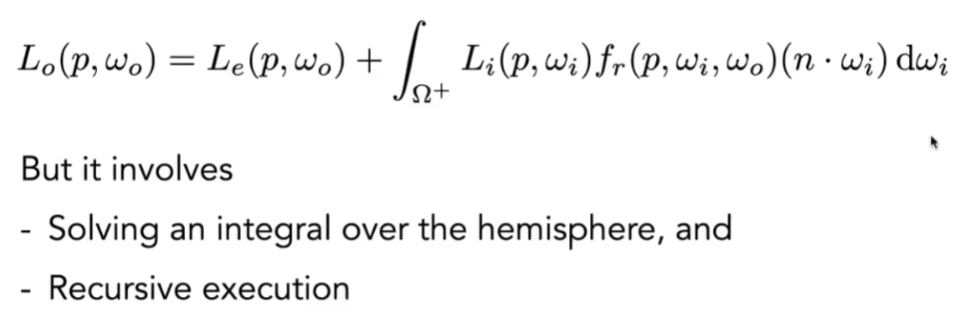
- 既然Whitted-style ray tracing是错误的,而渲染方程是正确的,那么就要正确地解出渲染方程,要考虑两个问题:
- 它本身是积分,对半球内四面八方来的光线
- 本身也是递归的定义,解这个点的渲染方程,同时要解从其他地方来的光线的渲染方程


- 第一个问题用蒙特卡洛积分
- 只考虑直接光照

- 对着色点p,出射方向ωo,要算四面八方的光源对这个点的直接光照贡献,可以写成这个算法
- 从这个着色点,往半球上发出N个不同的方向采样,按照某种PDF
- 初始化结果为0
- 对任何一个选中的方向,从p点往这个方向连出一条方向
- 如果这根光线打到了光源,就把求和式子写出来,自然能知道光源的辐射(Radiance)L_i,BRDF f_r也知道,cos也知道,pdf(wi)是均匀采样的PDF
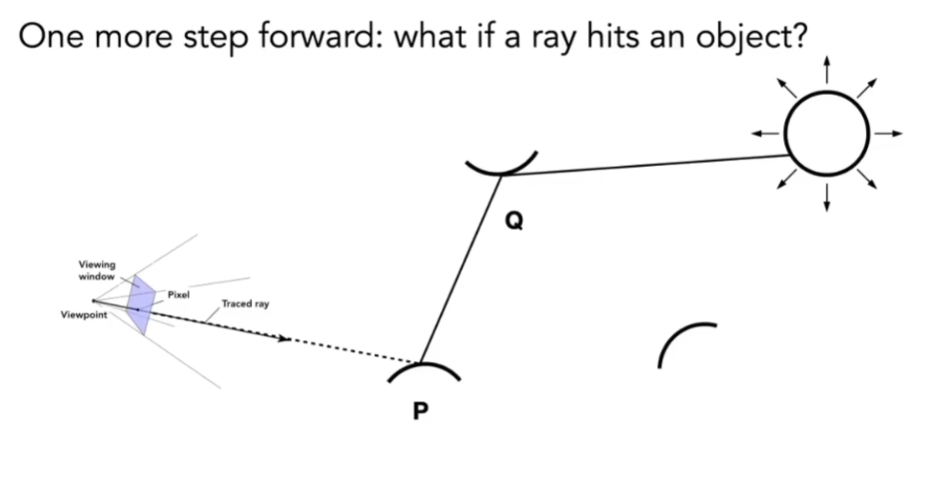
- 引入间接光照
- 从Q点到P点的Radiance,可以看成Q点也是个光源
- 可以类比P点是摄像机,从P点去观察Q点,算Q点的直接光照一样

- 把Q点的直接光照的结果,作为Q点过来的光照
- 此时仍有几个问题:
- 光线的数量会爆炸 #rays = N#bounces;递归没有停止条件
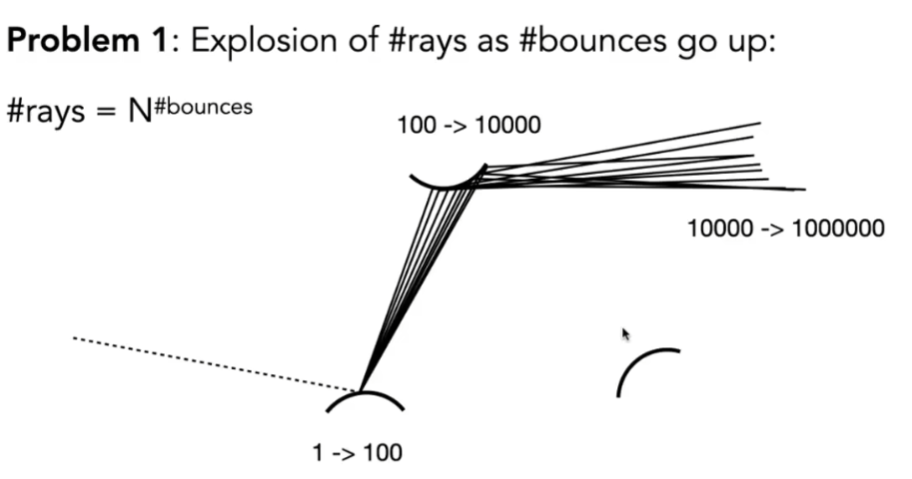
- 只有N = 1的情况下,才不会爆炸

- 修改:随机往一个方向采样
- N = 1时,这种方法称做路径追踪;N != 1时,称做分布式光线追踪
- 光线的数量会爆炸 #rays = N#bounces;递归没有停止条件
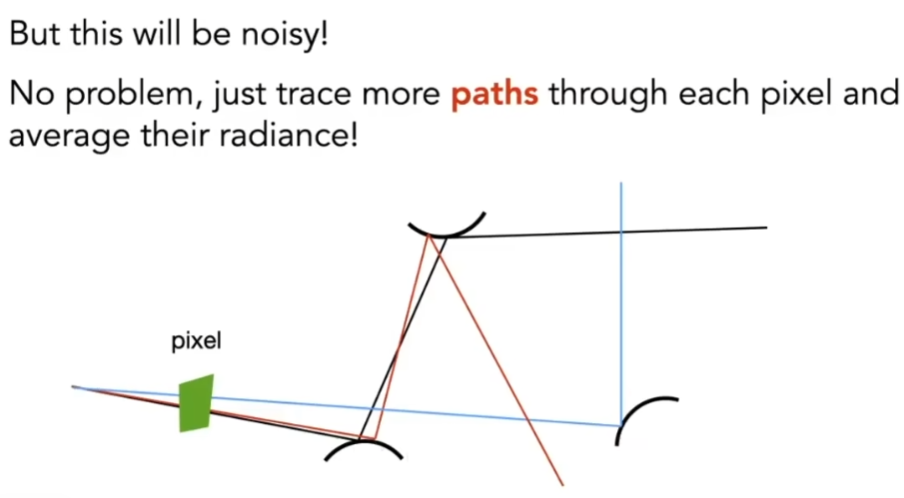
- 当只考虑一条光线时,噪声非常大
- 最后要的是像素的Radiance,而穿过这个像素会有很多不同的路径,最后像素是多少,由所有路径求平均,只要有足够的的路径就可以了
- 每个像素,发出一系列光线,在任何一个打到的点上,把着色的结果求平均算出来

- 在像素内均匀地取某一位置
- 对任一选取的位置,从视点连一条光线到样本的位置,如果这根光线打到场景中某个位置,就算这一点的着色

- 为了解决第二个问题,不能设置递归条件为光线弹射几次,因为总会损失能量,而引入俄罗斯轮盘赌的方法来决定以一定的概率来停止继续往下追踪

- 积分的结果需要算出来等于Lo
- 以一定的概率(提前定好)P,往某一方向打一条光线,得到一定的结果后,除以P作为返回值
- 以另外的一部分概率 1 - P内,不打光线,得到结果为0
- 最后的期望仍然是Lo

- 代码上修改极少
- 定义某一概率P_RR,每次选取[0, 1]间的数ksi

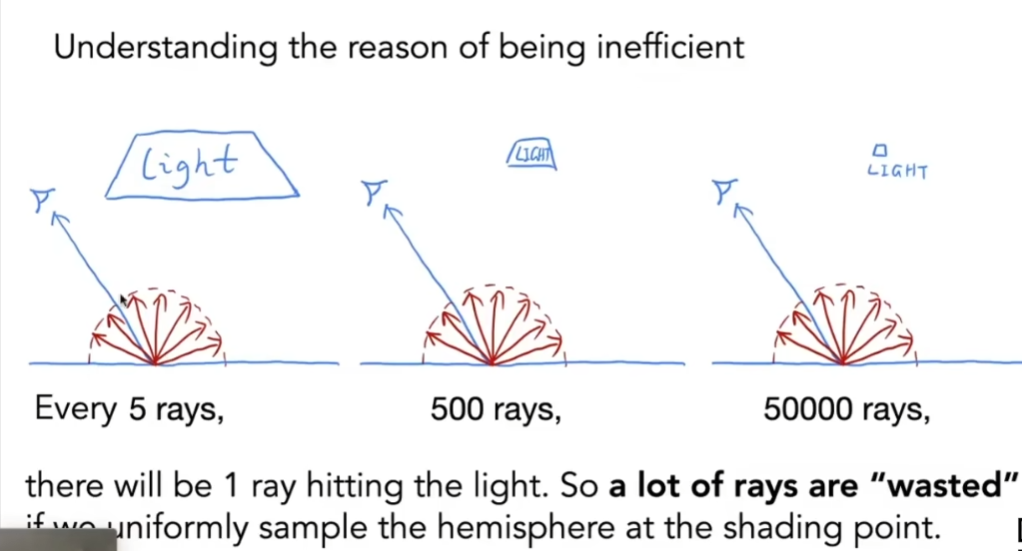
- PDF如果均匀地往四面八方采样,可能会有很多光线浪费,于是考虑直接在光源上采样

- 如果想采样光源,将光源理解为二维的框,在这个平面上均匀采样,所用的PDF是 1 / A
- 而渲染方程不是定义在光源上的,它是定义在立体角上的积分,定义在半球上的
- 蒙特卡洛要求在x上积分就要从x上采样,从光源上采样,就得把渲染方程写成对光源上微表面的面积进行积分,只需要知道dω和dA的关系
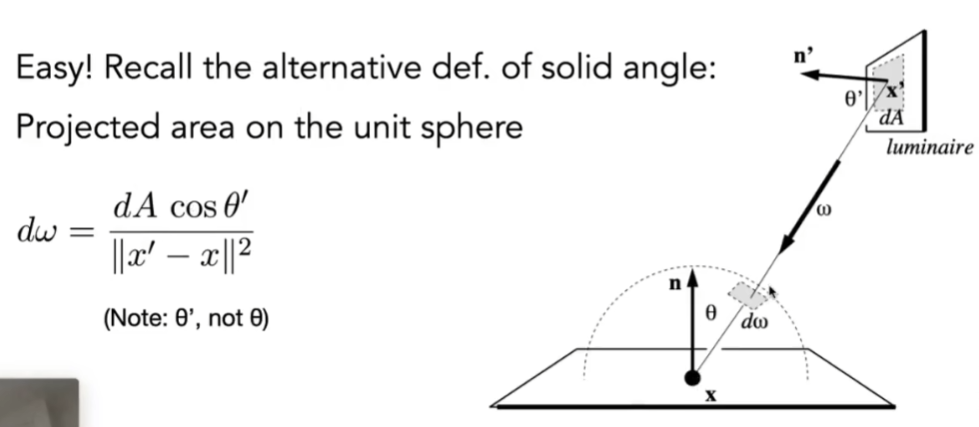
- dω是dA投影到单位球上的立体角,立体角是空间面积除以距离平方
- 按照立体角的定义,先把面朝向着色点,再除以距离平方
- 重写渲染方程:


- 现在,将光线传播拆成两部分:
- 光源直接对着色点的贡献
- 所有其他非光源的贡献


- 最后考虑光线传播过程中是否有遮挡



Lecture 17 Material and Appearances
Material
- 在渲染方程中,BRDF是决定材质的,材质是BRDF的一个参数
反射
- 漫反射系数定义:
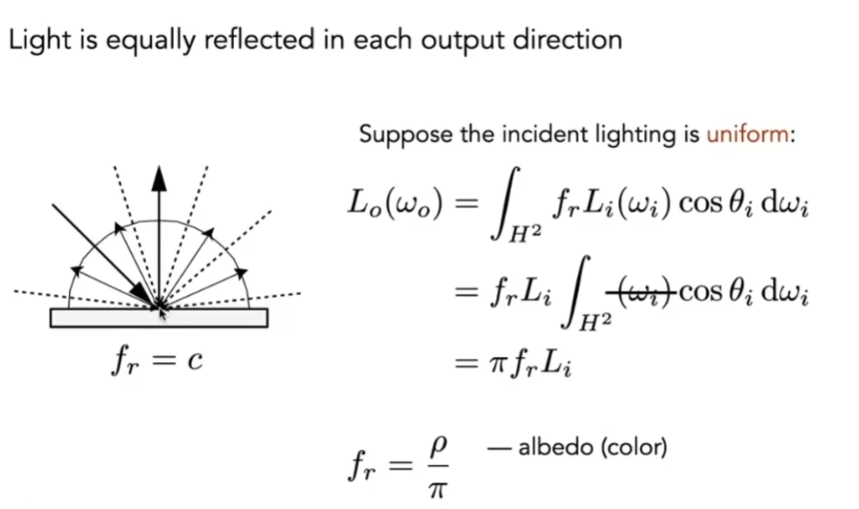
- 首先,材质是漫反射材质
- 任何的光线进来,都会被均匀地反射出去
- 认为从空间中任何一个进来的光线的Radiance都是一样的
- 利用能量守恒,如果这一点不发光,也不吸收光,也就意味着所有的能量进来多少,就反射多少
- 观察到入射光是均匀的uniform的,入射和出射的Irradiance相同,则入射光的Radiance和出射光的Radiance也得是一样的
- 在渲染方程中,没有自发光项,认为入射光ωi从任一方向来,通过漫反射BRDF,会被反射到ωo上去
- 可以简化一下,因为入射Radiance和BRDF的diffuse是常数,可以拿出去,剩下的是半球上一个对cos函数的积分
- 半球上直接对立体角积分得到的是2π,而 Li = Lo ,可以得到 BRDF = 1 / π
- 如果BRDF = 1 / π ,这个时候,就是完全不吸收能量的BRDF
- 这时可以定义一个反射率albedo,可以是单通道的一个数,也可以是三个数rgb,也可以是光图,albeddo在[0, 1]之间,可以引入不同颜色的BRDF,这个BRDF的值就是albedo / π


- 反射公式有两种不同的理解方式:
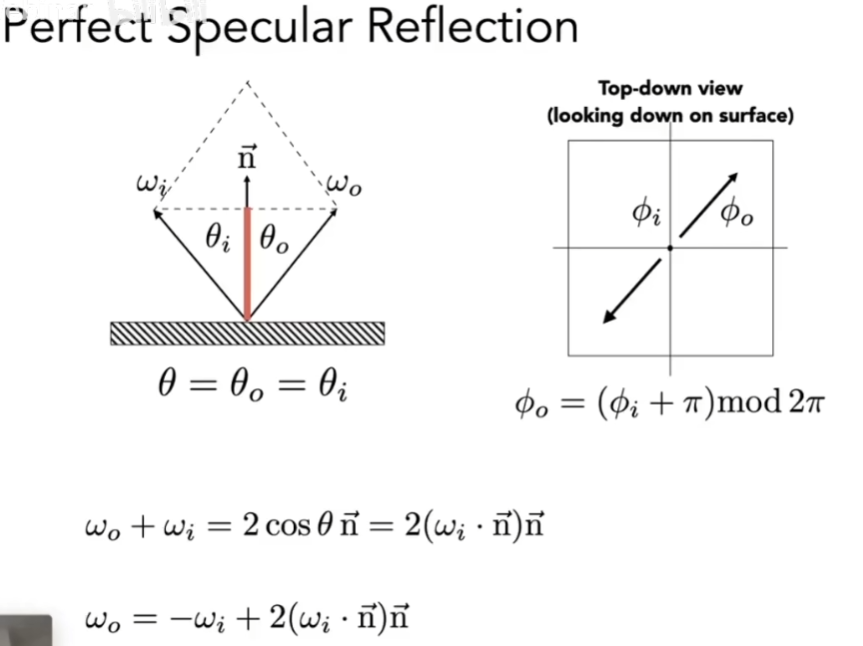
- 方法一:平行四边形法则,给定入射光和法线算出出射光
- 方法二:把这些角度投影到一个局部坐标系上
- 认为任何一个方向和法线的夹角(仰角),如θ = 0为沿着法线方向
- 定义一个Φ角,规定在某一个平面上,比如ion,认为Φ = 0,如果这个平面绕着n转动,引起的角度Φ
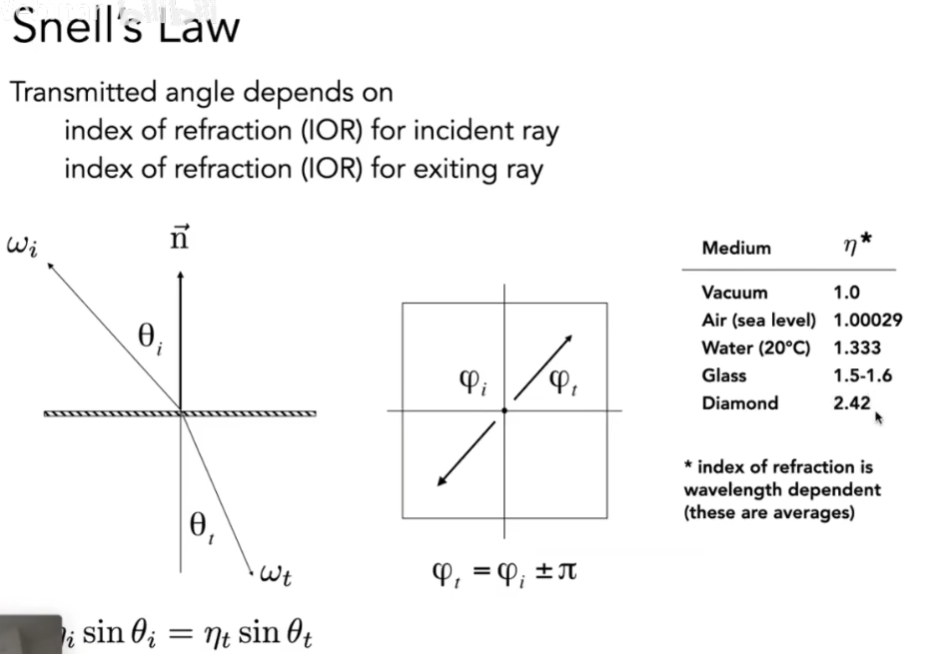
折射
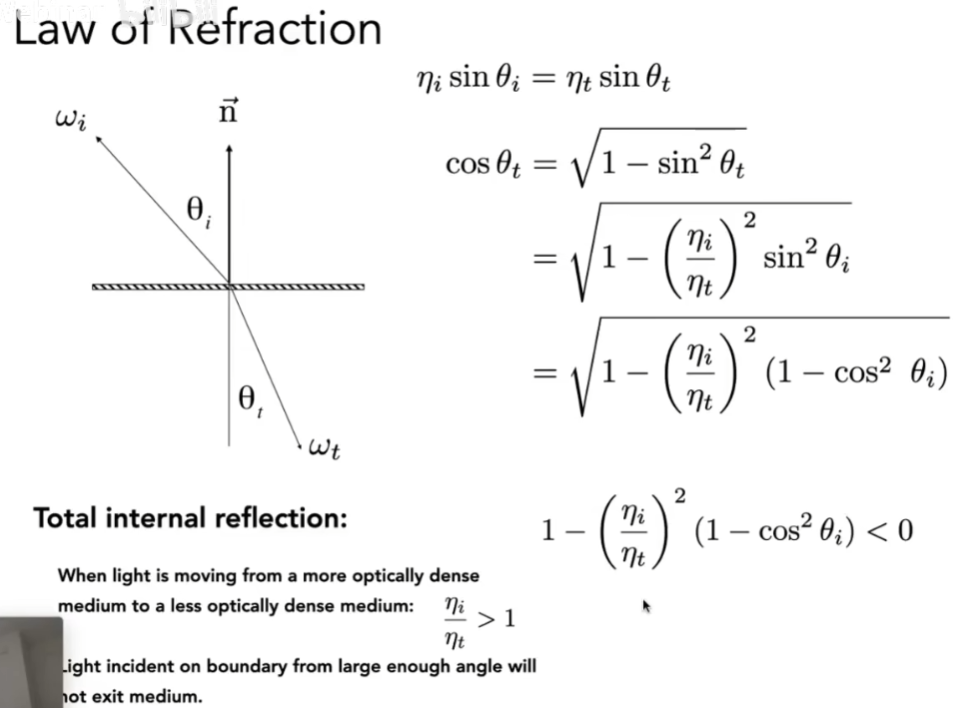
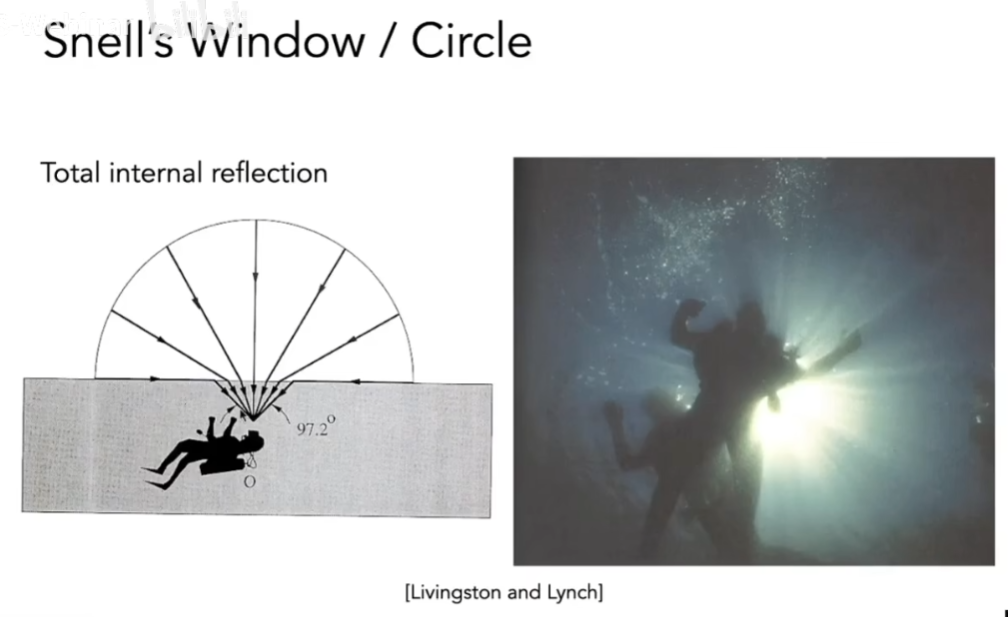
- 当入射的介质反射率>出射的介质反射率时,可能出现没有折射的现象,这个现象称为全反射现象

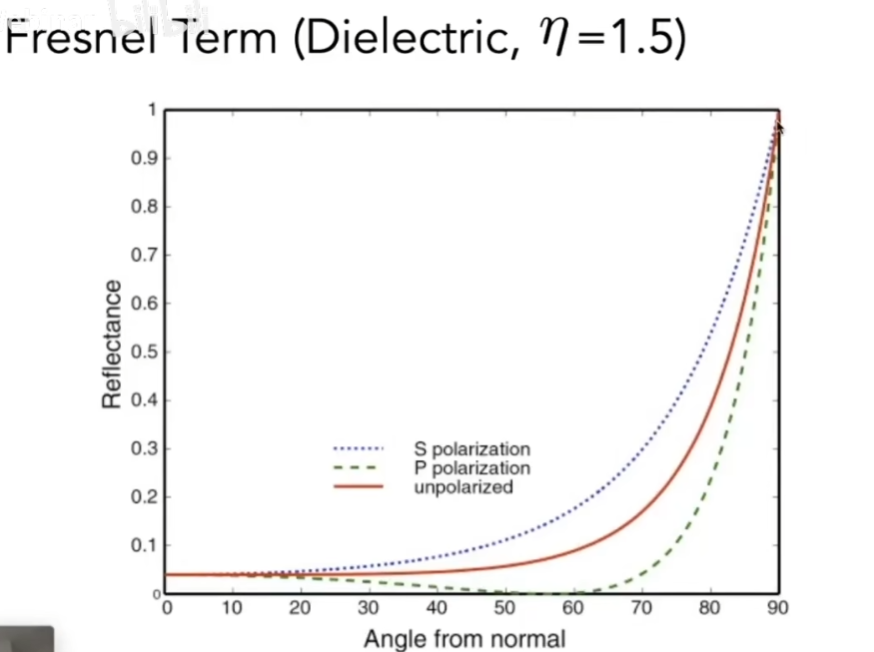
- 红线是菲涅尔项,告诉我们如果一根光几乎和物体表面完全平行,就会完全被反射;如果是垂直的,更多能量会直接穿过去发生折射,反射的能量非常少
- 另外两条表示极化性质,和光线的波动性有关,光线其实是沿着各个不同方向振动的,极化值只沿着S和P方向振动,正常情况下认为S和P方向都有振动,基本是两个方向上的平均,目前也没有什么渲染器在考虑极化的光的情况
- 这是反应了对绝缘体的菲涅尔项,对于导体又是另外一种现象
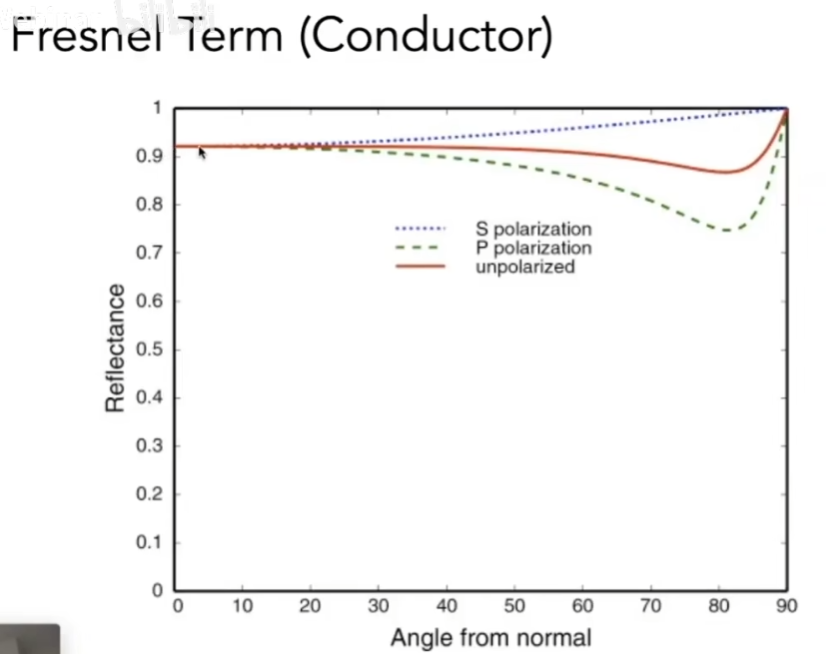
- 对于金属(导体)来说,它的菲涅尔项在任何情况下反射率都挺高的

- 菲涅尔项的计算可以简化,认为某一条曲线从某一地方开始,,0°的时候是某一个值,涨到90°的时候涨到1,拟合出一条曲线。它的基准反射率(在0°时的反射率,垂直入射的反射率)是和它们两个折射率是有关系的
- 不管对绝缘体还是导体,都可以近似地表达
Microfacet Material(微表面材质/模型)
- 真正的基于物理的材质

- 微表面模型:当离得足够远看向一个物体的时候,很多微小的东西看不到,看到的是它们最终形成的,光对表面的作用

- 微表面模型认为:从远处看,看到的是材质/外观,从近处看,是几何
- 每一个微表面认为是一个微小的镜面,每一个微表面都有自己的朝向(法线)
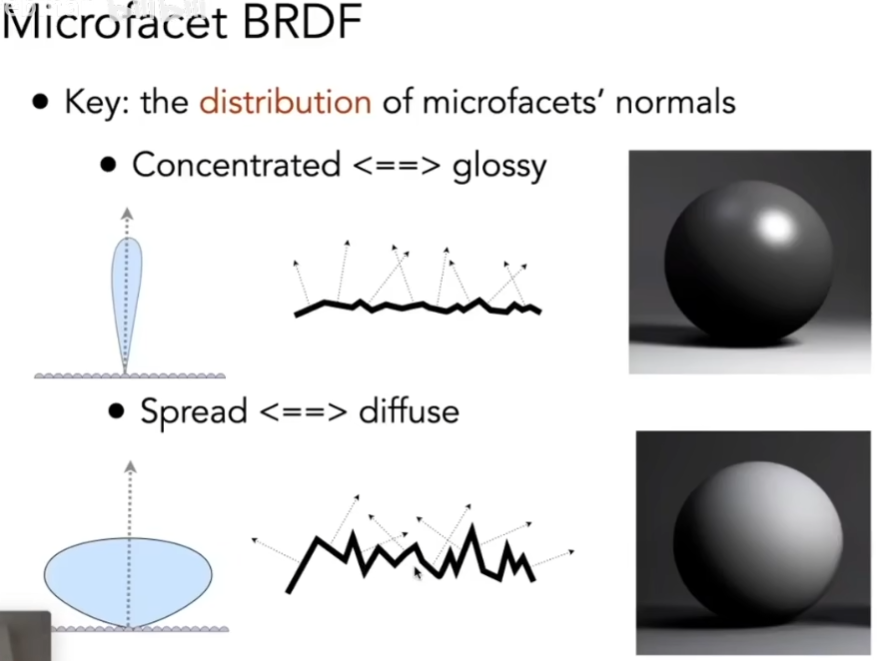
- 可以研究这些微表面本身法线形成的分布
- 可以把表面的粗糙程度用微表面的法线分布来表示,集中就是glossy,分散就是diffuse
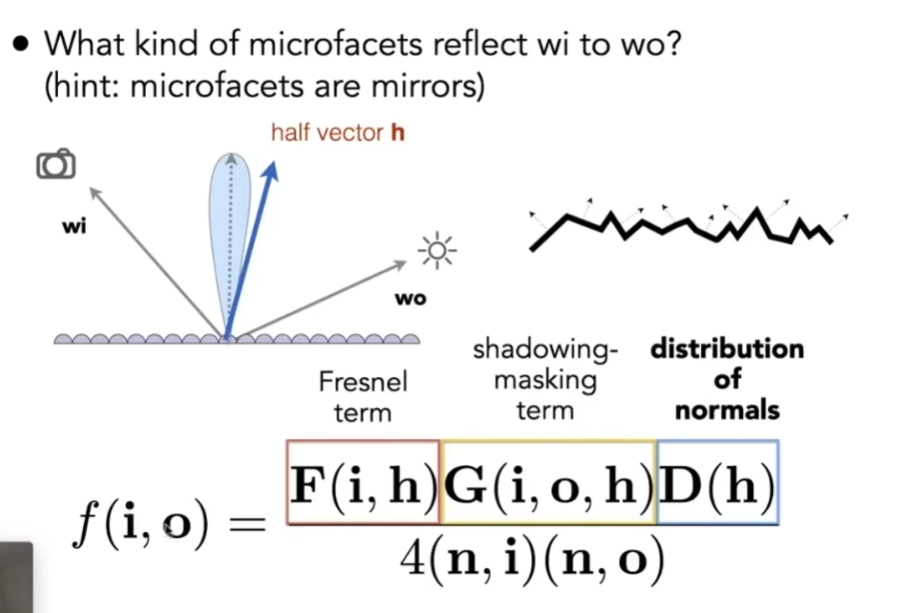
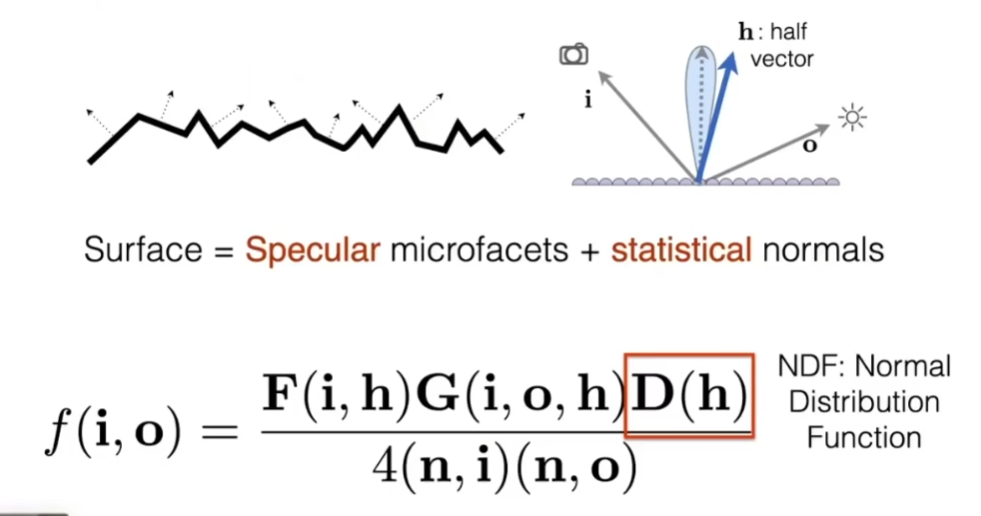
- 考虑菲涅尔项F、法线分布D、几何项G
- D:表示在任何方向上分布的值是多少,只有当法线方向和half vector完全一致的时候,微表面能够把入射方向的光反射到出射方向。微表面被认为是完全的镜子。查询在所有的分布里,有多少微表面的法线方向是沿着half vector方向去的
- G:修正微表面互相遮挡的情况,光线方向或观察方向只要接近Grazing Angle(接近水平),会发生遮挡
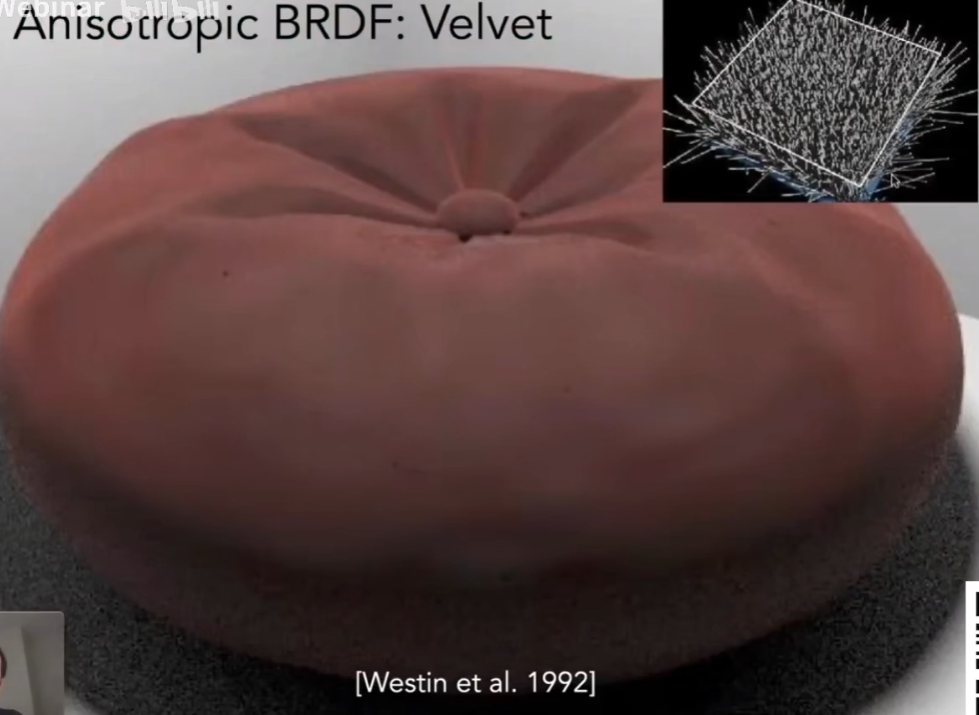
Isotropic / Anisotropic Materials
- 各项同性材质/各项异性材质

- 各项同性:认为微表面并不存在一定的方向性

- 各项异性:如果在BRDF上不满足在方位角上旋转,得到的还是相同的BRDF,就把它叫做各向异性的材质
- 其他各项异性材质例子:


BRDF的性质
- 非负性
- 线性性
- 可以拆成很多块,最后加起来算结果
- 可逆性
- 交互入射方向和出射方向得到的结果相同
- 能量守恒性
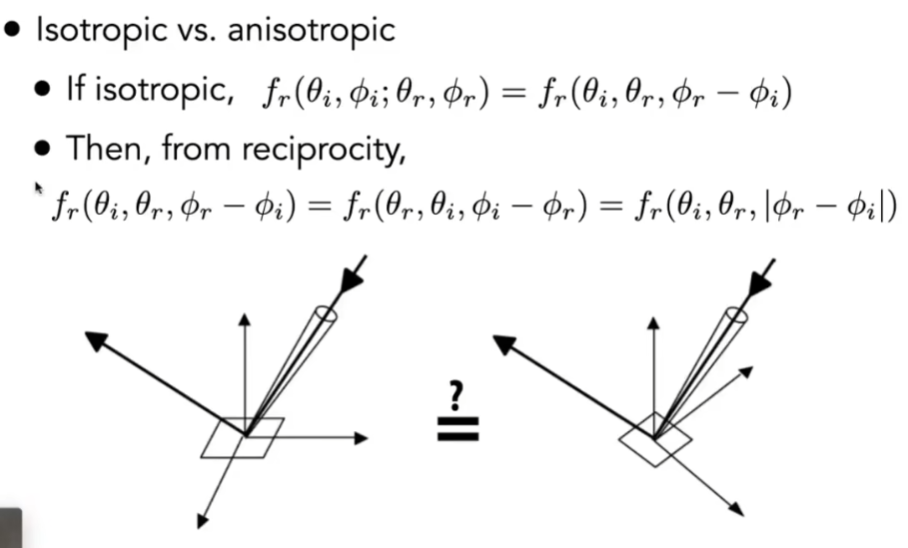
- 各向同性的话意味着BRDF的值只和相对的方位角有关,原本四维的BRDF可以变为三维的
- 根据可逆性,所有的BRDF,方位角不用考虑正负
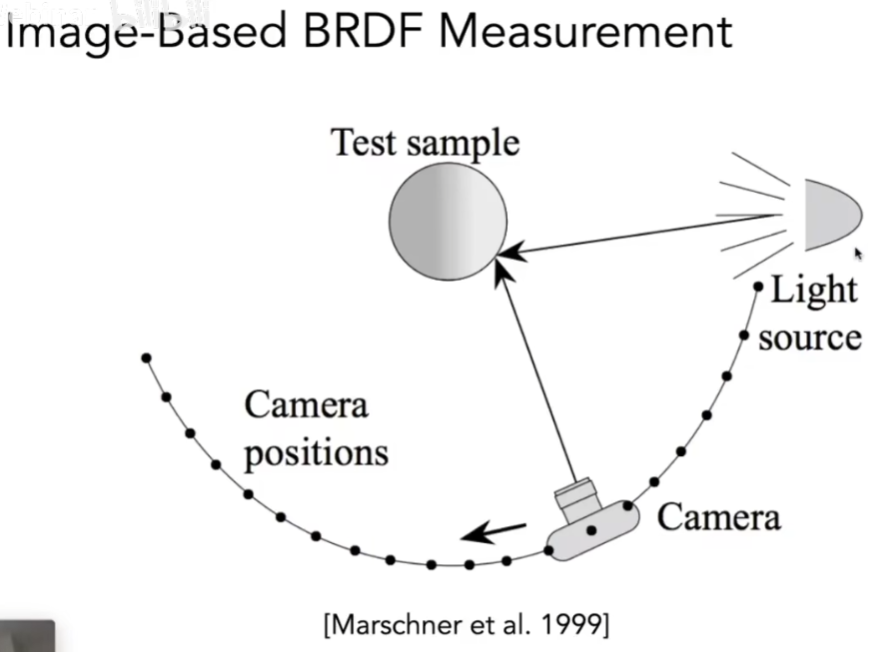
测量BRDF




Lecture 18 Advanced Topics in Rendering
Advanced Light Transport

有偏/无偏的光线追踪
- 做光线追踪很多的都是在用蒙特卡洛估计
- 无偏的蒙特卡洛:估计出的结果的期望永远都是对的
- 有偏的蒙特卡洛:所有其他情况。但如果用的样本足够多,在极限的情况下,期望值会收敛到正确值,这时还是有偏的,也是一致的(consistent)
双向路径追踪(BDPT)

- 思想:生成两个不同的半路径(子路径),把半路径的端点连起来,形成整个路径

- BDPT在某些情况下,效果会更好
- BDPT实现难度高,运行速度也慢很多
Metropolis(人名) 光线传播(MLT)

- 思想:用统计学上的一个采样工具,Markov Chain(马尔科夫链)
- 相当于当前有一个样本,马尔科夫链可以根据当前样本生成一个跟它靠近的下一个样本
- 好处:它可以做到,给定足够的时间,马尔科夫链的蒙特卡洛方法(MCMC)可以生成一系列以任意函数的形状为PDF的样本。当采样的PDF和要积分的函数形状一致的时候,得到的效果是最好的,而任何未知的函数用马尔科夫链的办法能让生成的样本分布和被积函数形状一致

- 特别适合做复杂的场景

- 但不能估计什么时候收敛
- 所有操作都是局部的,有些像素收敛快,有些慢,使得图像看上去很脏,所以也不能用于做动画,前后两帧收敛不同,会强烈抖动
Photon Mapping(光子映射)

- 非常适合渲染caustics(国内翻译成”焦散”),caustics指由于光线的聚焦产生非常强的图案
- 光子映射的实现方法有很多
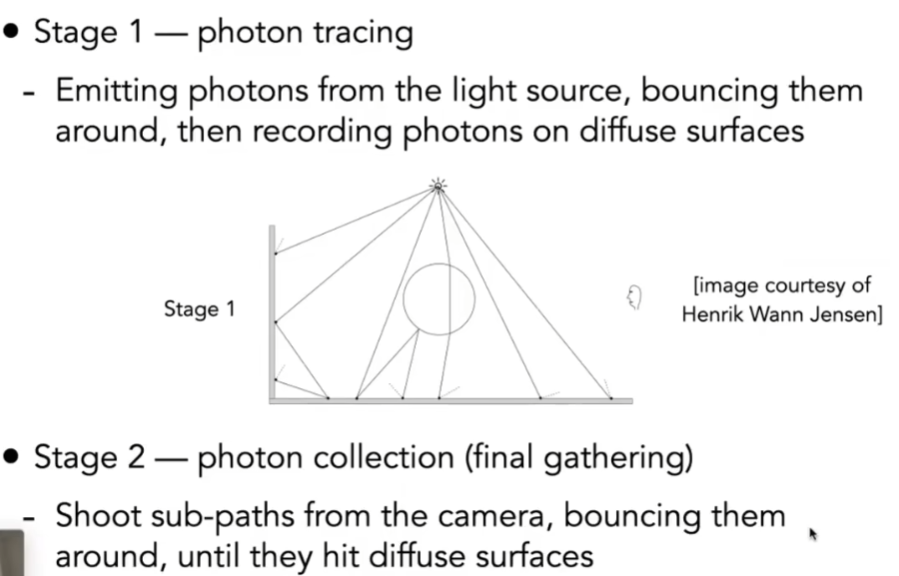
- 其中一种做法有两步
- 第一步:从光源出发,打出很多光子,该反射的反射、该折射的折射,直到打到漫反射物体停止(把所有光子记录到Diffuse物体上)
- 第二步:从摄像机出发,往各个方向打,会反射和折射,直到打到漫反射物体停止(也停在Diffuse物体上)
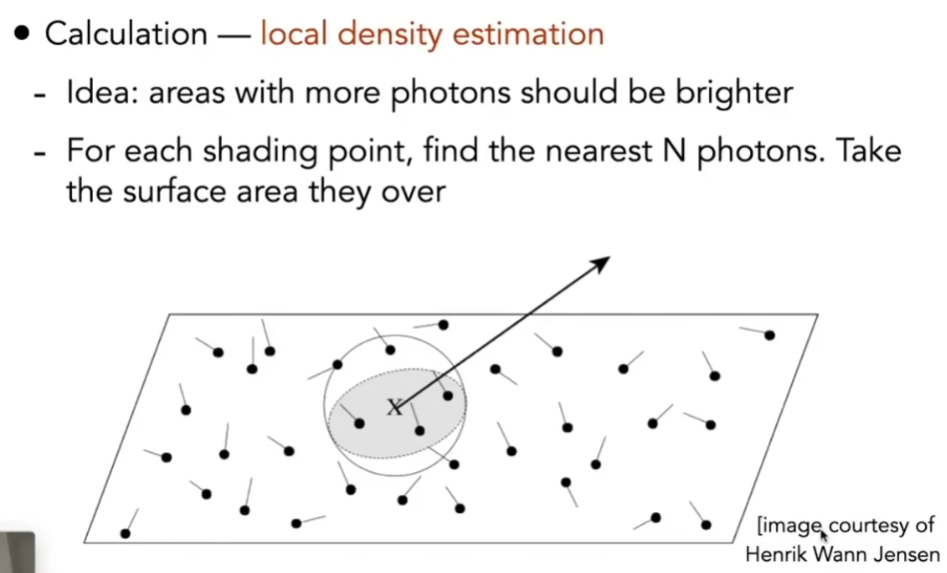
- 将两个步骤结合,计算局部的密度估计
- 光子越集中的部分越来
- 对任何一个着色点,取它周围最近的N个光子,找这N个光子所占的面积,接着算这些光子的密度

- 如果N取太小,噪声会很大;N取太大,画面会模糊
- 这就是为什么光子映射是有偏的方法
- 密度应该是当前一个点密度是多少,当前点周围取微小面积dA(dN / dA);而光子映射做的是给一定光子数,算它的面积(△N / △A)
- 对密度的估计是一个不正确的估计,而当有足够多的光子的情况下(极限情况),△A会接近dA
- 但只要不是无限个光子,这种方法一定会有点糊,所以叫做有偏的方法,但是一致的
- 在渲染中很好理解有偏和无偏
- 得到的结果有任何一点的模糊,就是有偏
- 一致的:虽然是有模糊的,但只要样本足够多,最后会让它收敛到不模糊的结果
Vertex Connection and Merging(VCM)
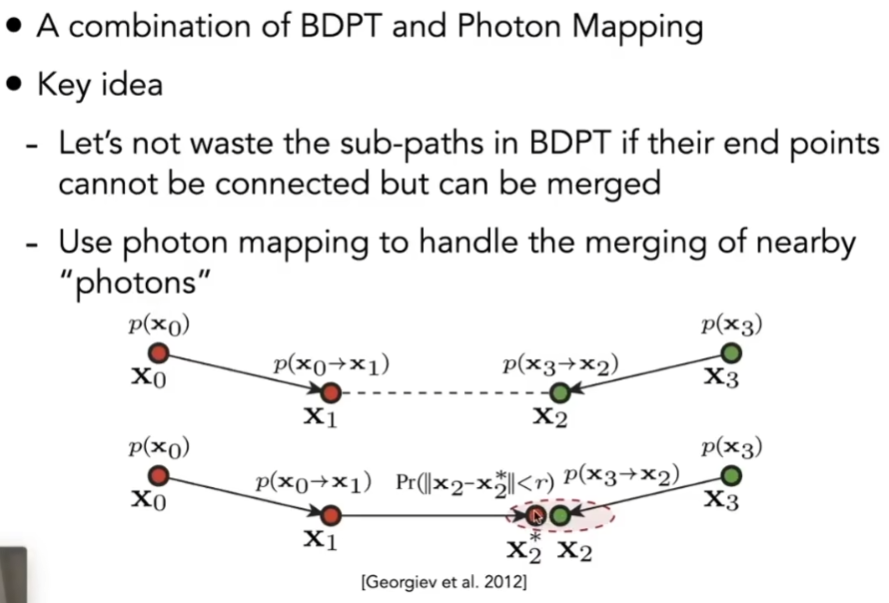
- 将双向路径追踪和光子映射结合起来
- 生成两个sub-path连起来,如果有的path满足两个端点非常接近,就不用连一条path,而是用光子映射结合起来
Instant Radiosity (IR 实时辐射度)
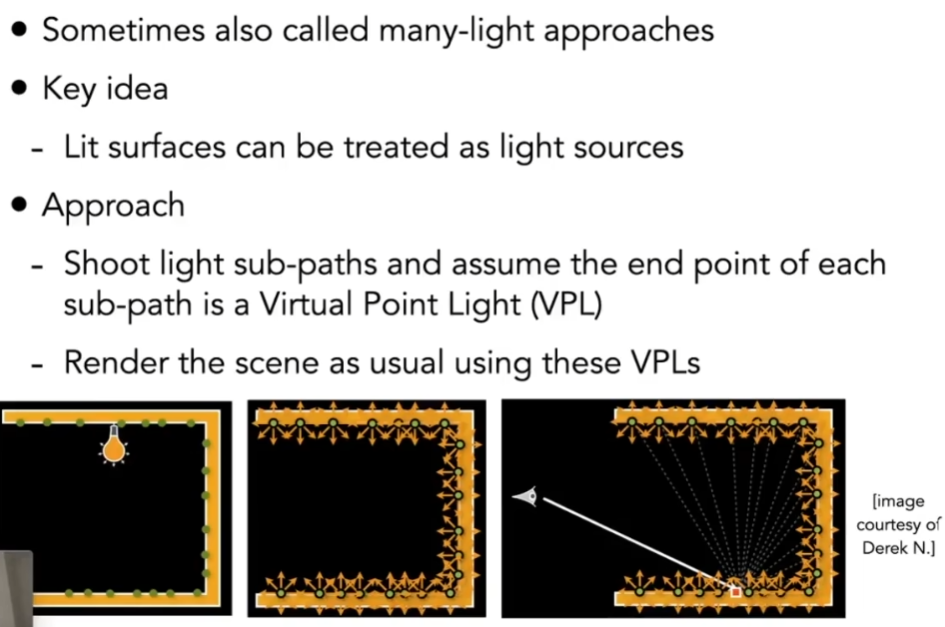
- 思想:已经被照亮的面都认为是光源,用它们再去照亮别人
- 从光源打出很多光线,停在某些地方,认为那些停住的地方形成了新的光源(VPL 虚拟光源)
- 当看到某一点时,用所有新的光源去照亮这一点,实际上是考虑光线弹射了两次

- 问题:在窄的接缝处会发光,因为之前把对立体角的采样改成了对面积的采样,面积 x cos / 两点间距离,两点间距离足够小时,得到结果非常大


外观建模

非表面模型
散射介质
如云、雾

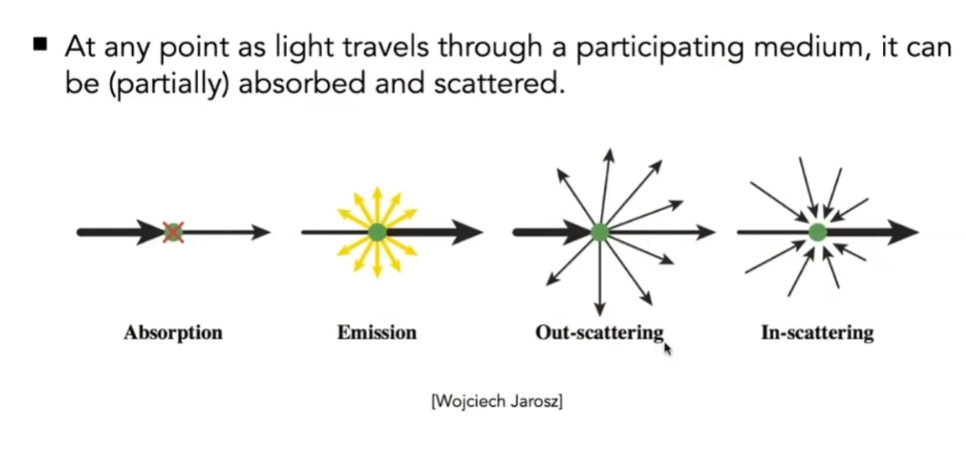
当光在行进过程中如果穿进了散射介质,会有若干事情方式
- 云中间有光源,先不考虑
- 云里面有小的冰晶,会把光线随机地打到不同方向去
- 光线传播过程中也可能接收到其他光线
- 在传播过程中逐渐消失,如乌云
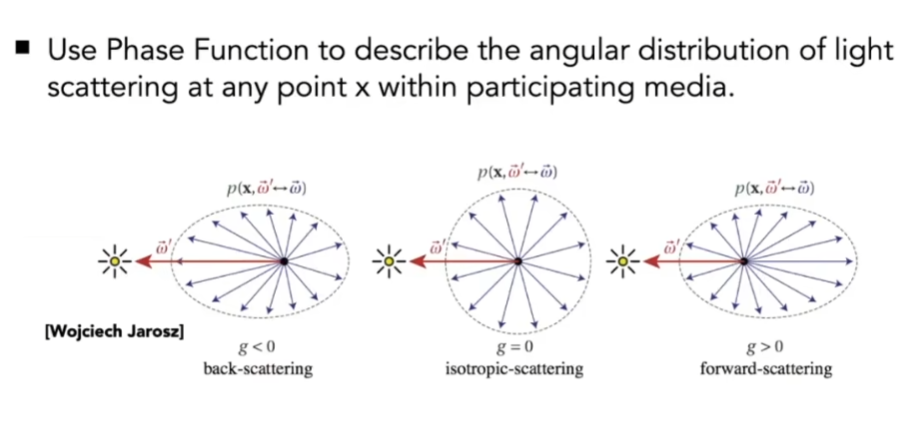
- 总之,光线在传播过程中,可能被吸收,可能被散射
- 而如何散射的,由相位函数(Phase Function)来定义
- 光线能传播多远,取决于介质(如乌云、薄雾)
- 光线停下后,考虑光线应该往哪个方向重新走,这就是散射
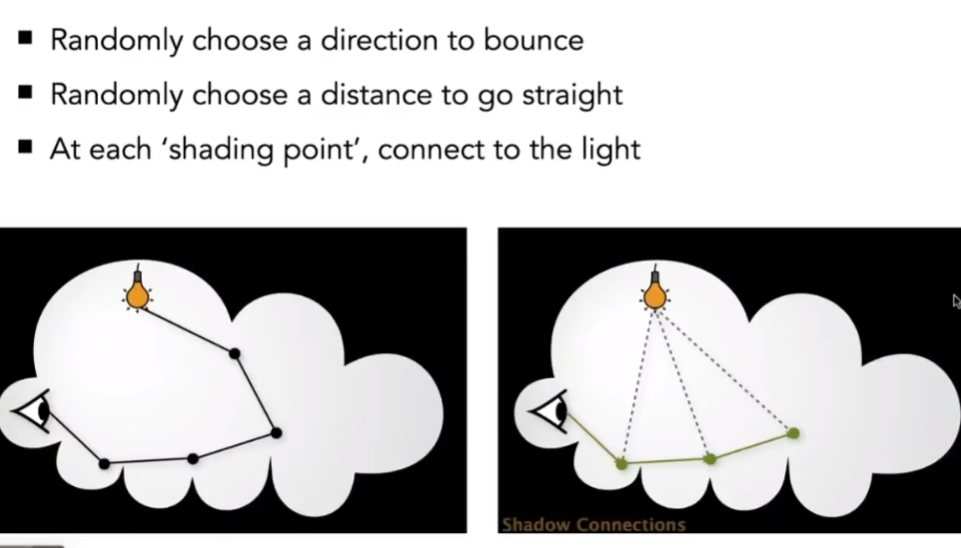
- 相当于光在物体表面做各种各样的弹射,只不过中间任何一个点都有可能发生方向的改变,最终都能找到一条连接光源的path,找到path后和各个弹射点相连,计算整个路径的贡献
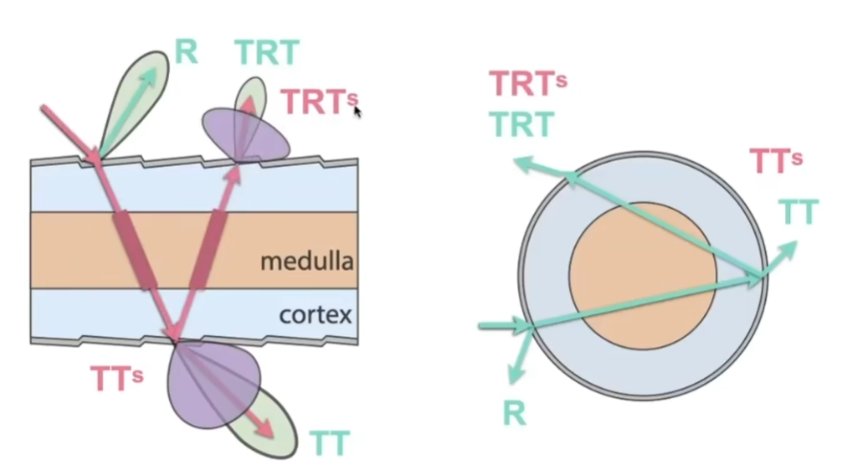
Hair Appearance

- 考虑光线和一根线的作用
- 有无色的高光和有色的高光,如何形成的呢
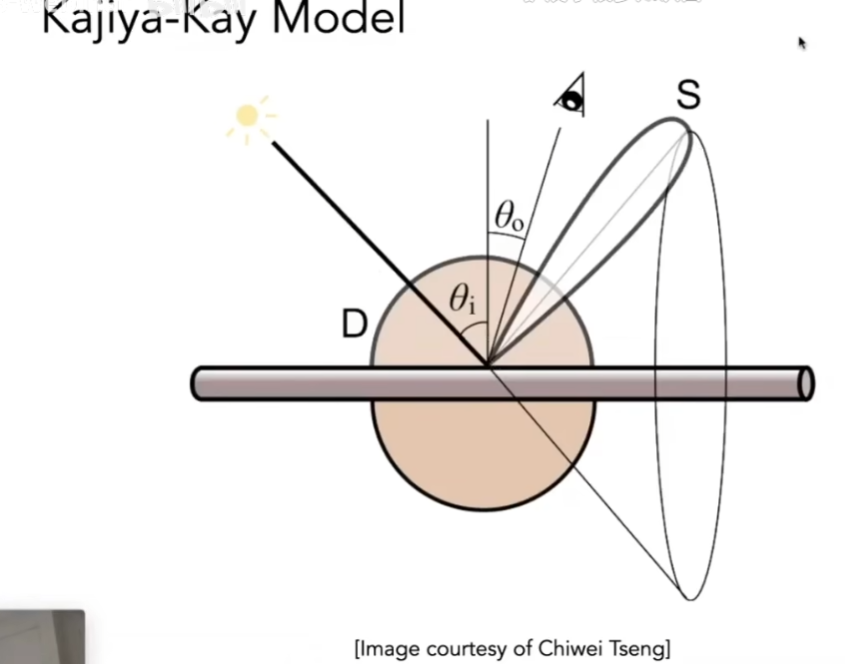
- 光线打到圆柱(头发)上,往四面八方散射,对头发来说,会散射出一个圆锥,同时一些光线会被散射到四面八方去

- 这种模型显然不好
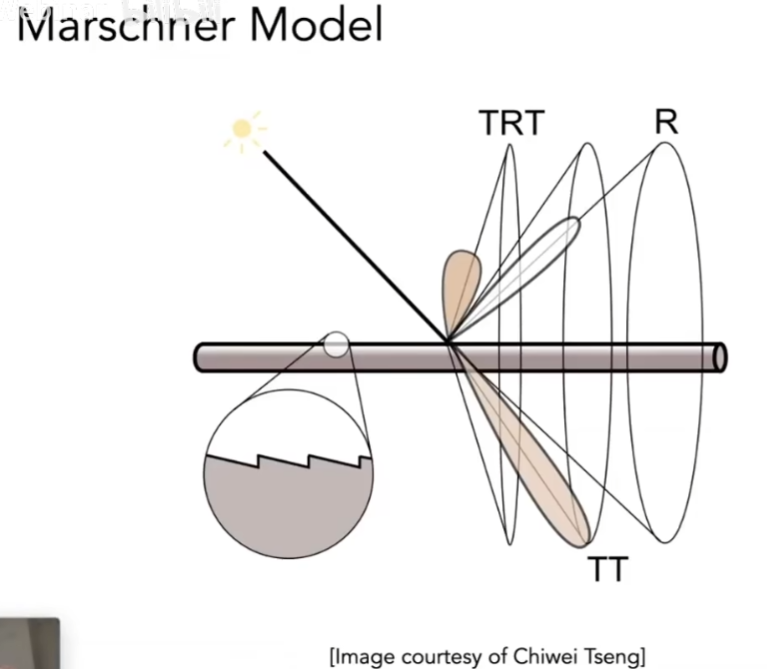
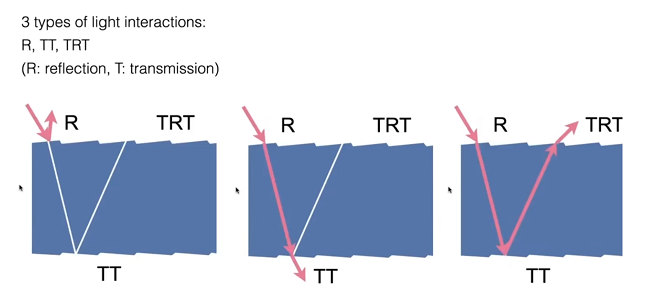
- 这种模型考虑光线打到圆柱的时候,肯定有一部分被直接反射掉(R);也有一部分会穿进去,发生折射(TT);还有一种是光线进入头发里面,在内壁上发生一次反射又往回走(TRT)
- 描述材质就是要描述如何跟光线作用
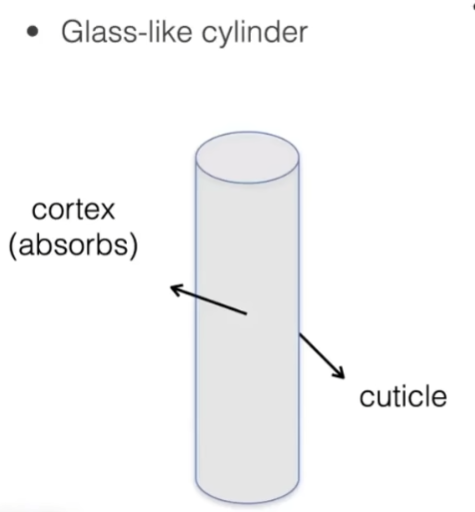
- 把头发当成玻璃的圆柱,局部是直的,它有两层结构,外层是cuticle(角质层),内层是cortex(皮质)
- 认为头发内部有色素,如果头发是黑的,色素多,吸收多
- 考虑三种光线和圆柱的作用:

- 综合考虑后,可以得到一个非常好的模型

- 而用人的头发模型不能用来描述动物的毛发
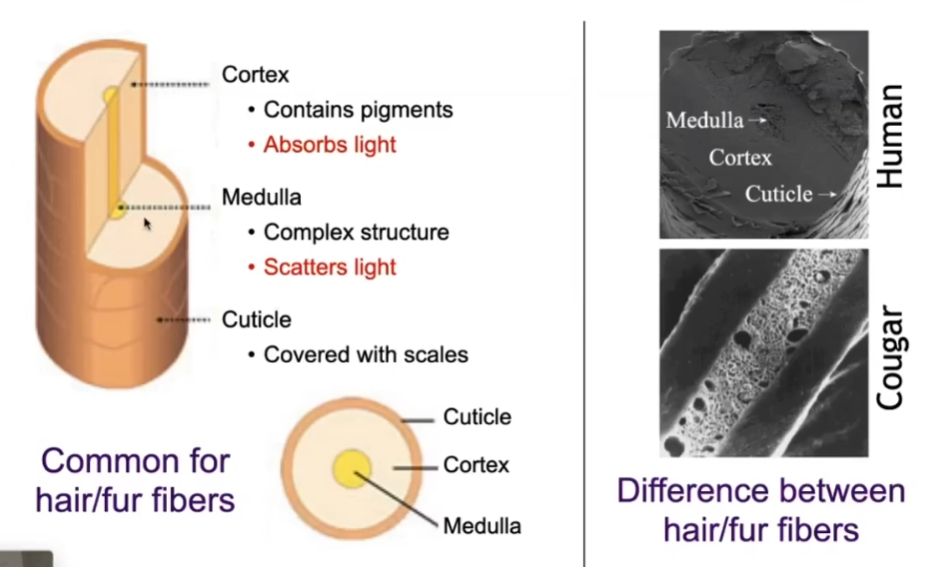
- 从生物结构来看,毛发有三层,而动物毛发的髓质比人的头发髓质要大很多,光线进去更容易发生散射
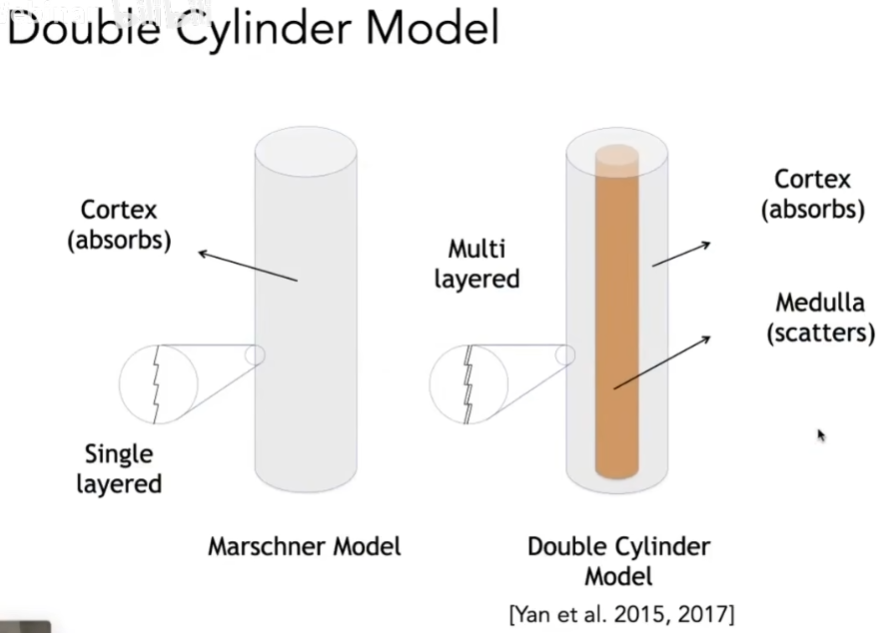
- 而事实上,髓质的影响确实很大,于是提出了双层圆柱模型

Granular Material

- 颗粒材质
- 一粒一粒的模型,一堆小东西形成的模型
Surface Models
- 半透明材质



- 为了描述光线的这种反射方式,定义为次表面反射(Subsurface Scattering)
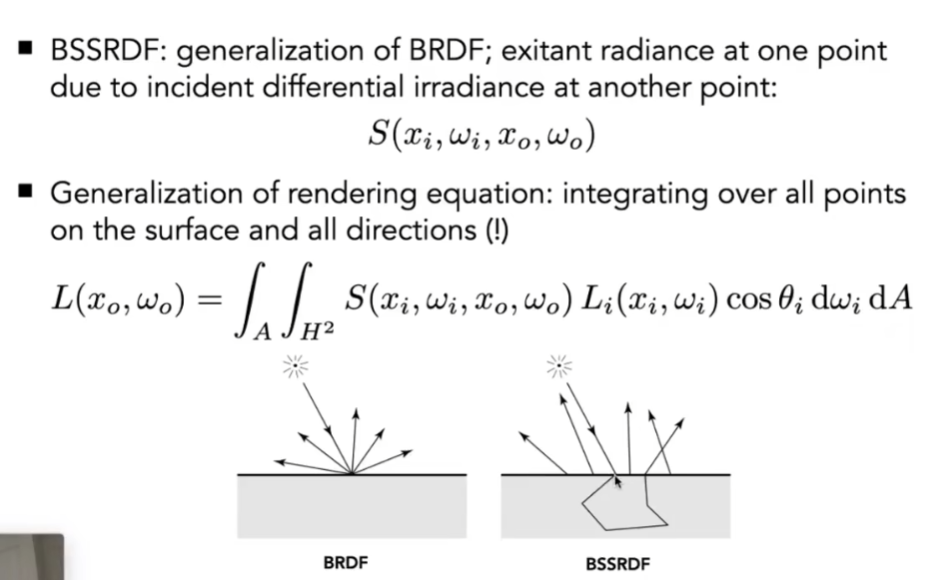
- 次表面反射可以理解为BRDF的延伸
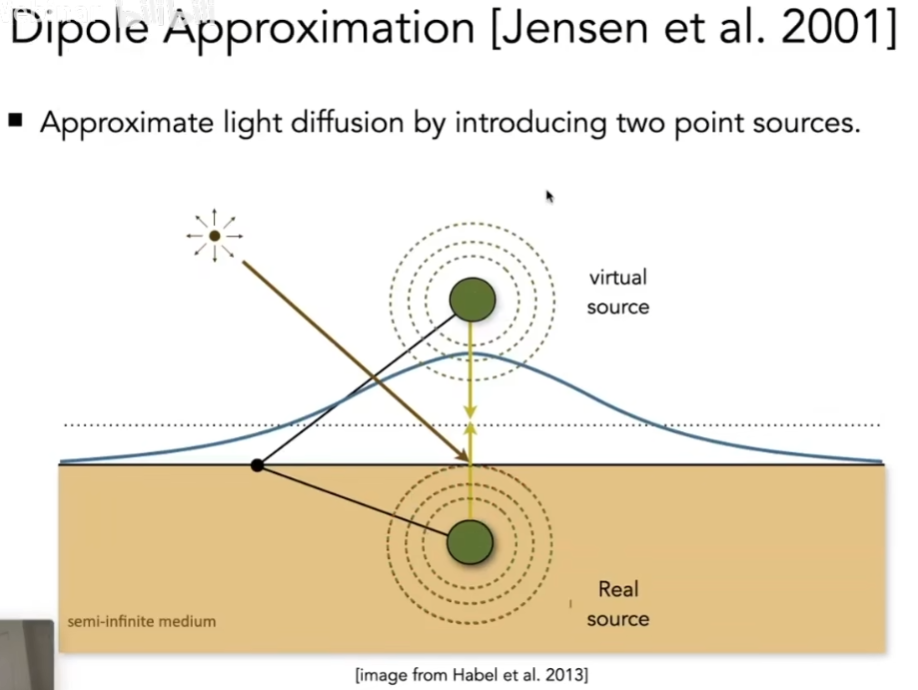
- 人们发现,半透明介质好像就是光打到物体上,这个物体底下出现一个光源,从底下照亮着色点周围的一片
- 为了真实,人们觉得一个光源不够,上方还得有一个光源,用这两个光源去照亮着色点周围的一块,很像次表面散射得出的结果,这个方法叫做Dipole Approximation



Cloth

- 布料是一系列缠绕的纤维构成的
- 它的缠绕有不同的层级
- 纤维(fiber)是最原始的概念,一根一根的,如一根羊毛就是一根纤维
- 纤维经过第一次缠绕可以缠绕成不同的股(Ply)
- 不同的股再经过缠绕会形成线(Yarn)
- 再被织成布(包含机器织的布和手工织的毛衣等)
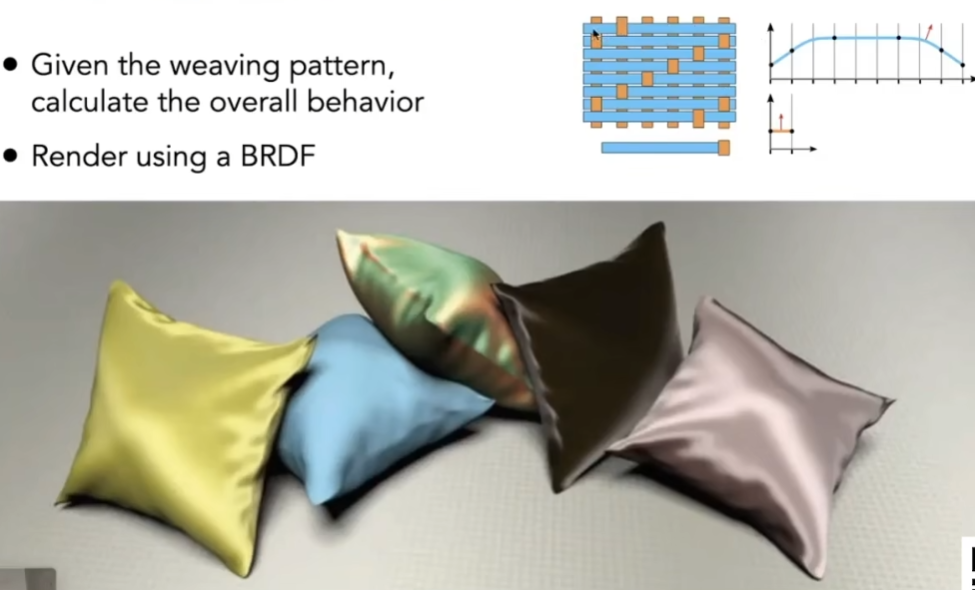
- 这种材质的渲染肯定和织的形状有关系
- 有的布本身真的在一个平面上,可以用BRDF,而像天鹅绒这种不是一个平面,就不能用BRDF来描述

- 一个办法是认为是空间中分布的体积,划分成一个个非常细小的格子,每个格子里面知道纤维的朝向分布、复杂程度等,就可以把这些性质转换成光线的吸收、散射,好像是在渲染云一样
- 能得到相对准确的结果,但计算量大

- 把每一根纤维都渲染出来
- 同样是计算量大
Detailed Appearance


- 渲染出的结果往往非常完美
- 而真实世界中的物体会存在各种细节,比如划痕
- 微表面模型提到,最重要的是微表面的法线分布
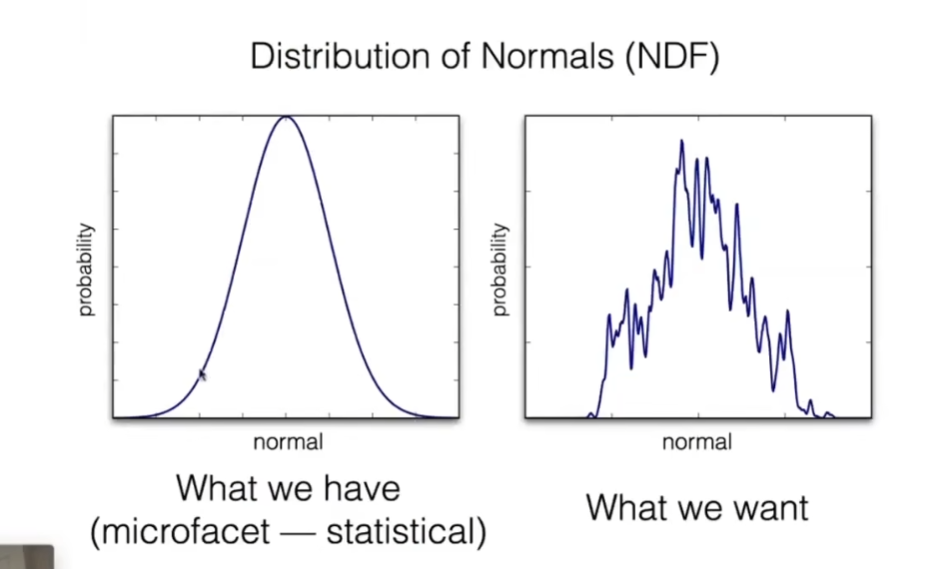
- 大家描述这种分布,一般用的都是简单的模型,比如正态分布、高斯,用这种方式去描述,得到的自然是看上去没什么细节的结果,因为法线分布并没有体现各种各样的变化和细节
- 实际上我们要的是基本符合统计规律,又有自己带的细节的模型

- 细节的渲染十分困难
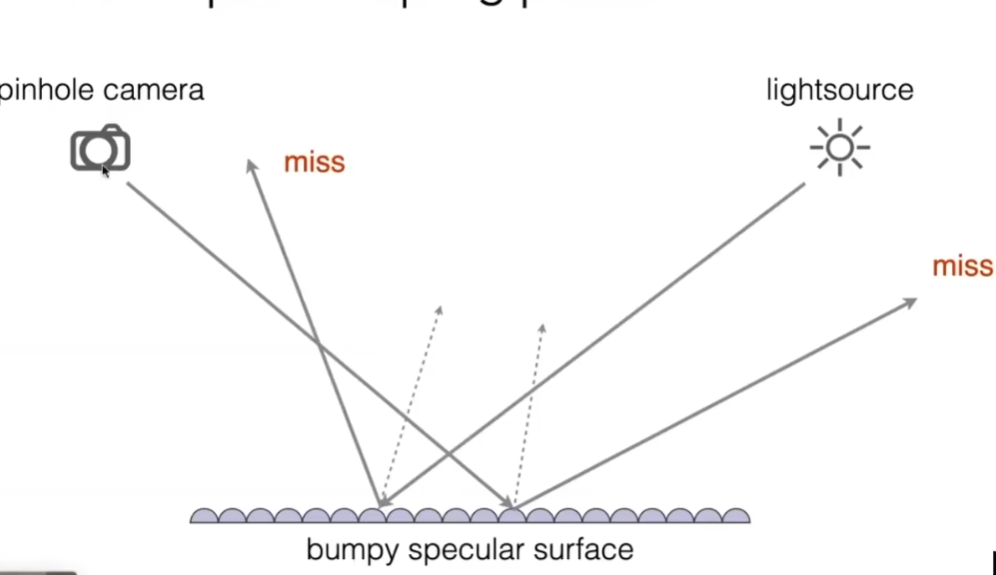
- 问题就在于我们认为每个微表面是一个镜面,摄像机打出的光线很难打到光源,反之亦然
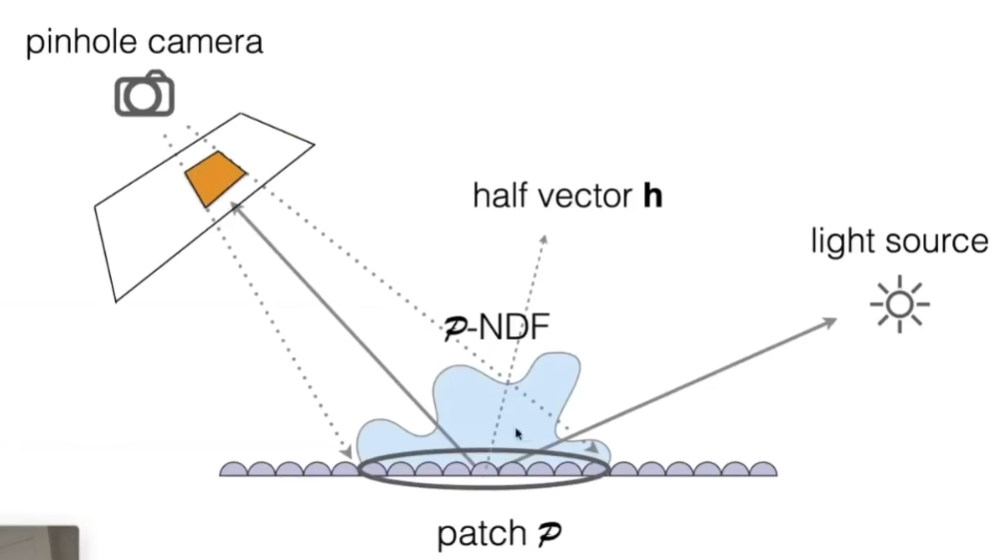
- 解决办法是考虑一个像素会覆盖很多的微表面,而如果能把这块微表面的分布算出来,替代原来光滑的分布,并且用在微表面模型里
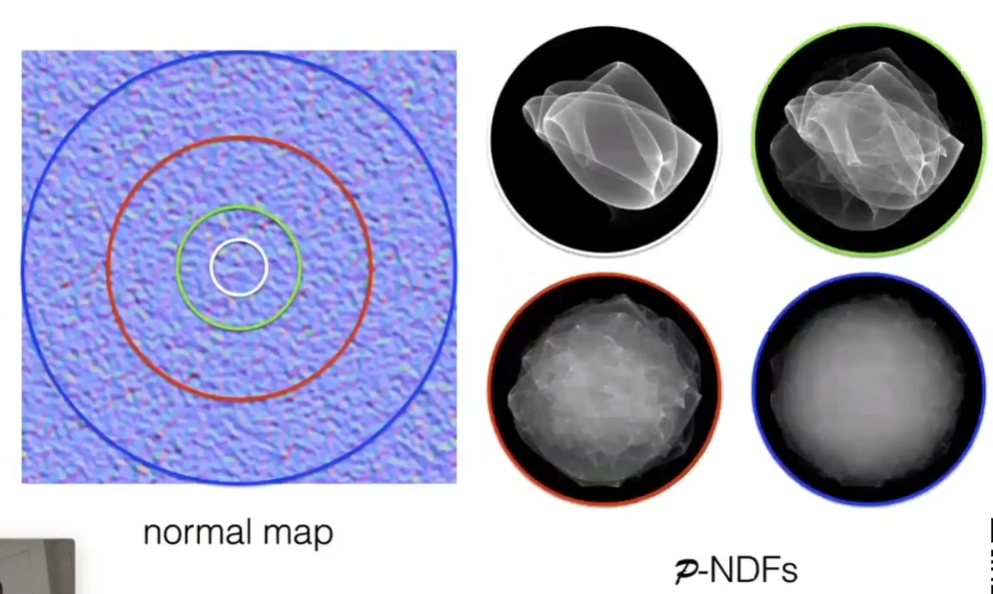
- 如果考虑一个像素覆盖了多大的范围,会得到各种各样的法线分布NDF
- 如果一个像素覆盖了很多的微表面,这些微表面的法线分布自然而然的显示出圆形的统计学规律
- 如果覆盖的范围小,就会显示出很独特的性质

- 而且不同类型的法线贴图会引起不同的分布



- 在物理上,当物体非常小的时候,小到和波长相当的时候,就不能假设光是沿直线传播了,必须假设这个光是一个波


- 在一个小黑屋里,用一个点光源照亮金属,可以发现不是一个颜色
- 用白光来照射物体,就应该反射出白的,如果不是白的,就一定有波动光学发生
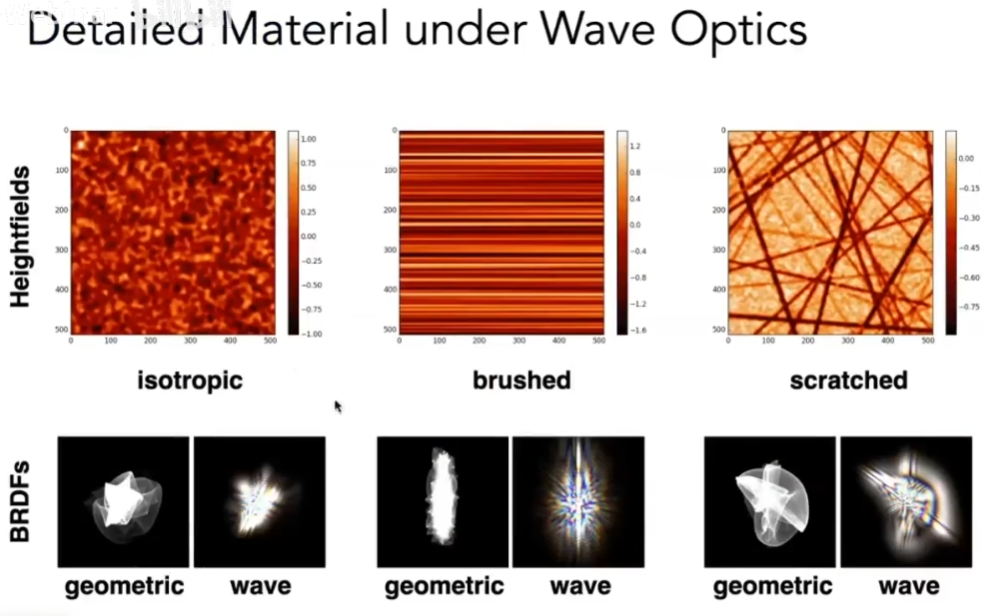
- 波动光学得出的BRDF跟几何光学得出的BRDF挺像的,但是又有不连续的特点,这是因为光的干涉,使得某些地方强某些地方弱
Procedural Appearance
- 程序化生成的材质
- 用一定的方式去指导材质的生成,不需要真正的生成它,而是动态地查询它

- 如果定义一张三维的纹理,存储量太大
- 不存纹理,定义一个空间中的函数f(x,y,z),什么时候需要用,就去查,这种函数就叫做噪声函数
Lecture 19 Cameras, Lenses and Light Fields
注:以下所描述的”棱镜”都为Lenses,应该被称做”透镜”
Imaging = Synthesis(合成:光栅化成像、光线追踪成像) + Capture(捕捉:如相机拍照)
Camera

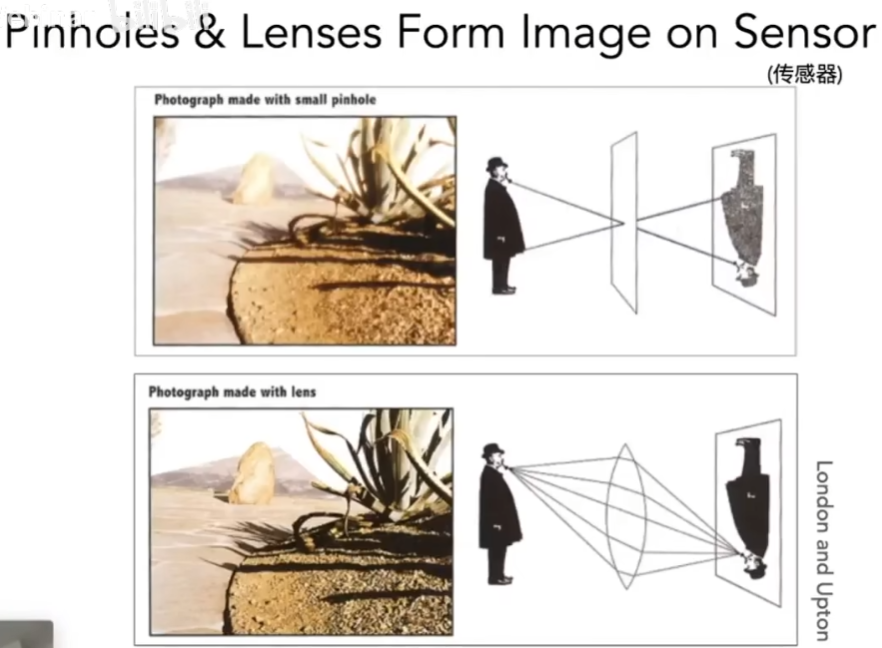

- 控制光在1/n内进入相机

- 记录光的Irradiance

Field of View (FOV 视场)
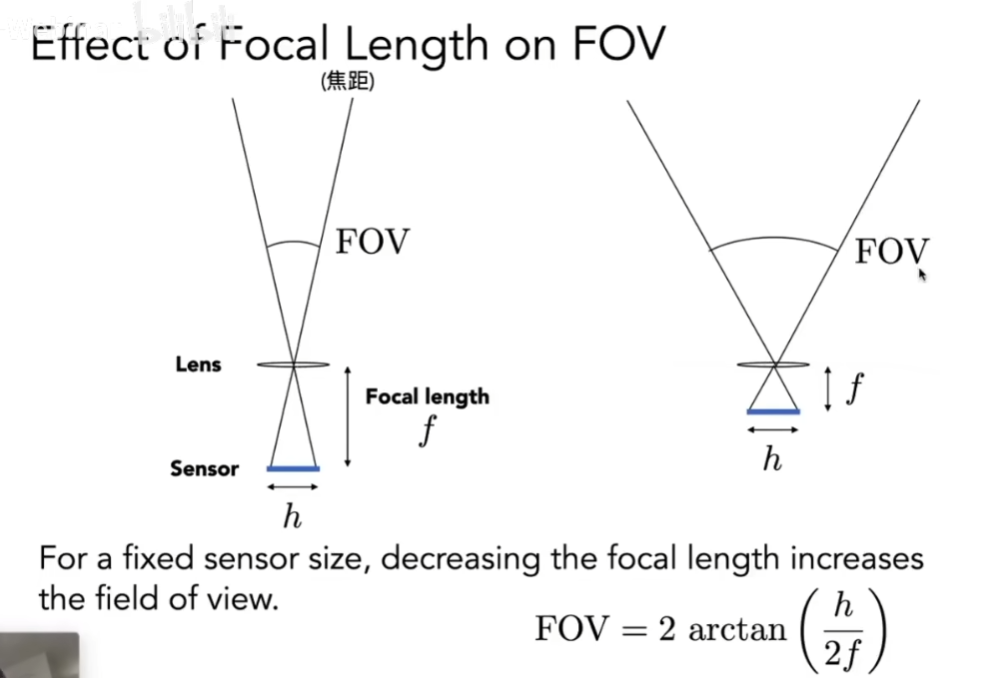
- 即能看到多大的范围

- 人们通常定义FOV的时候,认为是以35mm格式的胶片为基础,通过定义焦距的方式来定义FOV
- FOV越窄,可以看到的东西越远

- 如果能改变传感器的大小,小的传感器就对应小一点的视场

- 缩短焦距让小的手机也能达到相同的FOV
- 平常一般会固定传感器的大小,只用焦距来衡量
- 对于渲染器来说,传感器(Sensor)负责记录最后每个像素收到的Irradiance有多大,胶片(film)决定最后成什么样的图片格式
- 对于目前来说,可以把这两个概念混淆着使用
Exposure
- 曝光


- 相机能够影响照片亮度的因素
- f-stop(f数):调节光圈的大小,仿照人的瞳孔,在暗的环境下瞳孔会放大,单位时间可以接收更多的光,反之相反
- 快门速度:快门开放的时间越短,意味着更少的光会进来
- ISO gain:可以理解成后期处理,简单理解为最后接收到多少能量,乘以一个数
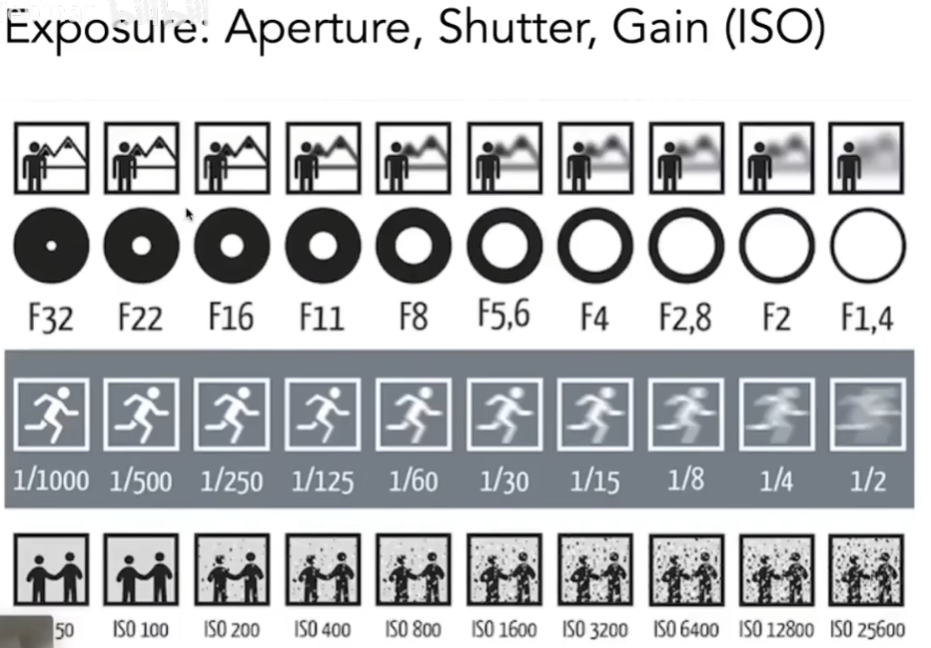
- f数越小,光圈越大
- 1/1000指开放1/1000秒,ISO的增长可以认为是简单的线性增长
- ISO能提高亮度,同时也会提高噪声

- 快门时间越久,让光进来的时间越久,在这段时间里如果物体在做运动,则运动的距离越长,得到的运动模糊越严重
- 反之,快门时间不变,物体运动的越快,运动模糊越严重

- 为了减少运动模糊,要求拍照不要手抖
- 或减少曝光时间,而减少曝光时间必然会减少收到的光线使得画面变暗,此时需要调节ISO,上表为一系列相同曝光度的对应参数
- 而大光圈会引起前景深的问题,快门时间会影响运动模糊,这两种情况是需要权衡的

- 运动模糊不一定是坏的,如体现赛车的速度

- 由于快门的打开需要一个过程,在这个过程中拍摄的高速物体,会产生Rolling shutter问题,产生不同位置的图像有可能记录的是不同的时间的结果,造成扭曲的现象

- 高速摄影
- 人们不希望有严重的噪声,因此使用大光圈,而不直接提高ISO

- 延时摄影
- 用小光圈慢慢拍
Thin Lens Approximation


- 真正的棱镜非常复杂
- 有些棱镜并不是把光聚到一个点上
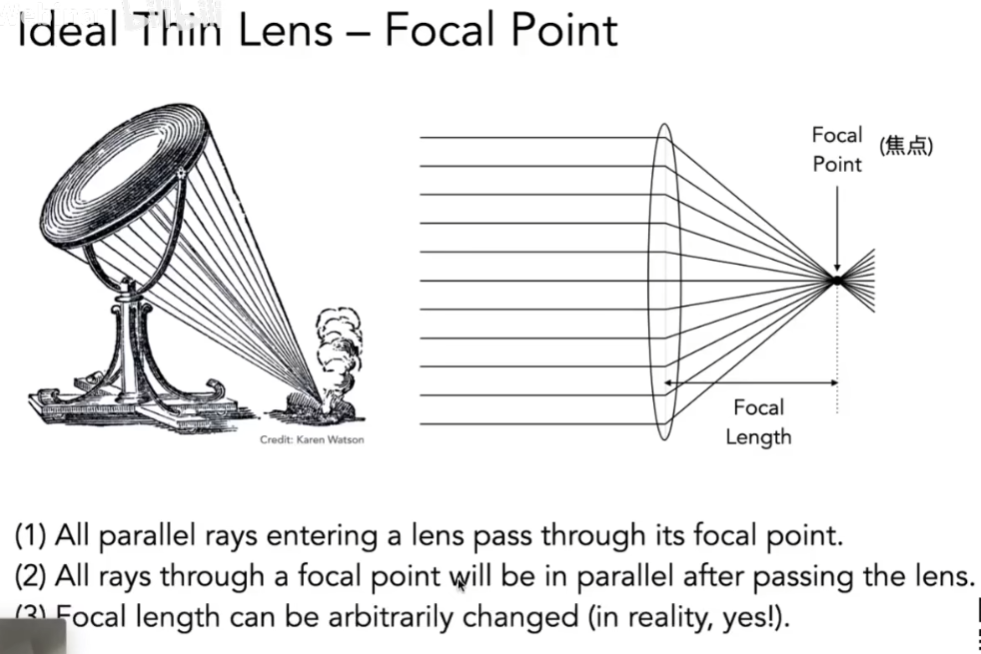
- 我们研究的是一种理想化的薄的棱镜,棱镜本身厚度忽略不计
- 平行光打进来,都会经过一个点,叫做焦点,焦点到棱镜中心的距离叫做焦距
- 光路有可逆性,如果光线穿过焦点,被棱镜折射后会变成平行的一束光
- 假设这个薄的棱镜,可以任意改变它的焦距。而实际上棱镜生产出来后,是不能改的,这正是相机中使用棱镜组的好处,使用棱镜组就类似一个可以调焦距的棱镜
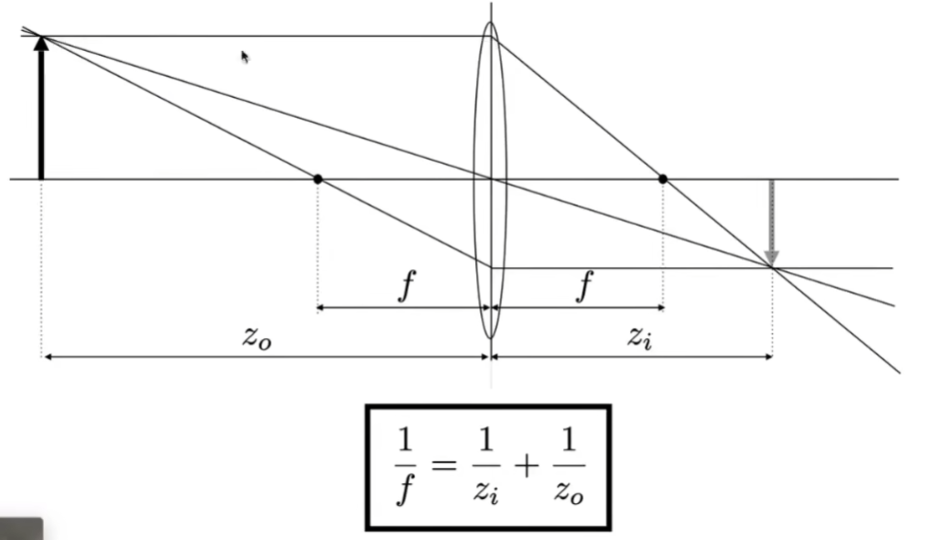
- 棱镜会满足基本的物理规律,定义物距、相距和焦距
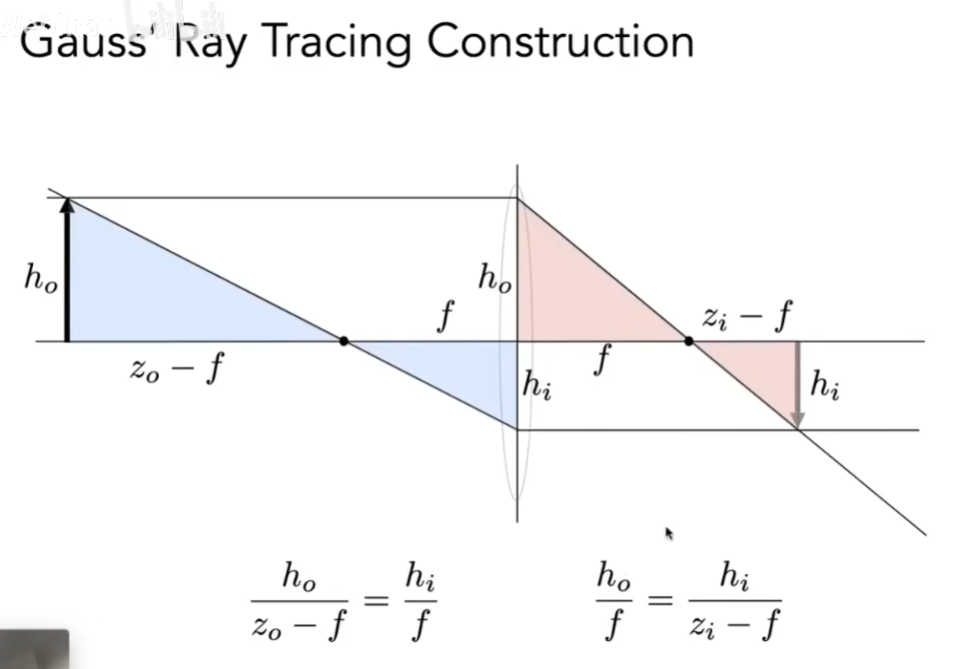
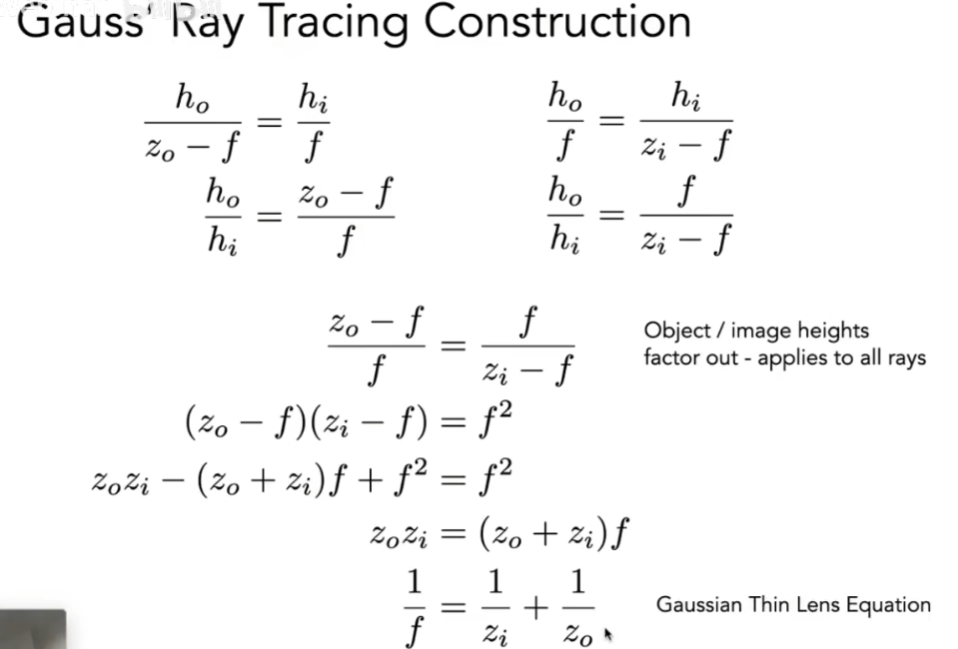
用相似三角形来推导
反应了相距、物距、焦距三者的关系
通过薄棱镜,可以解释好多问题
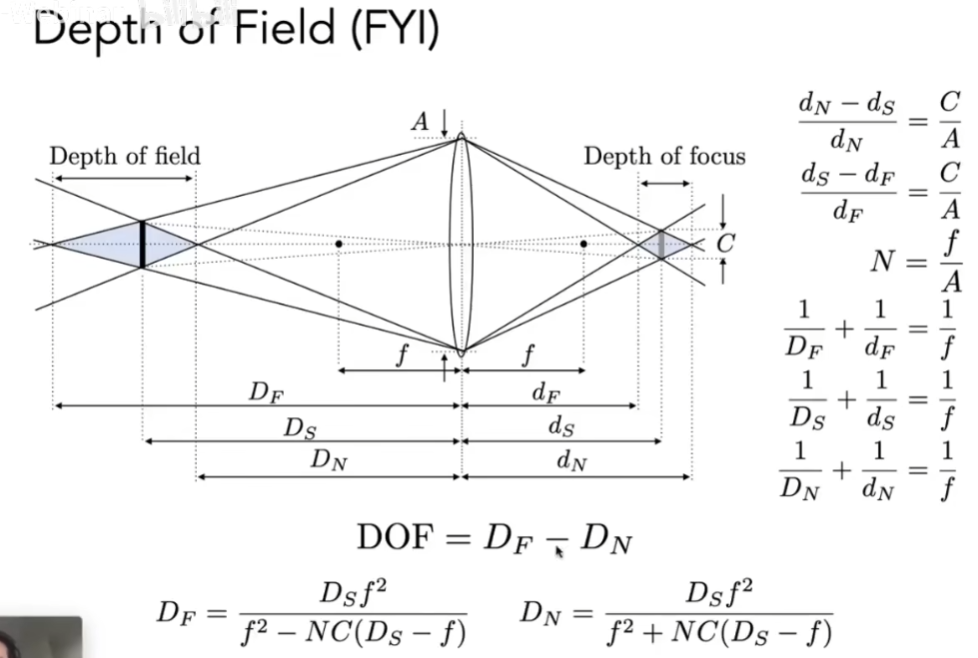
1.景深
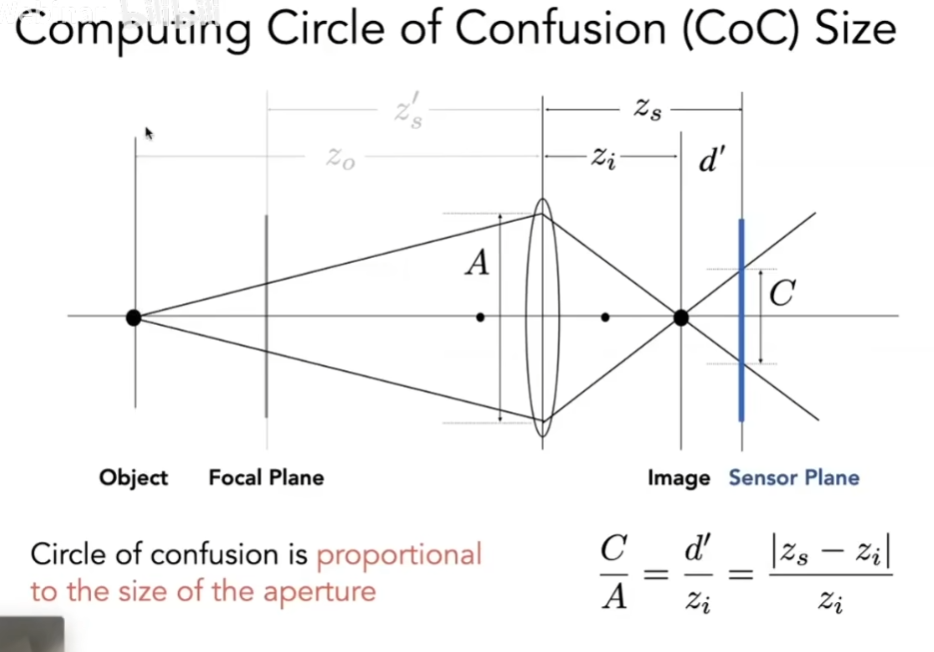
CoC:一个点成像过来,反应到Sensor上变成了一个圈
CoC跟光圈大小成正比


- N(f数) = f(焦距) / A(光圈直径)
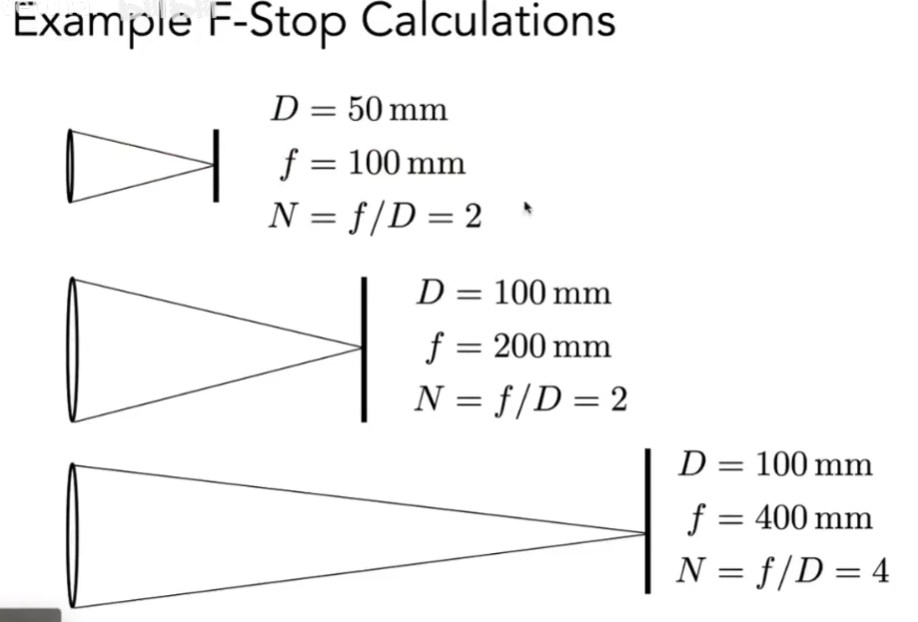

- CoC和N有反比关系
- 所以拍清楚的照片通常用小光圈
Ray Tracing Ideal Thin Lenses

- 模拟薄棱镜做光线追踪
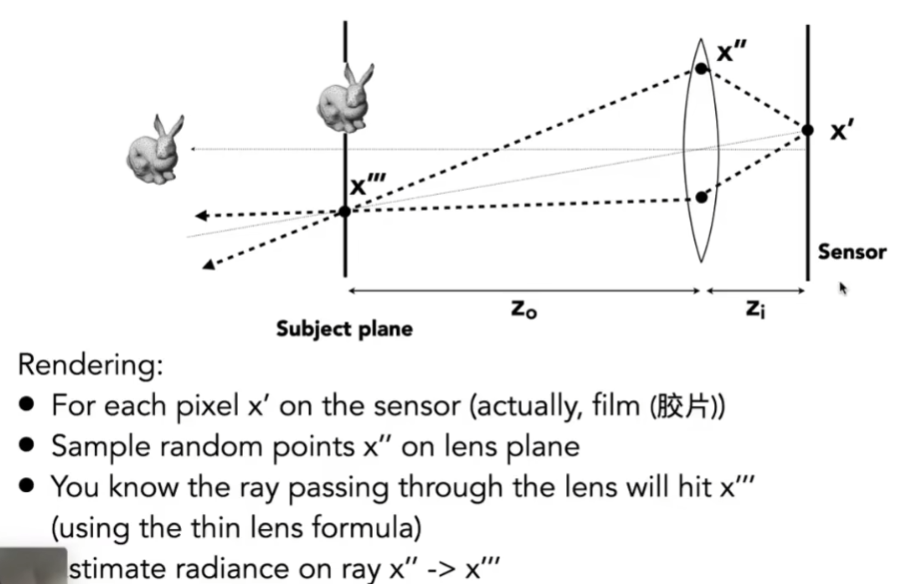
- 一种设定方案:
- 确定成像平面大小,定义棱镜属性(焦距和光圈大小)
- 定义这个棱镜离场景中某个平面有多远(物距zo)
- 计算相距
- 渲染:
- 在成像平面上选一点x’
- 在透镜上选一点x’’
- 将这两点连一条线
- 可以得到x’’’
Depth of Field

- 大光圈得到大的CoC,一个点会得到大的圆,但总归有部分是不模糊的(Focal Plane)
- 用大小光圈会影响模糊的范围
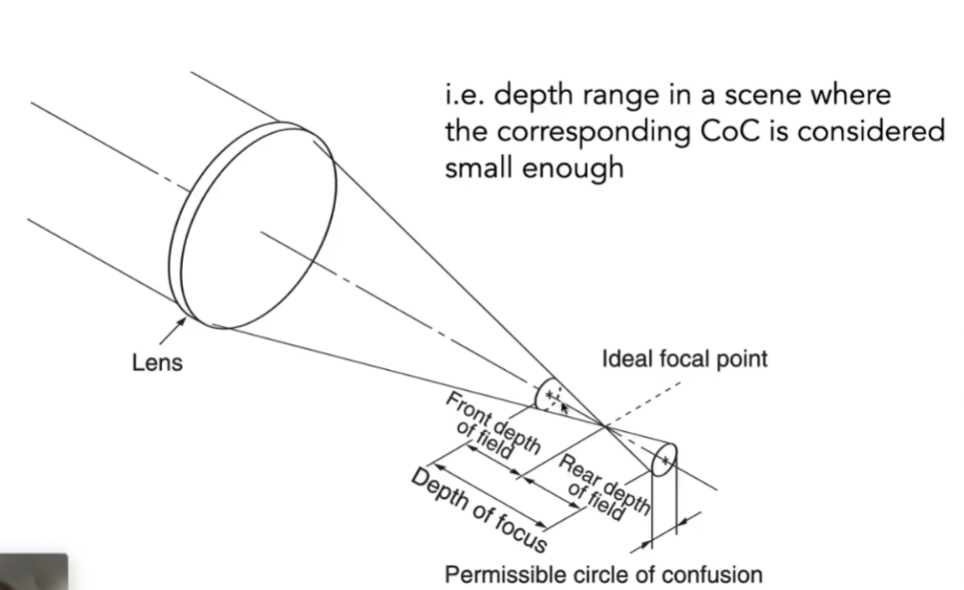
- 景深就是指在场景中有一段深度,这段深度经过透镜后会在成像平面的附近形成一段区域,这段区域内认为CoC都是足够小的
- 景深就是指成像清晰的一段范围
Lecture 20 Color and Perception
Light Field / Lumigraph (光场)
- 人们看到的是从各个方向进来的光线,而看不见光线从多远进来,从什么地方进来
- 可以用全光函数(The Plenoptic Function)来描述人可以看到什么东西

- 假设人站在场景里位置固定,往四面八方去看,可以用极坐标表示任何一个方向

- 改进函数,引入波长(表示不同颜色)
- 再扩展一个时间t

- 再考虑空间中任何一个位置
- 最后把这个函数理解为:在任何一个位置、往任何一个方向看,并且在任何时间,看到不同的颜色
- 就拿这个七维的函数当做全光函数
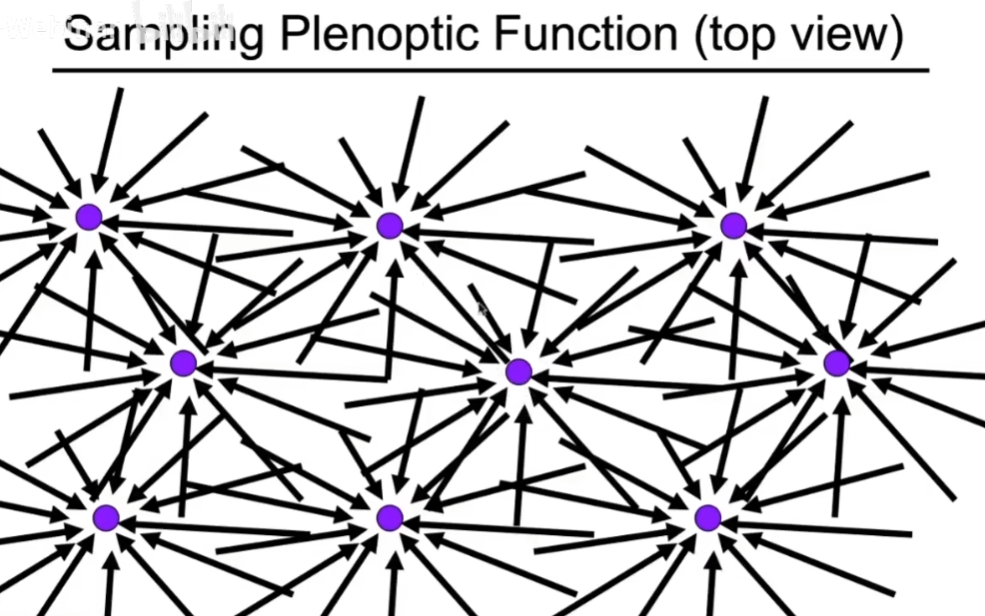
- 紫色点并不是离散的,可以放在任意位置,能从任意方向知道过来的光是多少,方向也应该是连续的
- 光场是全光函数的一小部分
光线
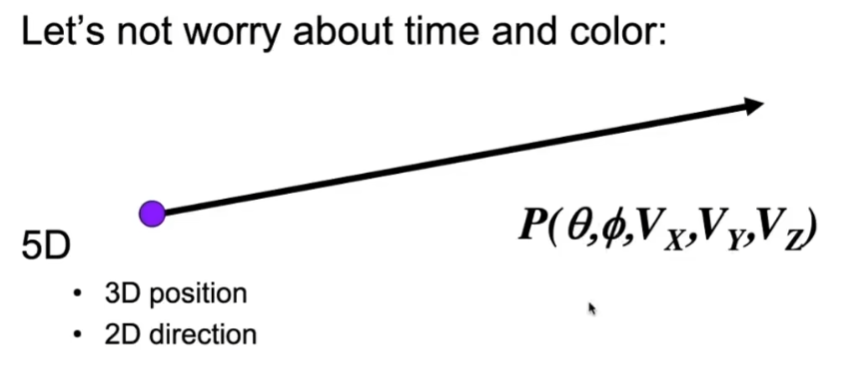
- 起点是(VX, VY, VZ),方向是θ
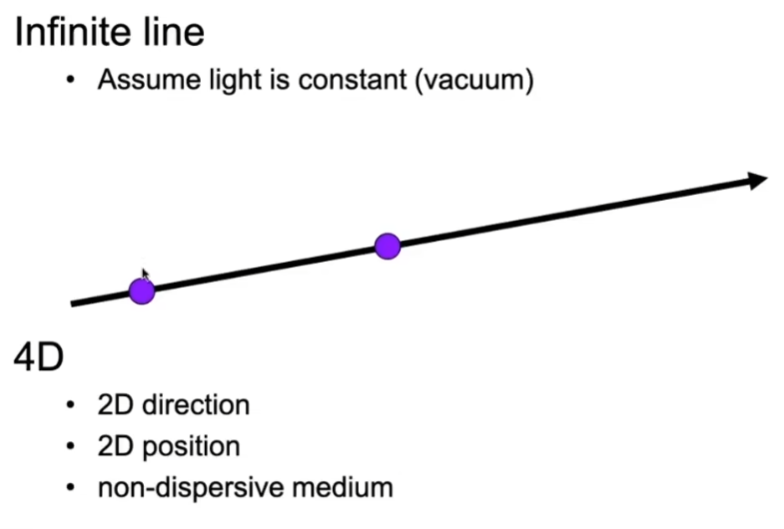
- 可以用不同的方式定义光线
- 比如取任意两点,假如方向已知
表面
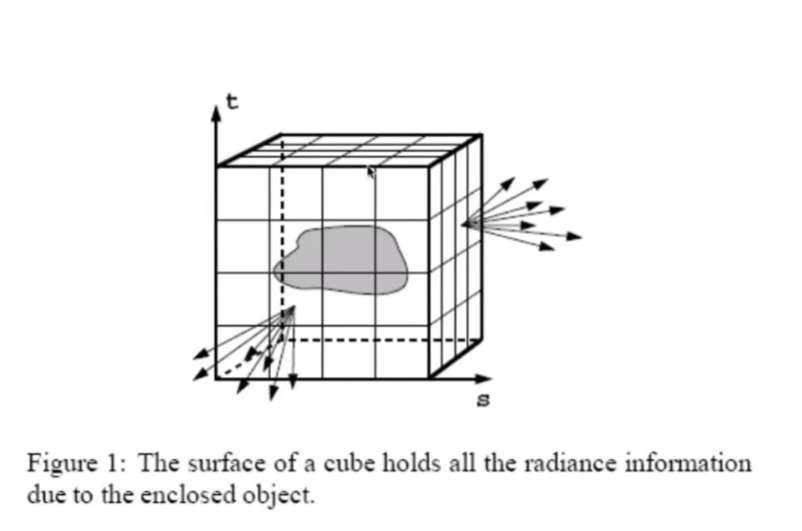
- 对于定义任何一个物体的表面
- 可以把任何一个物体放在一个包围盒里
- 看向物体,无非是从任何位置、任何方向
- 根据光路的可逆性反过来理解,要想描述这个物体能被看到的所有情况,就要描述这个物体在它的包围盒上,它在任何一个位置往任何一个方向过去的光线,就可以得到从任何一个位置看向这个物体是长什么样的
光场
- 相当于是包围盒上有一个点,观察位置一个点,两点确定一条光线。知道包围盒上的位置,知道方向,就可以去查询记录的函数
- 这个函数记录了不同的点(物体表面不同的位置),往各个不同的方向的发光情况,把这个情况记录下来,就是光场
- 总结:光场就是在任何一个位置,往任何一个方向去的光的强度
- 光场是全光函数的一小部分,只是二维的位置和二维的方向
- 位置:三维物体的表面其实在一个二维空间中,可以理解为纹理映射,用u、v就能表示任何一个位置
- 方向:任何一个空间中的位置,都可以用θ、Φ表示
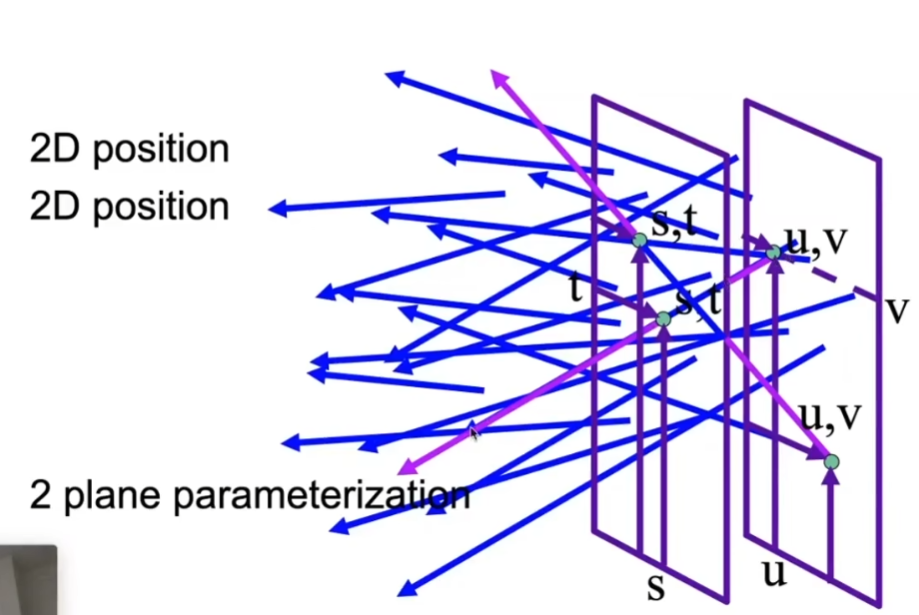
- 光场的一种参数化方式:取两个平行的面(uv、st),各取一个点连线,考虑所有的可能性
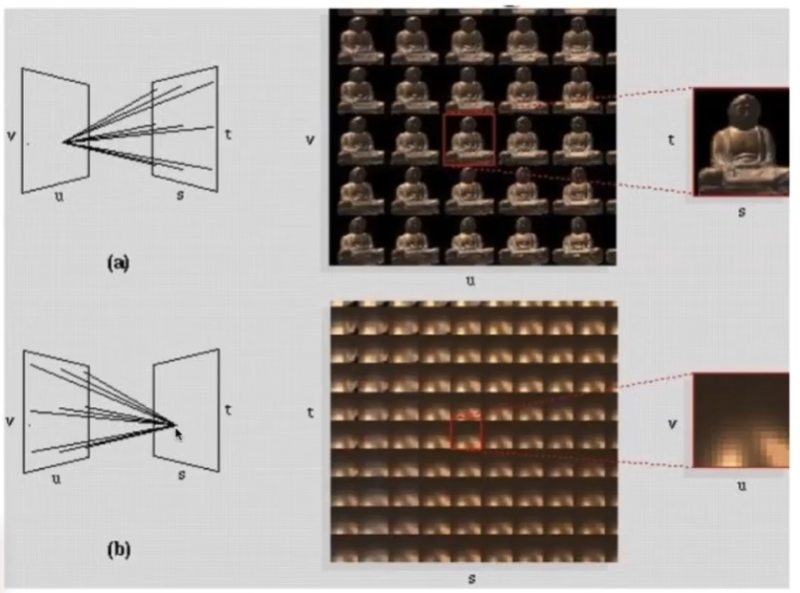
- 从某个角度看向整个世界,拍一张图,把所有这些图组织在一块,这就是整个光场
- 光场的另一种理解方式
- 把原本记录在一个像素上的光分别记录在不同位置

- 光场摄像机:支持后期的重新聚焦
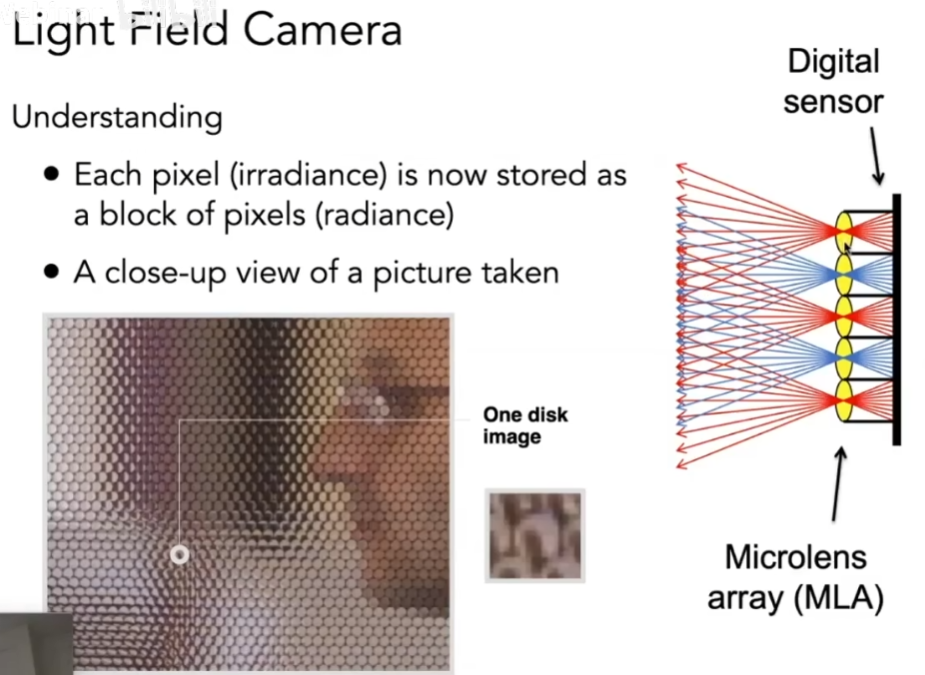
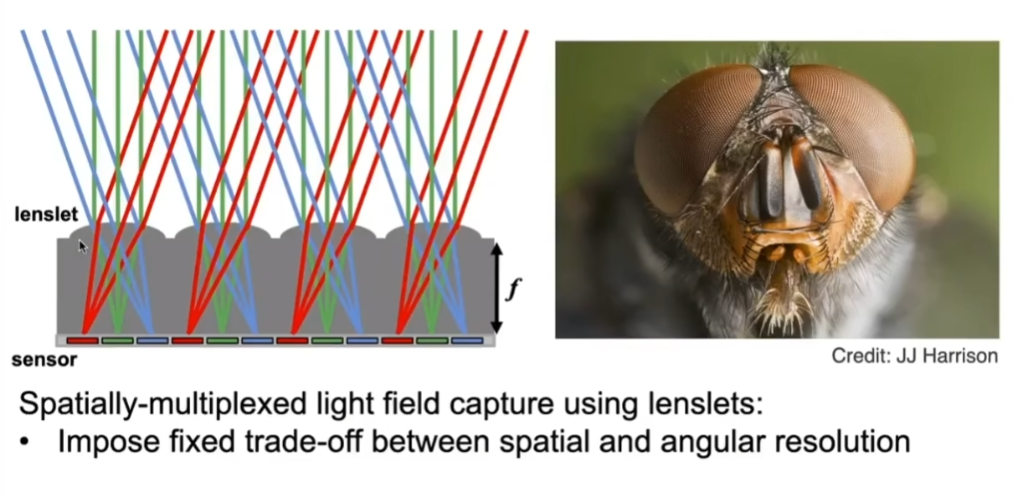
- 原理就是把原本的像素换成微透镜,这些微透镜会把来自各个方向的光给分散到不同的方向上去,将感光元件往后挪一点点
- 原本记录一个像素,现在记录一块像素
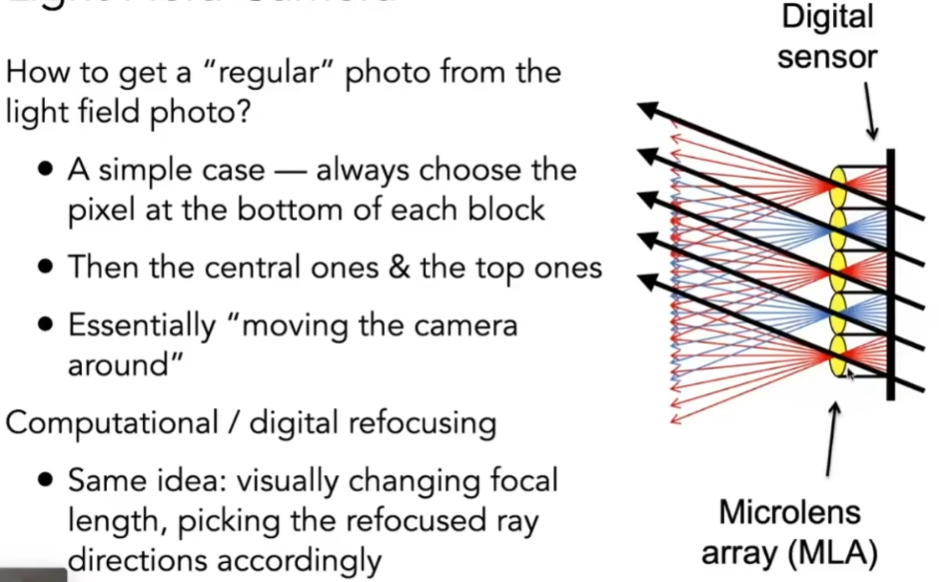
- 为了得到最后的图片,每个像素都选取同一方向的一条光线,记录在一个像素的结果上
- 相当于有了这个光场以后,我们可以虚拟地移动摄像机的位置

- 光场相机的问题:
- 分辨率不足:原本一个像素记录一个像素的信息,现在用一百个像素记录一个像素的信息。胶片的分辨率变成空间上的分辨率乘以方向上的分辨率
- 高成本:高精度胶片、透镜
Physical Basis of Color
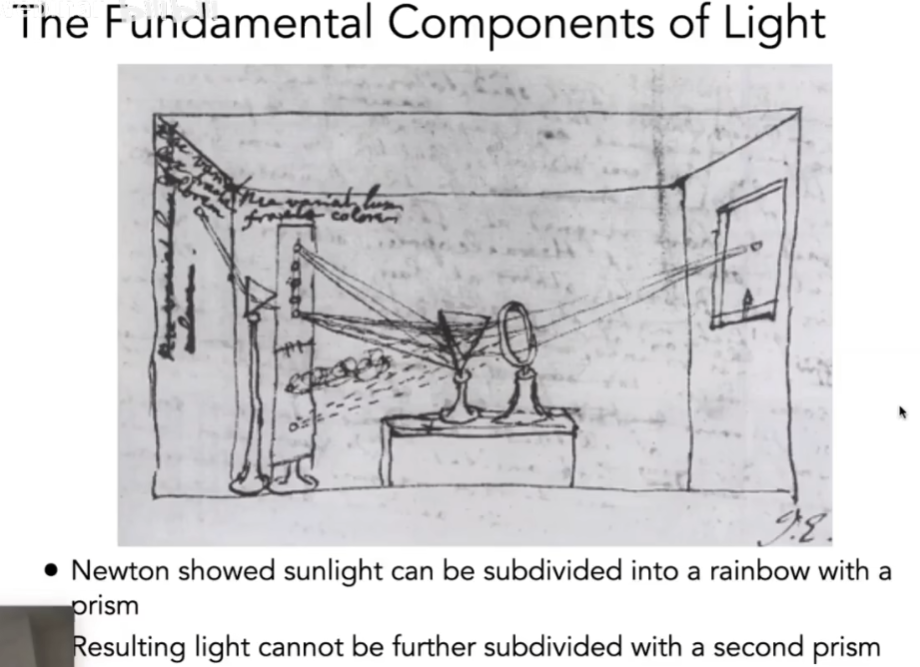
- 牛顿通过实验发现,颜色其实是很多基本颜色混合出来的结果
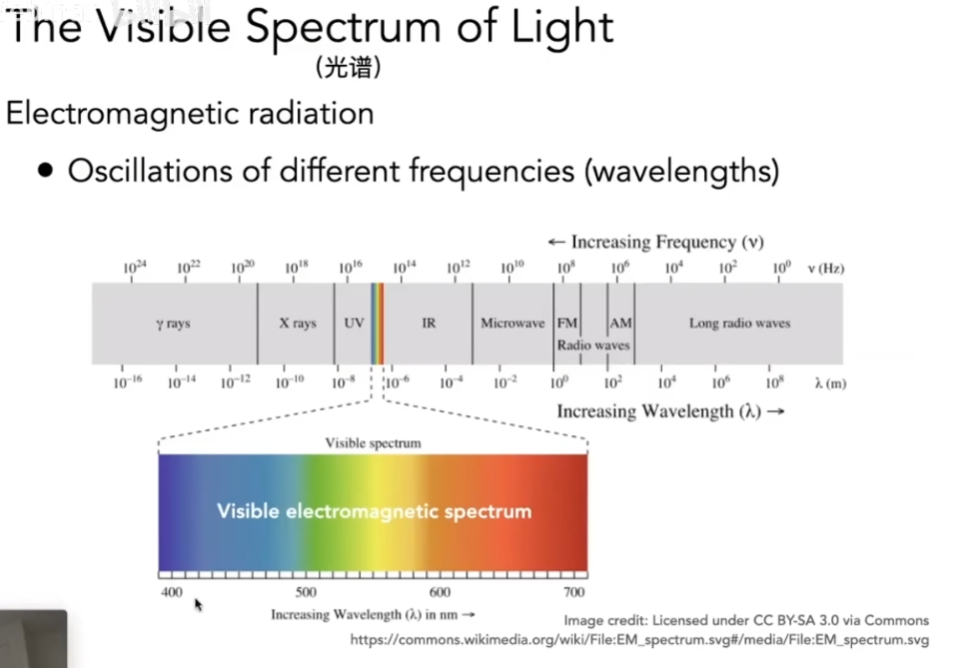
- 不同的波长对应不同的折射率,而任何一种光一定对应某一种光谱
- 光谱就是光线的能量在不同的波长上的分布
- 光谱是一个很长的范围,而图形学中关心的是可见光的光谱,分布在大概波长400nm ~ 700nm之间

- 谱功率密度(SPD):光线在不同的波长的强度是多少
- 通过SPD,可以描述光在各个波长上的分布
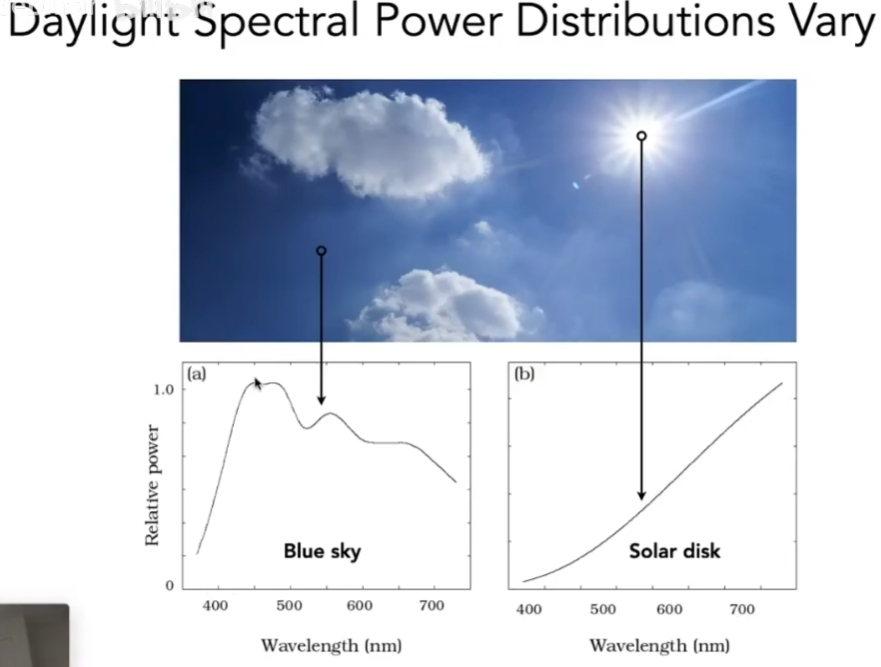
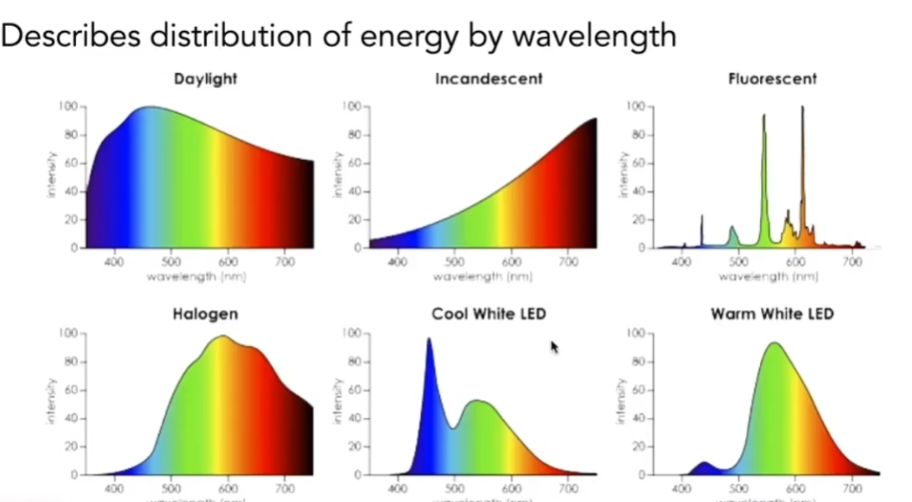
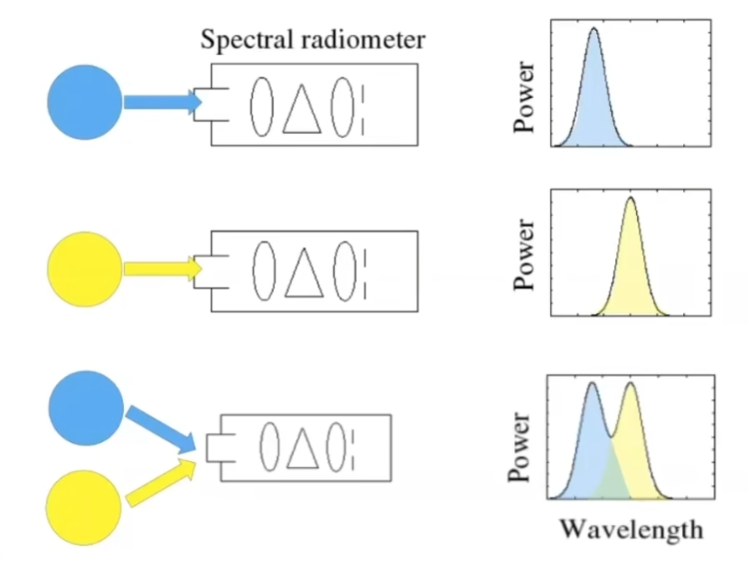
- SPD有线性的性质
What is Color?
- 颜色是人的感知,并不是物理上的一些东西
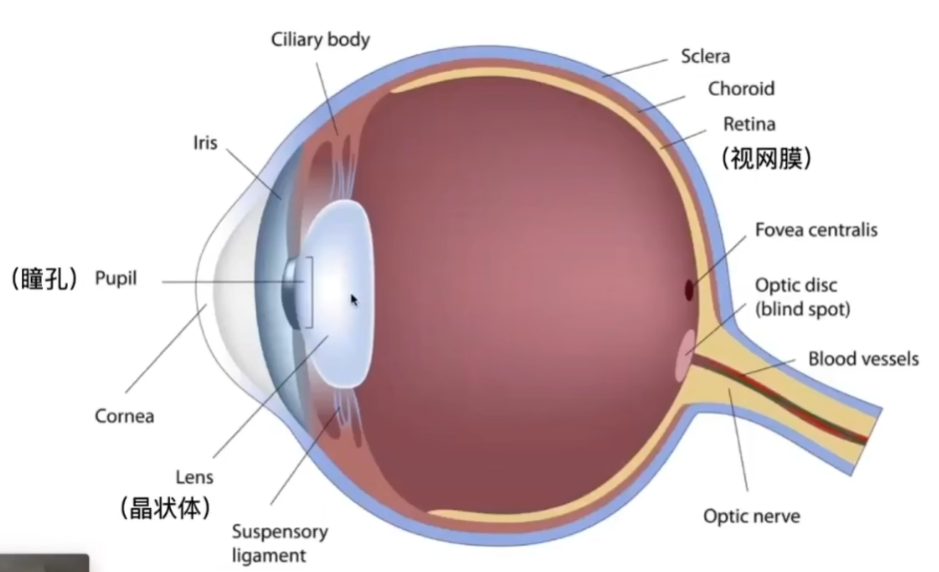
- 人眼就是一个摄像机
- 瞳孔可以调节大小,相当于光圈
- 晶状体相当于透镜,晶状体调节焦距,是通过肌肉来拽它
- 人眼感知的地方在视网膜上,也是最终光线到达的地方
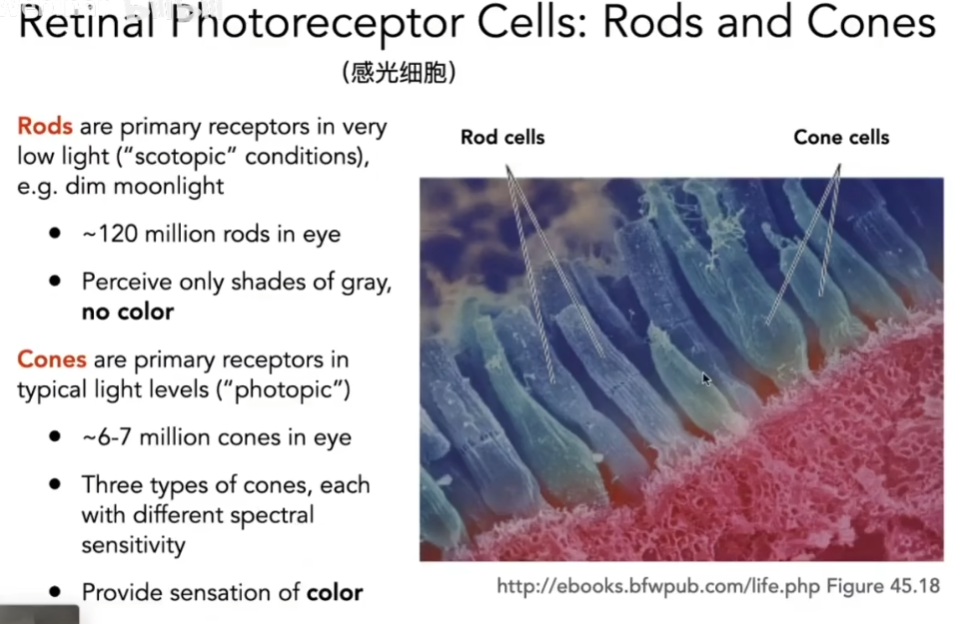
- 视网膜上有感光细胞
- 一种是棒状细胞:感知光的强度,但不感知颜色,用它可以得到灰度的图
- 一种是锥形细胞:比棒状细胞少很多,用来感知颜色
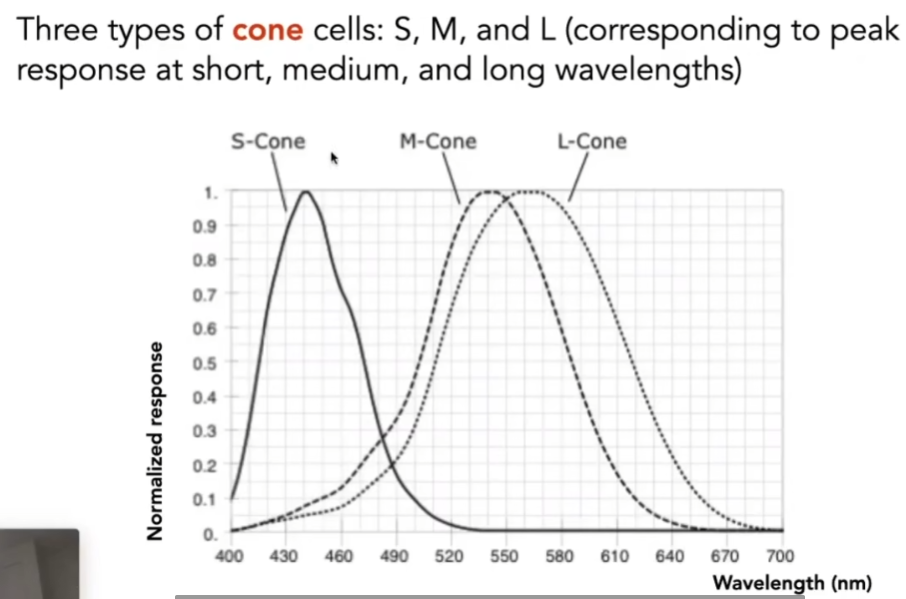
- 锥形细胞内部,又分成三种不同的锥形细胞(S、M、L类型的细胞),对三种类型的波长的响应各不相同
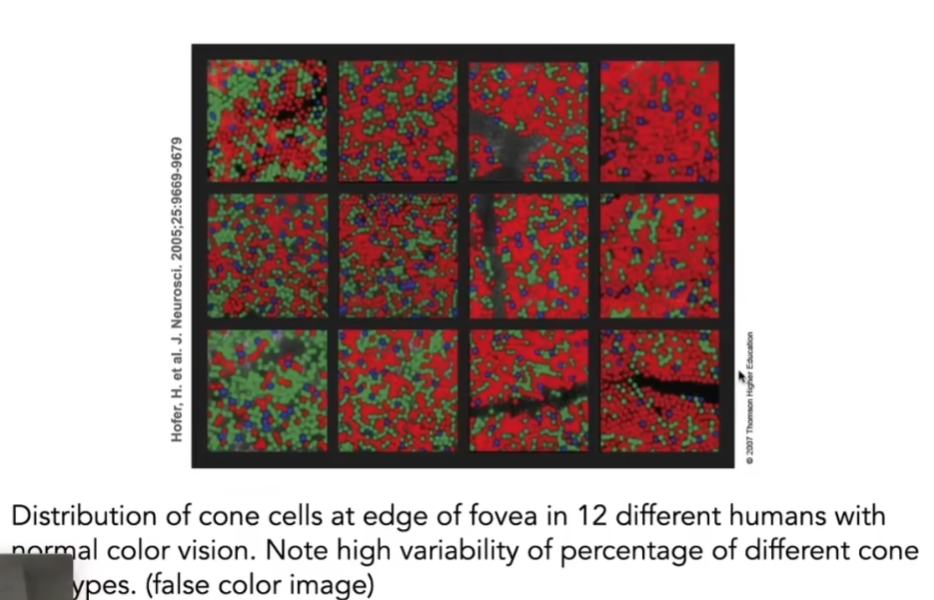
- 但是不同的人眼睛里这三种细胞的分布非常不一样
- 再次印证了颜色是人感知的结果
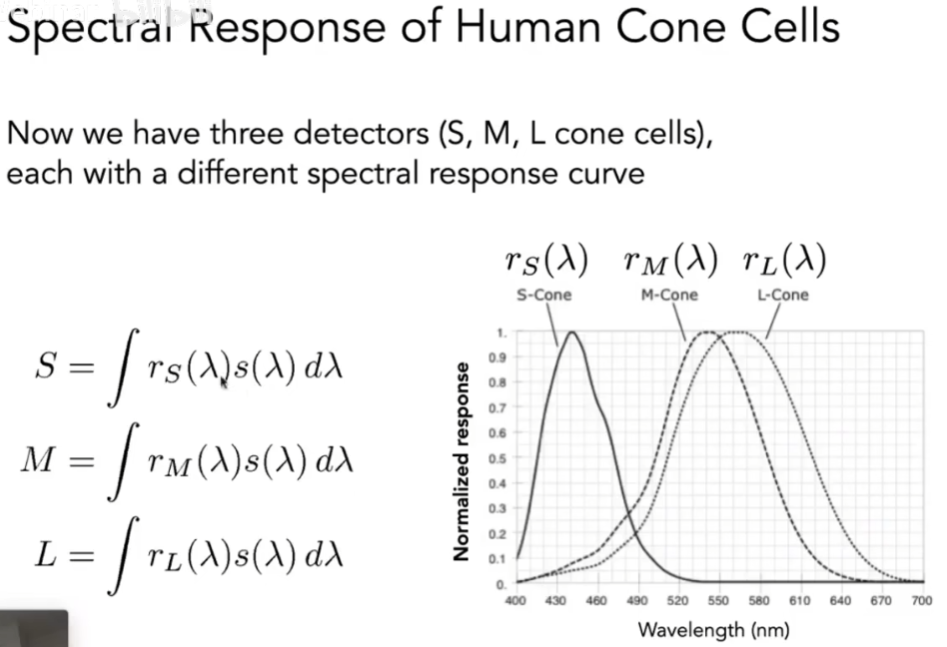
- 把光线的强度和相应的感知曲线的感应强度乘起来,再把每一个不同的波长都考虑进去,就是最终的结果

- 三种不同的感知细胞,会感应出三种颜色结果,这三个数才是真正看到的颜色,而不是光线本身的SPD
Metamerism(同色异谱)
- 不同的信号积分后得到相同的结果,是有可能发生的现象,称为同色异谱
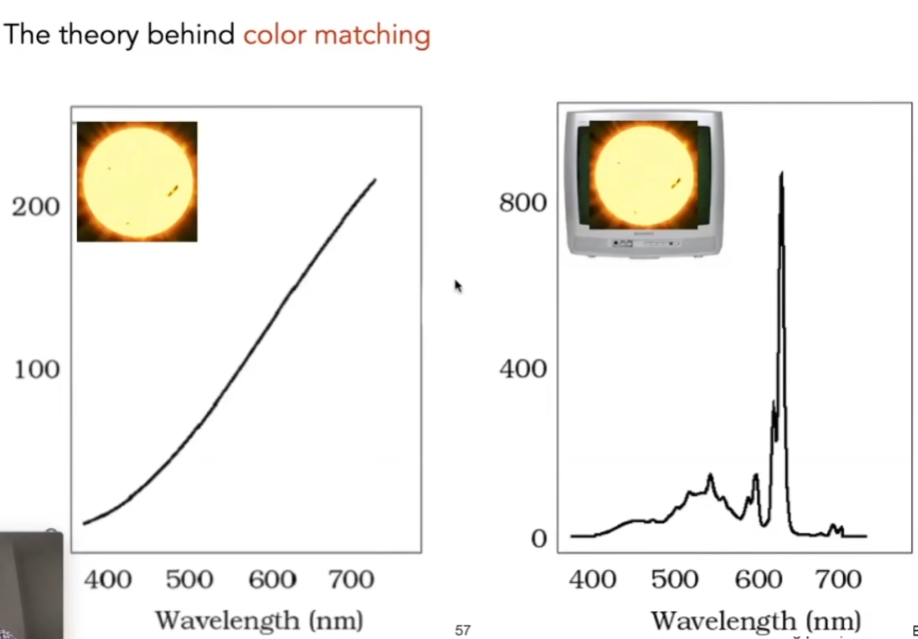
Color Reproduction / Matching
颜色应该如何混合

- 加色系统
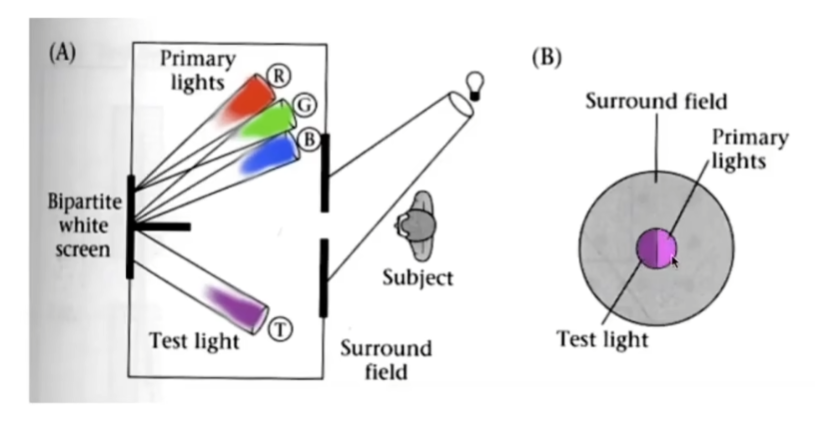
- 允许线性组合基本颜色来匹配任何给定的颜色
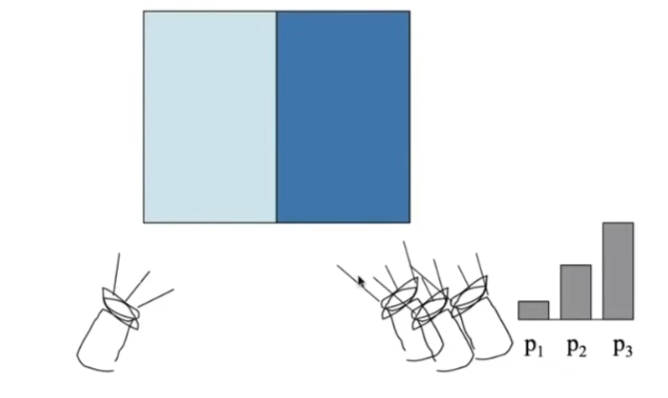
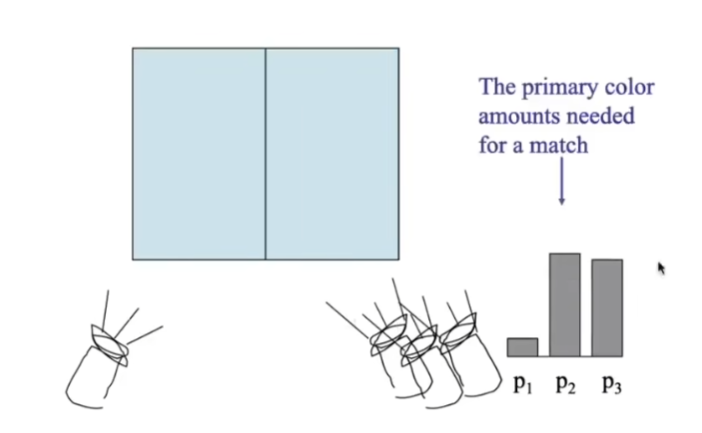
- 表示用多强的第一、二、三种颜色可以混合出左边的颜色
- 对任意的颜色都可以通过类似的方式解决
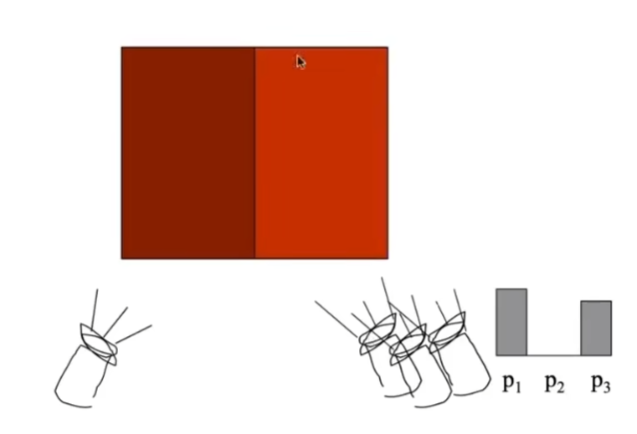
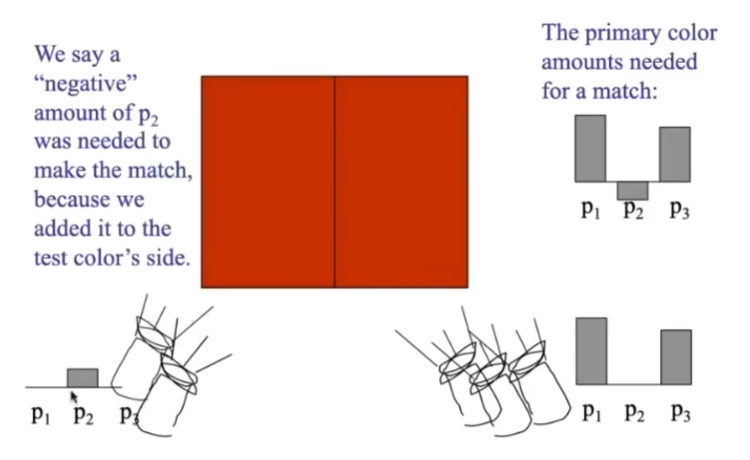
- 但是有一些情况不同,左边的颜色右边怎么混合都出不来
- 可以把左边需要混合的颜色往上加一个颜色,相当于对应右边减掉一个颜色,这就是线性的性质
- 通过几种颜色混合出一种颜色,系数是负的是没有关系的
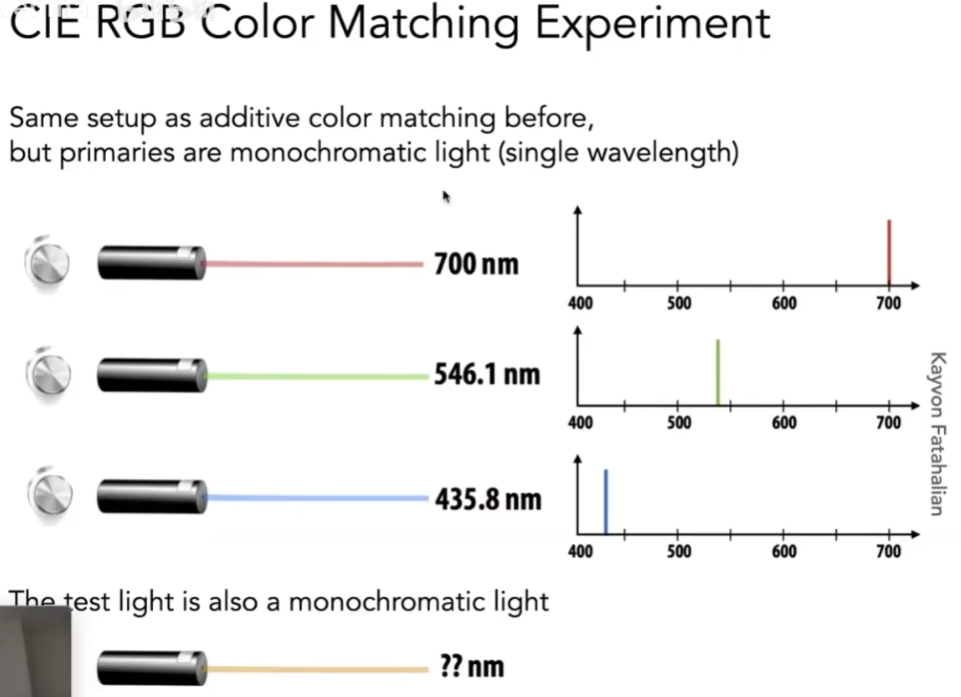
- CIE(一个组织)定义了RGB系统,它要做颜色匹配
- 给定任何一个颜色,是单波长的一个颜色激光,光线的SPD就是一个单一的函数
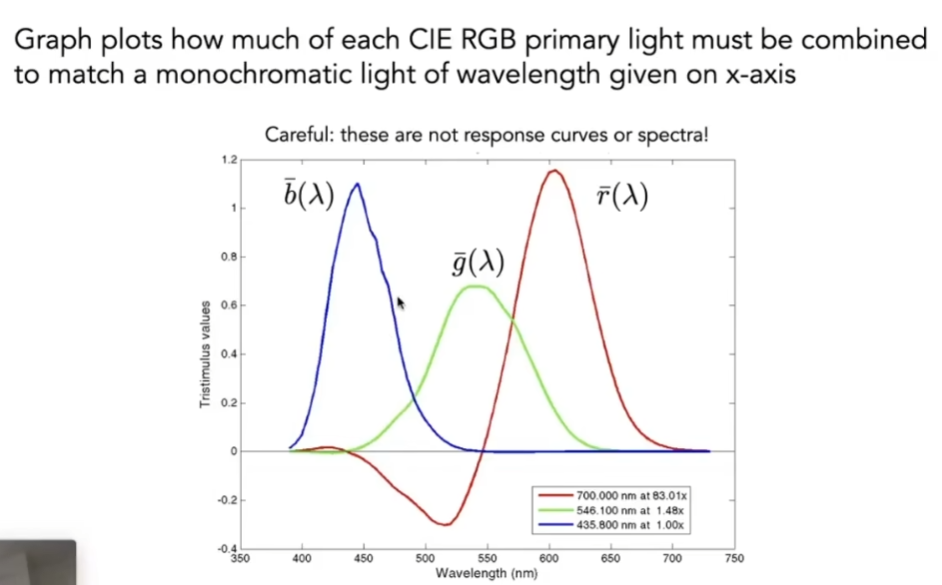
- 混合各种不同的单色光,得到任何一个波长上的给定的光线颜色
- 叫做匹配函数(CIE RGB Color Matching Functions)
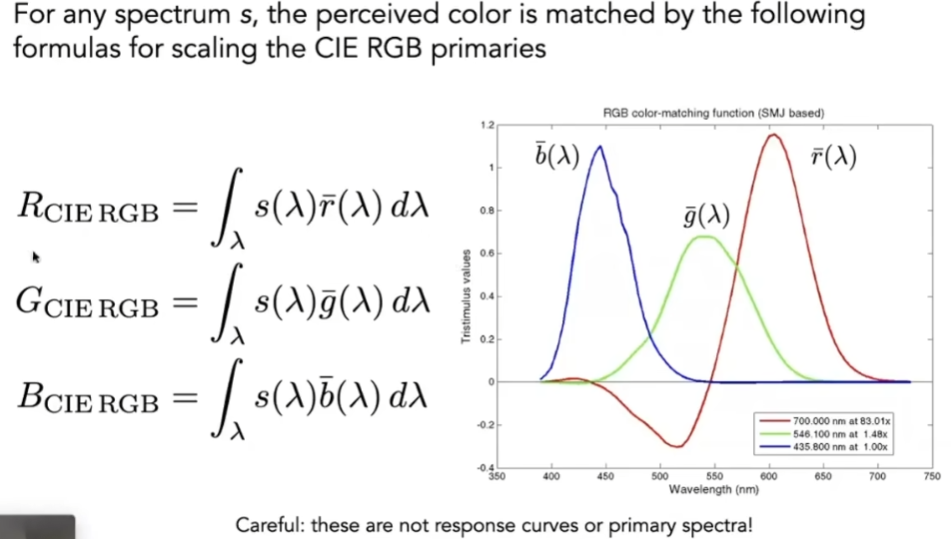
- 如果给定任何一个实际的SPD分布,需要考虑每一个波长用多上的红色、绿色、蓝色混合才能得到它,自然是一个积分的结果
Color Space

- 标准RGB系统是广泛使用的一个标准系统
- 但是它所形成的色域是有限的
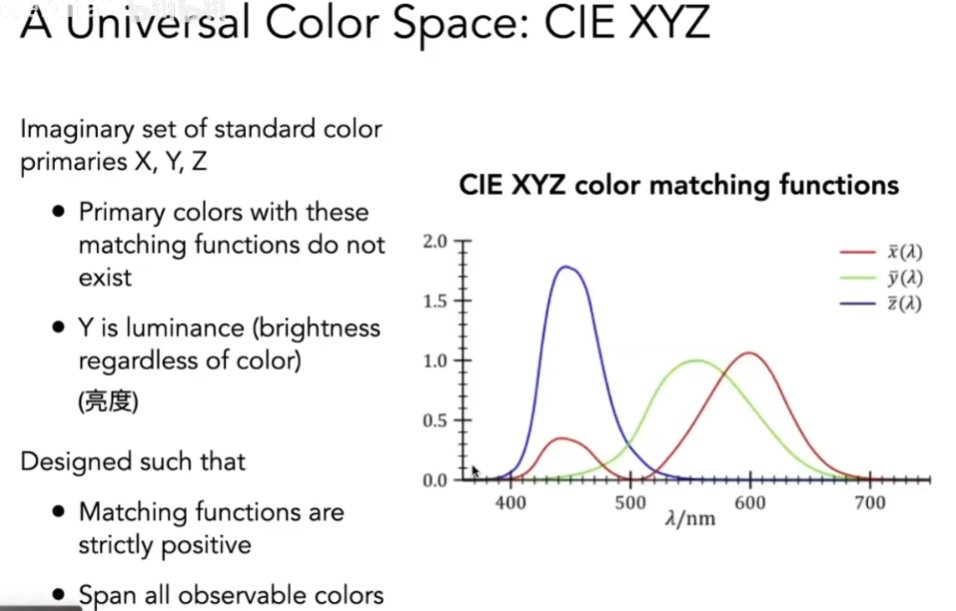
- CIE XYZ系统是在科学上更加广泛应用的一个系统
- 同样要定义颜色匹配函数
- 它不是实验测出来的,是人造的颜色匹配函数
- 绿色的曲线覆盖波长非常均匀,分布是对称的,正常来说用x、y、z三个匹配函数匹配出不同的颜色得到的Y(类似于RGB的G)一定程度上就可以表示亮度
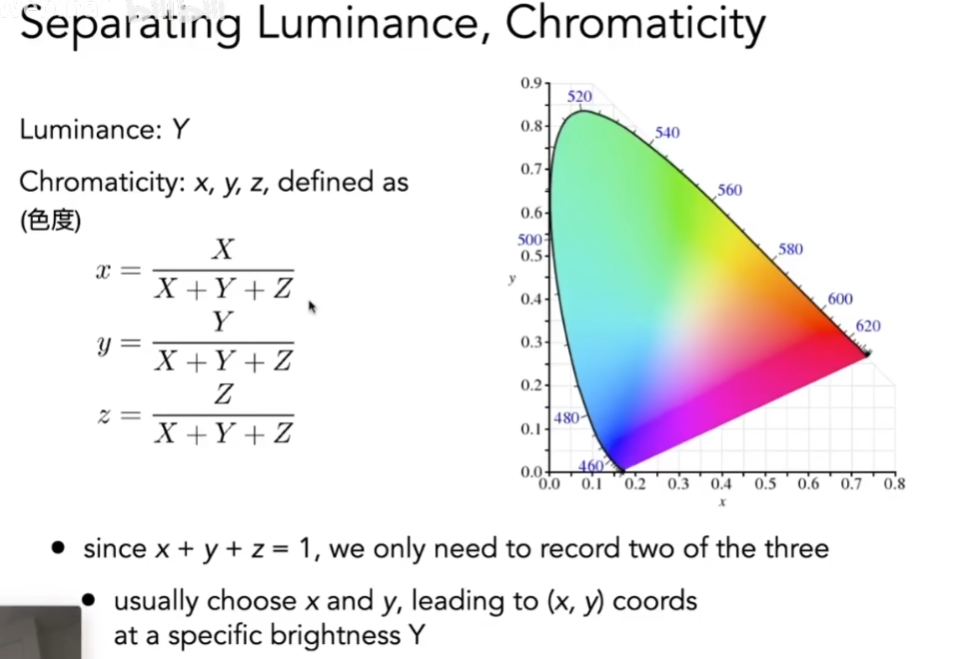
- 把XYZ系统,能够表示的所有的颜色都显示出来
- 而XYZ是三维的,不好可视化
- 只想显示其中的两维
- 对任何的XYZ先做一个归一化,得到三个归一化的值xyz,由于知道xyz相加等于一,所以只需要表示xy就行
- 为了显示x和y,它其实表示的颜色还是由XYZ来定的,其实还是三个变量
- 既然知道Y表示亮度,可以把亮度固定成某一个数,让X和Z发生变化,这样x和y都是X、Z的函数
- 这块区域就叫做色域,也就是所有一个颜色空间可以显示的颜色
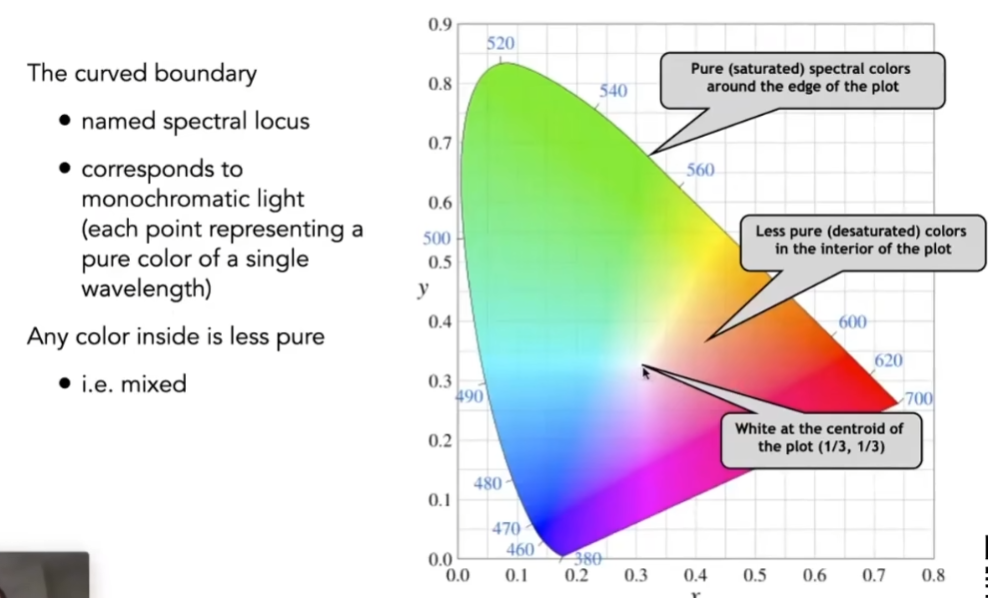
- 对于一个色域来说,中心呈白色,是由各种颜色混合而来,说白色是最不纯的颜色,而纯的颜色都在边界上
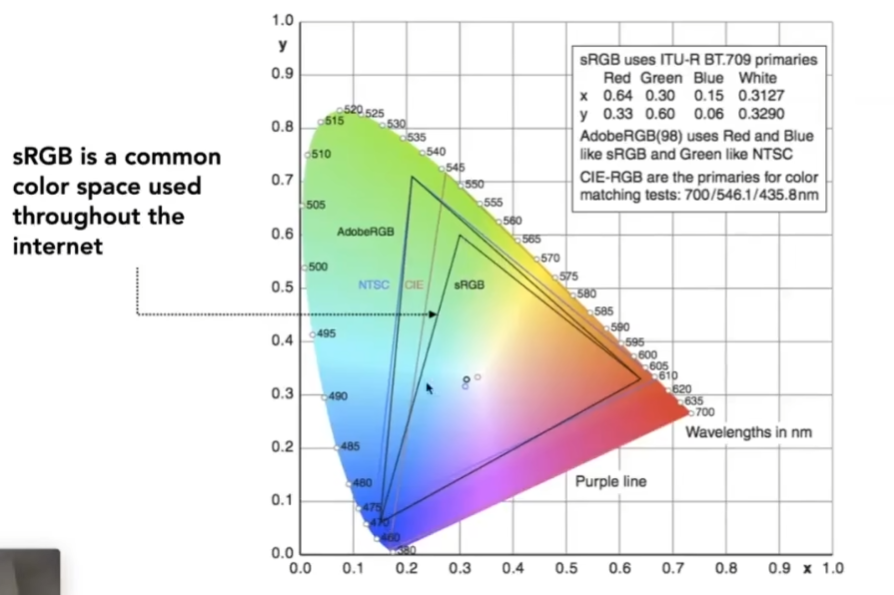
- 不同的颜色空间,表示的颜色范围是不一样的
Perceptually Organized Color Space
HSV颜色空间
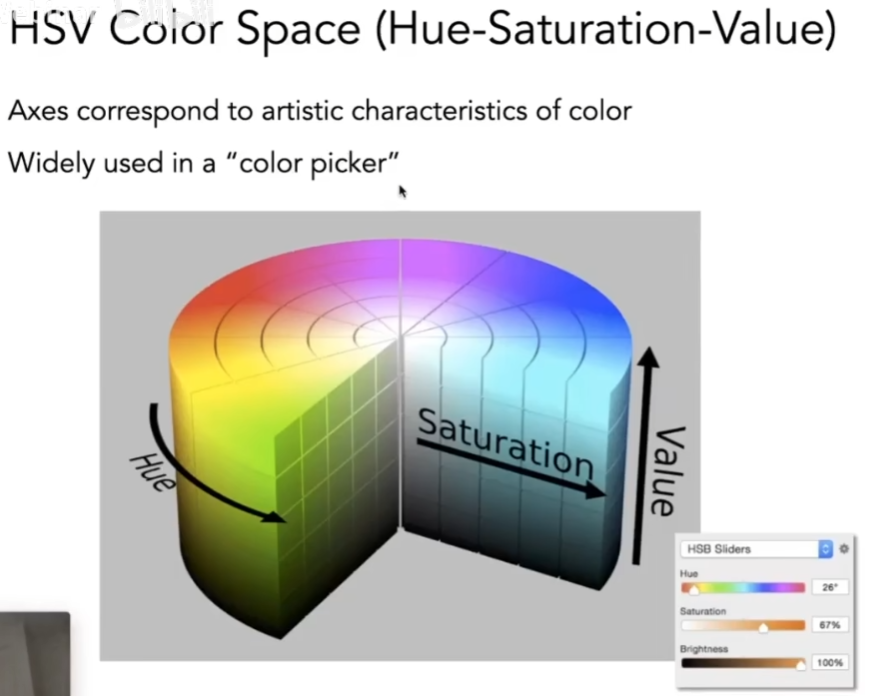

- 允许选择不同的色调(Hue)、饱和度(Saturation)、亮度(Brightness/Value)
- 色调:不同类型的颜色
- 饱和度:更接近白色(不纯)还是颜色本身的纯色,越饱和越接近单一的颜色
CIE LAB Space
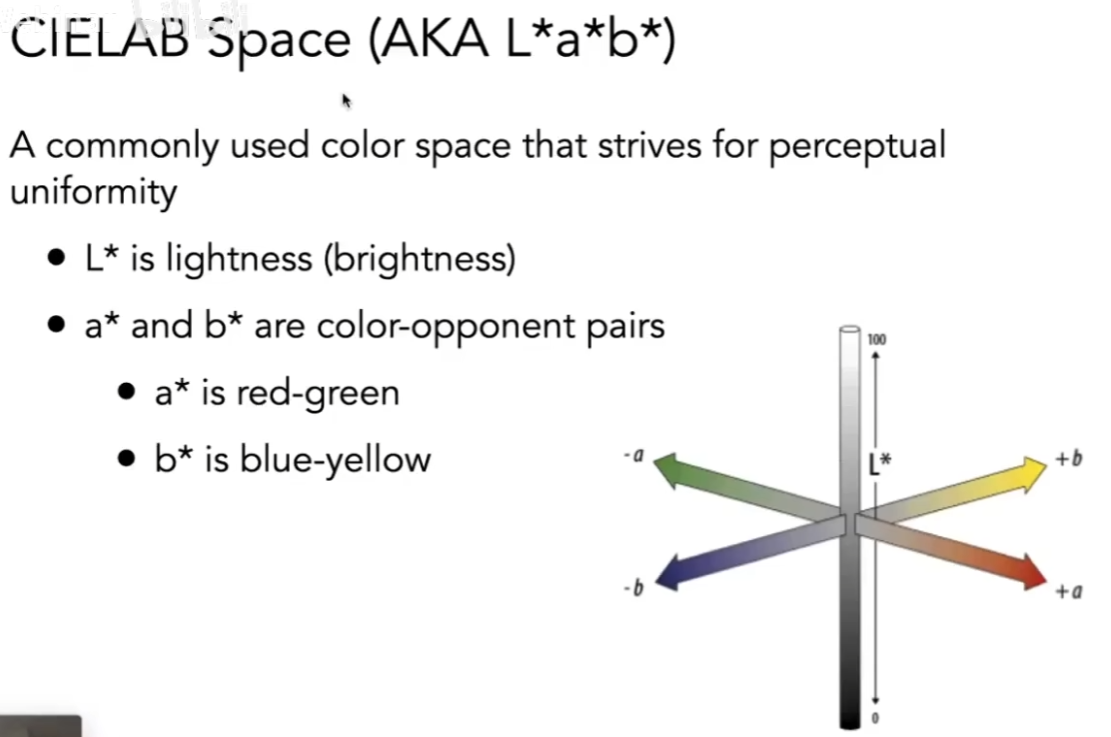
- 也是跟感知有关
- L轴是亮度
- a、b轴相互垂直,a轴表示红和绿,b轴表示蓝和黄
- 它认为任何一个轴上表示的颜色,它的极限(两端)都是互补色

- 比如能想到深绿、黄绿、蓝绿,但不会想象一种偏红的绿
- 人的大脑对互补色有一个定义,人脑会自动把互补色补上


- 颜色本身是感知,有些事情是相对的
减色系统

- 各种颜色混合后会得到黑色
- 为什么需要K? –考虑印刷成本,因为黑色墨水便宜,彩色墨水贵,需要黑色的时候直接用黑色墨水而不用混合
- XYZ有非常好的理论性质,非常大的色域
- RGB好用,很直观
- HSV比较好调颜色
Lecture 21 Animation
对动画的不同理解

- 让物体”活”起来
- 用于交流的工具,给别人展示各种动起来的东西
- 早期的动画人们并不关心画的对不对,是否符合物理,只要看起来差不多对,那就差不多
- 也可以理解成建模、几何的拓展
- 动画无非是在不同的时间(帧)有不同的几何形状,动画就是为了得到这些不同的形状要怎么去计算
- 动画的形成是把很多的图按顺序、按一定的速度去播放,就可以了
- 不同的应用对动画的要求是不一样的
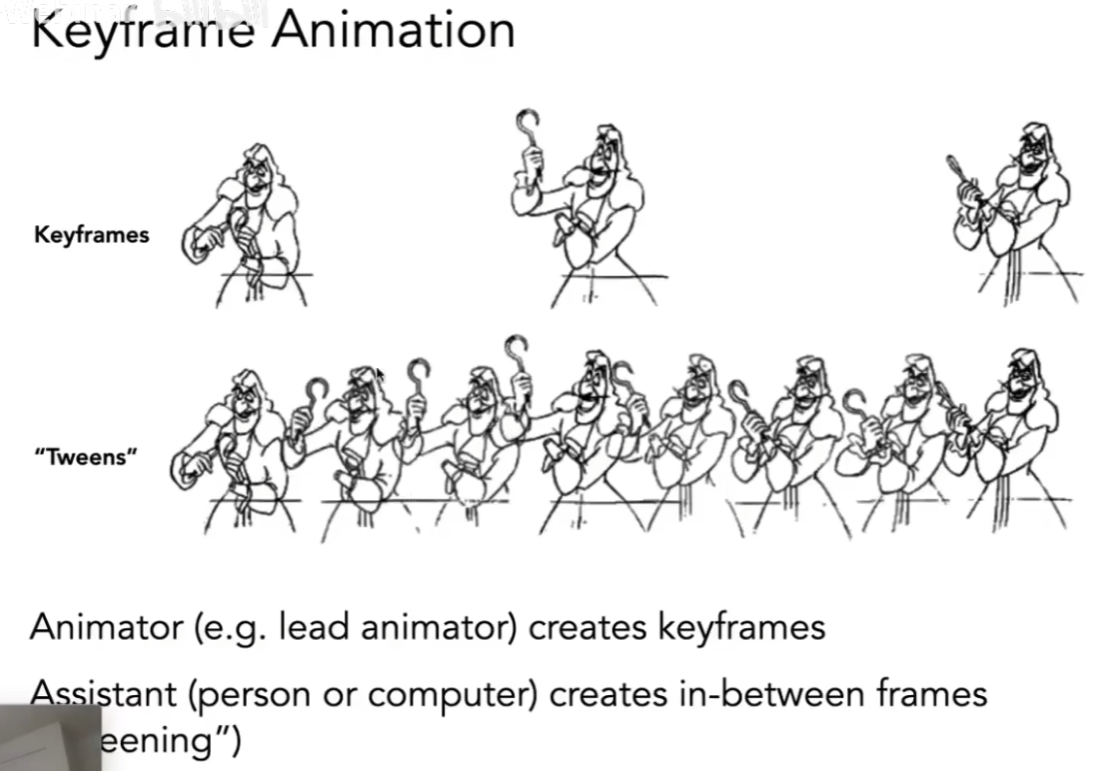
- 关键帧
- 工作量大
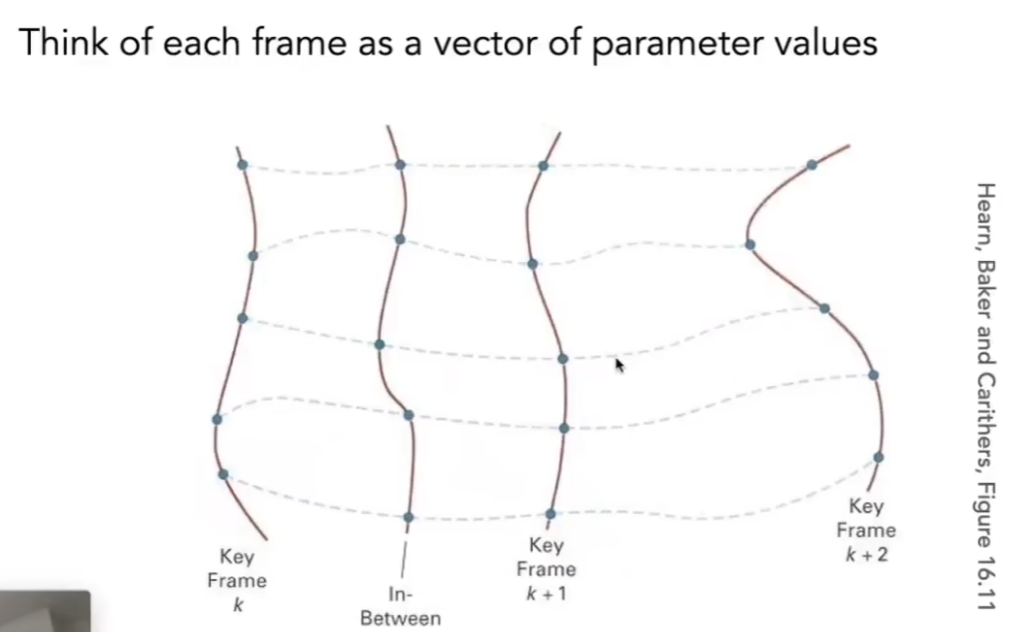
- 关键帧动画本质是插值的技术
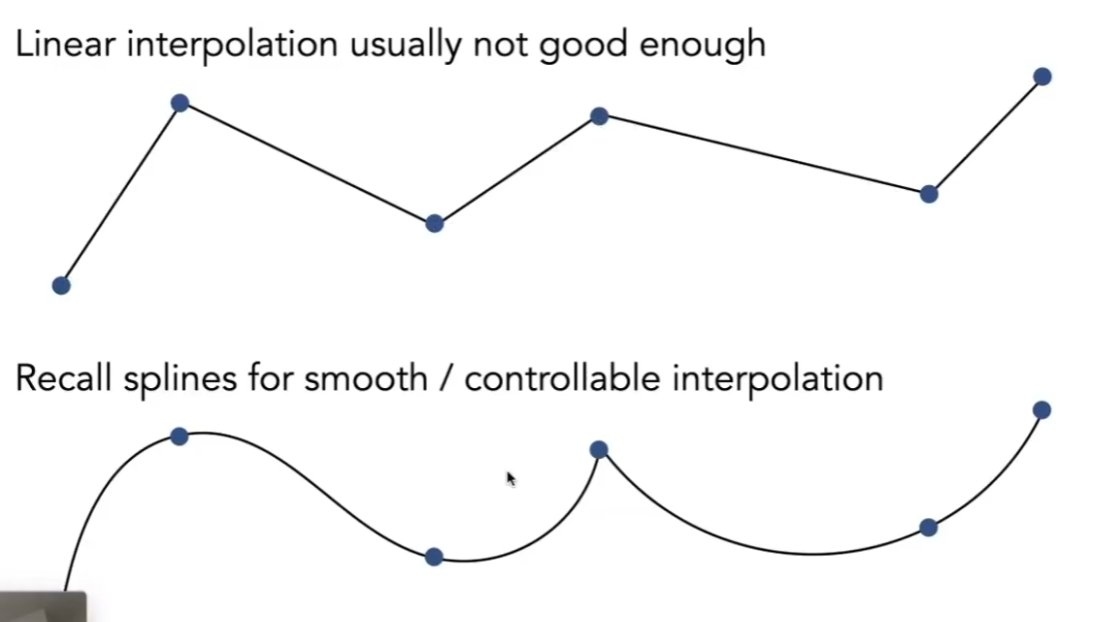
- 希望有种东西可以控制插值效果,这时虚线/样条是非常重要的
- 动画和几何是关联的
Physical Simulation (物理模拟/仿真)

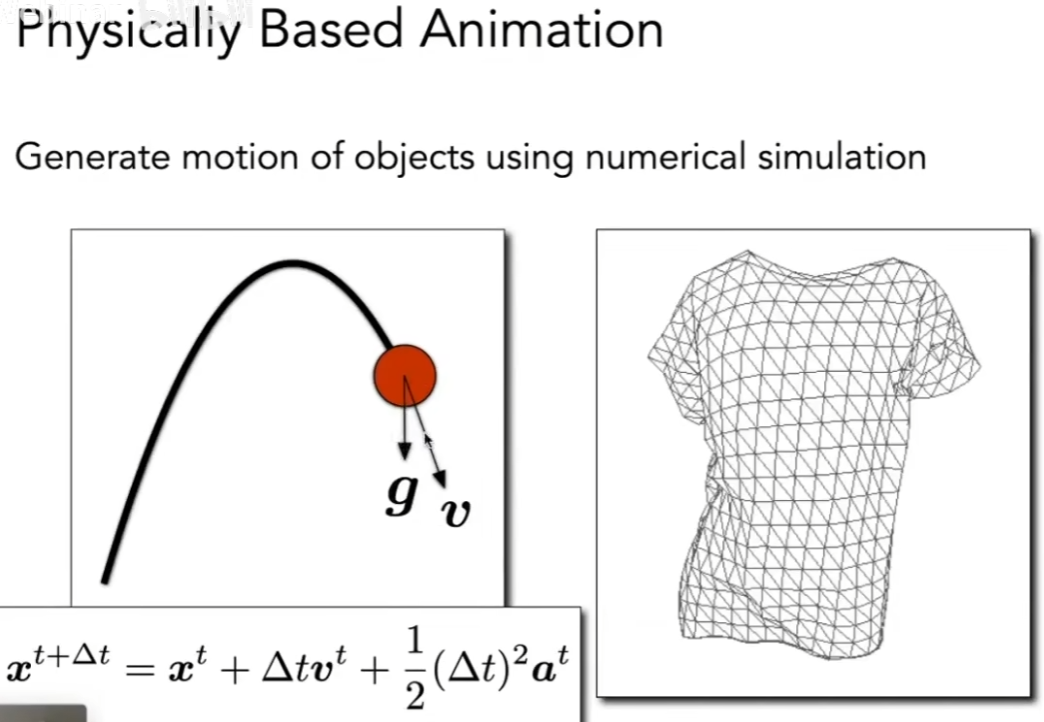
- 物理模拟说的就是推导、实现、利用不同的物理公式,来计算出一个物体应该有什么形状/位置上的变化
Mass Spring System (质点弹簧系统)

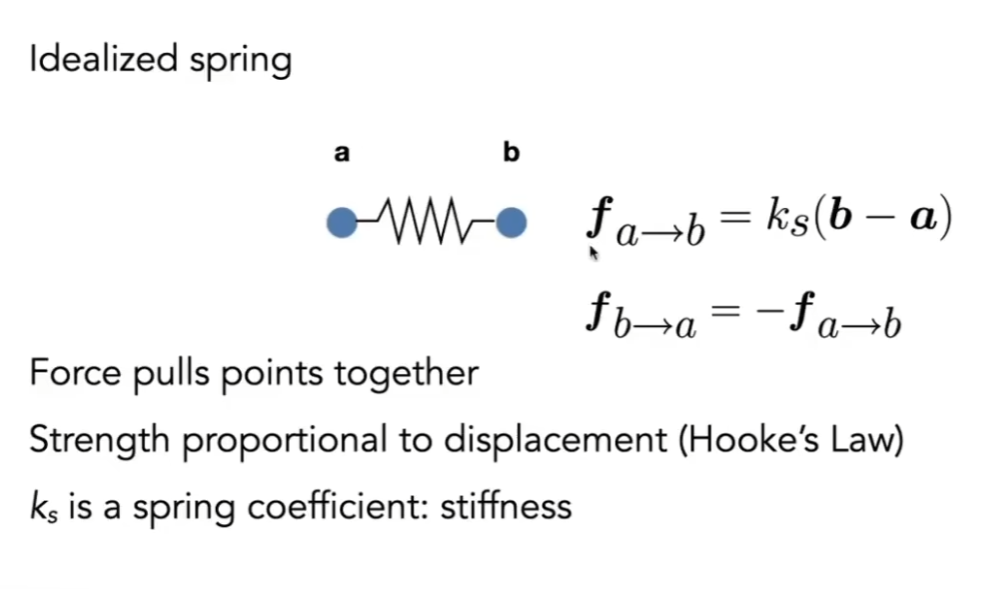
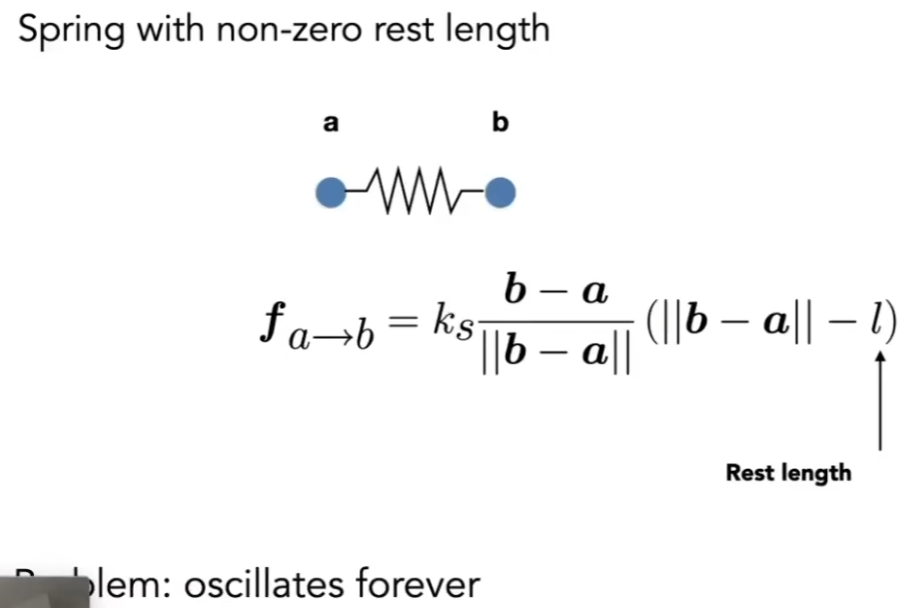
- ||b - a||表示方向
- 问题:永远弹下去
- 解决:加个摩擦力(damping force)
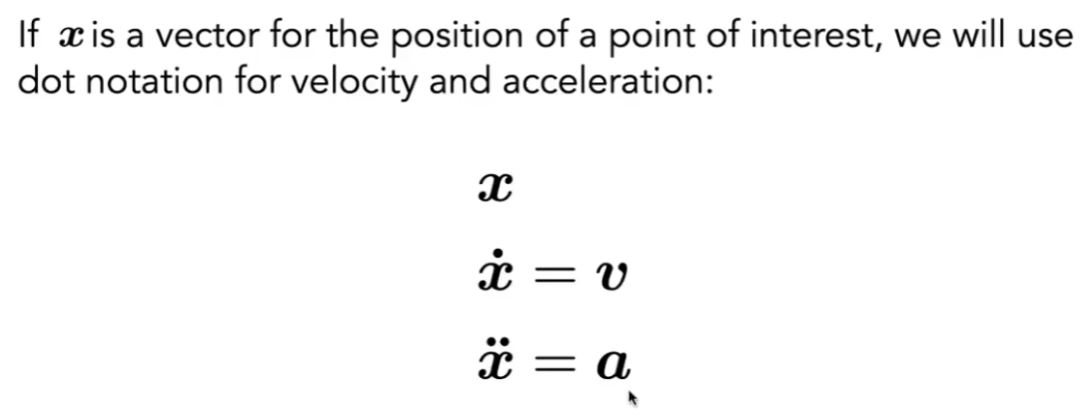
- 在模拟仿真中,用x一点表示一阶导数(速度),两点表示二阶导数(加速度)

- 会引起所有的运动都停下来

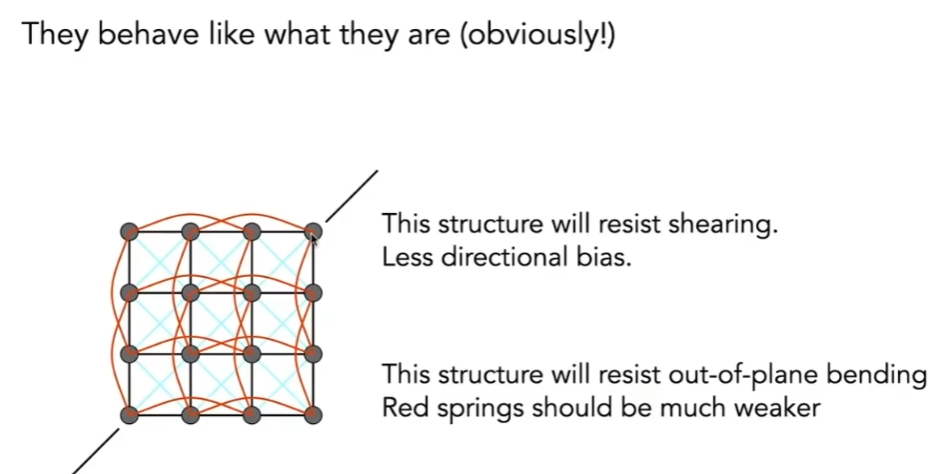
Particle System
- 本质上是定义个体与群体之间的关系
Forward Kinematics
- 在图形学中通常把运动学区分成正向的和反向的
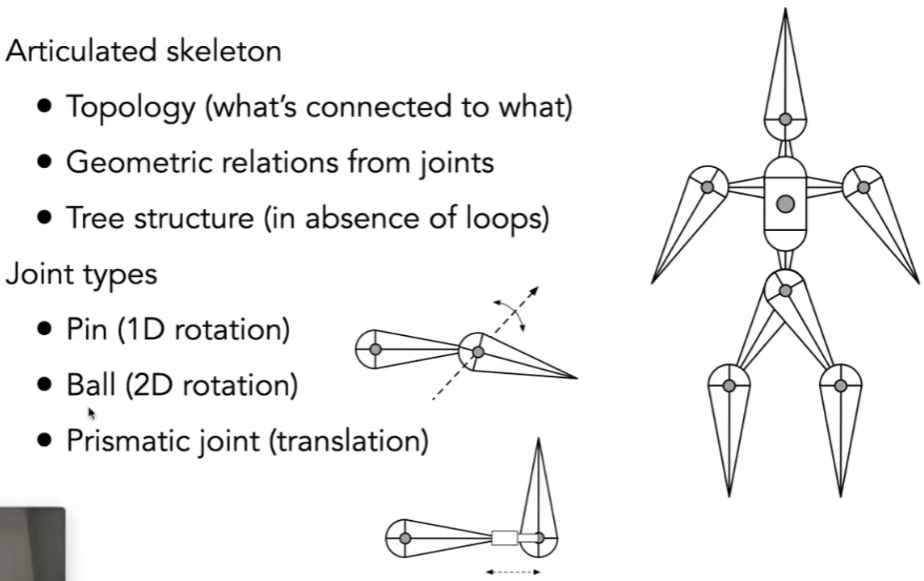
- 定义一些简单的关节模型,形成一个复杂的模型
- 本身又能把整个结构形成加速结构/树形结构
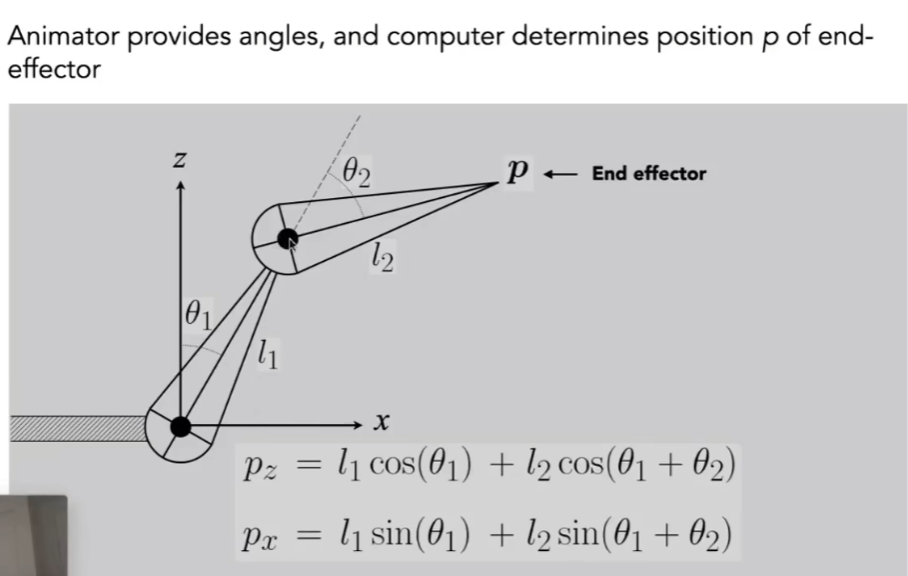

- 运动学定义的东西都非常物理,而艺术家喜欢直接拿着骨骼到处拽,不用通过调整角度来控制骨骼,引入了逆运动学
Inverse Kinematics

- 计算复杂、解不唯一或无解都有可能发生
Rigging

- 蒙皮、插值
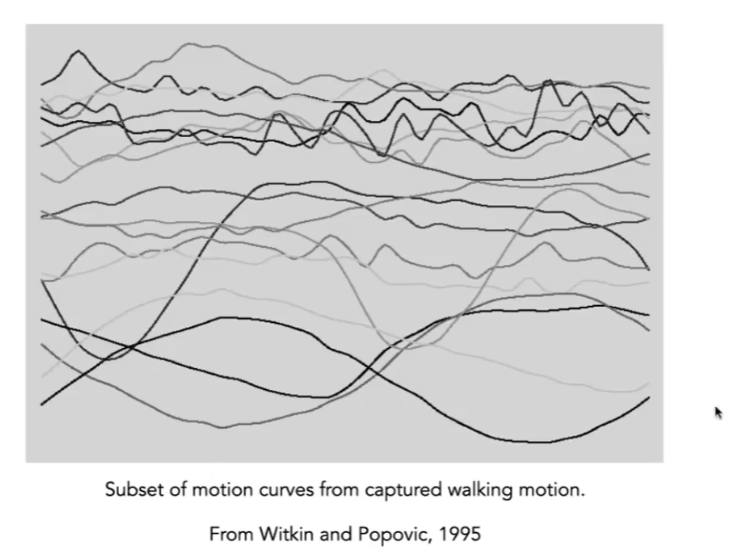
Motion Capture(动作捕捉)





Lecture 22 Animation Cont.

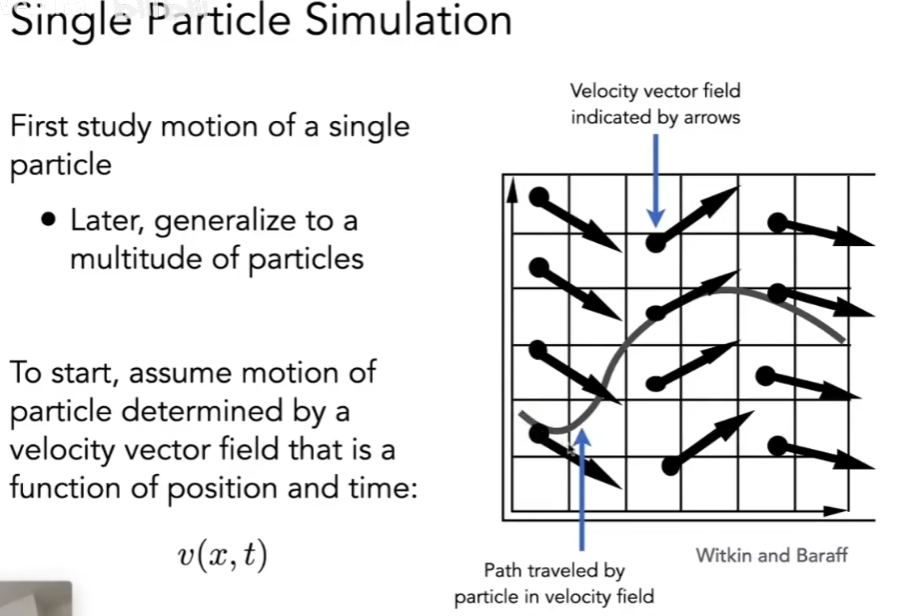


- 显式/前向 欧拉
- 非常不稳定
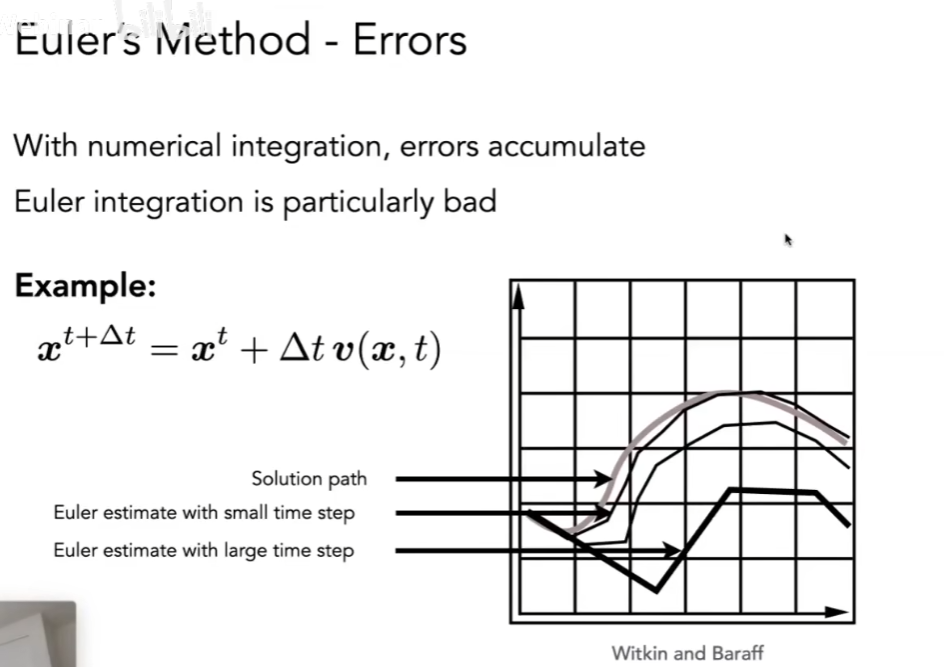
- 误差可以通过减小步长缩小


Combating Instability

- 中点法
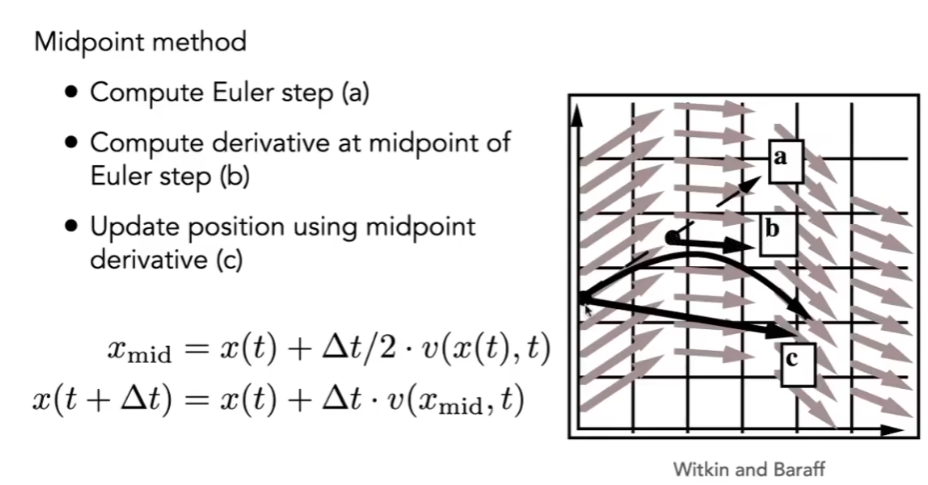

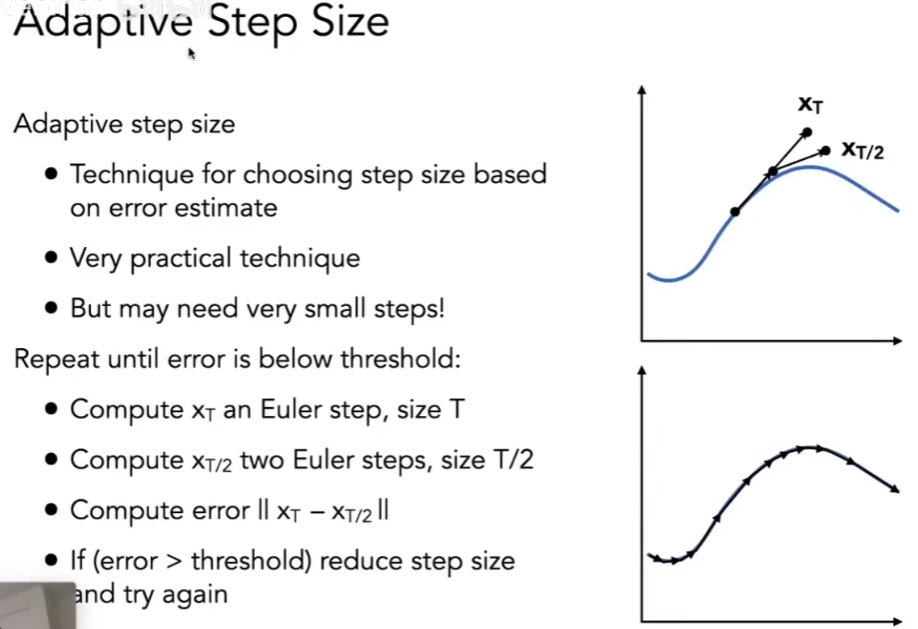
- 自适应思路,试着把时间分成两半,如果跑出来结果接近就不往下分,反之往下分

- 隐式欧拉方法

- Runge-Kutta方法,简称RK4
- 龙格库塔方法是一系列方法

- Position-Based / Verlet Integration
- 通过调整位置,使得最终能能够满足某些限制

刚体

- 位置、朝向、速度、角速度

