前言
- 由于内容过多,做笔记太费时间,对Games202只做简单记录
Lecture 1
- “怨虎龙都没打过你还来听什么网课,本末倒置” -by 闫令琪
Lecture 2 Recap of CG Basics
Basic GPU hardware pipeline
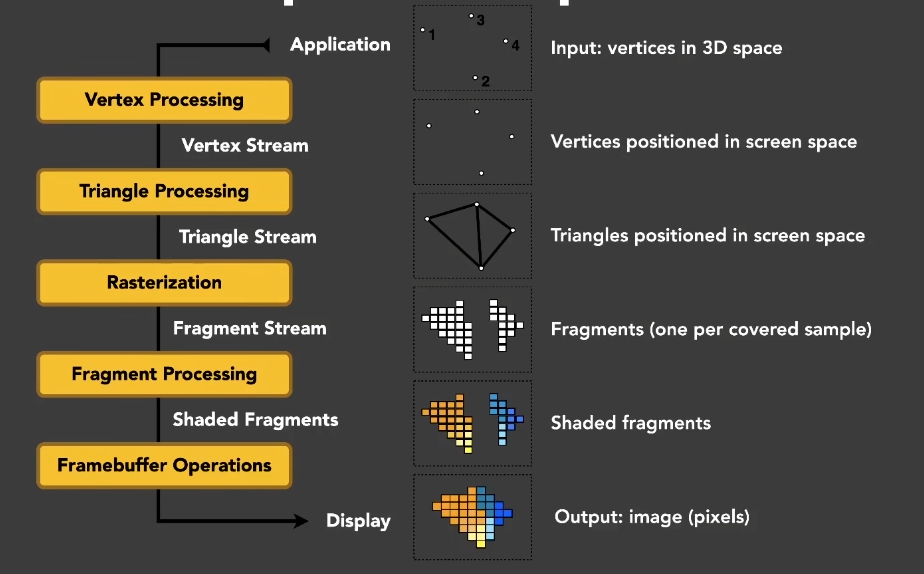
- 渲染的过程:开始是3D模型,最后是一张图
- 中间过程:渲染管线(渲染流水线)
- 物体在空间中被表示成点和它的连接关系
- 任何的点都会经过顶点的处理和变换(MVP),最后成为屏幕上的点
- 经过一系列的变换后,它们的连接关系并没有发生改变,仍然会表示那么些三角形,只不过这些三角形被投影到屏幕上去了
- 三角形被投影到屏幕上去了,下一步做光栅化(“光栅化”最早的词就是”画”),就是把原本连续表示的三角形给连起来,把它离散化成屏幕空间上的一堆像素(fragments)
- 在打散成像素的过程中,会涉及到一些遮挡的处理
- 确定了可见的fragment后,就可以对它们进行着色,就是去计算它们应该长什么样(Bling-Phong)
- 先判断片段的顺序,考虑遮挡,还是先做着色,有不同的处理方法,有细微的差别,影响不大
OpenGL
- OpenGL是什么
- 是一系列的API,在CPU端执行的,它负责调动GPU
- 因此,用什么语言都没有关系,我们更关心GPU怎么执行,而不是CPU怎么让GPU执行
- 特点:跨平台
- 确定:版本碎小;C风格的代码,没有面向对象一说,对编程人员来说不方便;若干年前不好Debug
- 怎么用OpenGL
- 类比:把整个的渲染过程理解成画一幅油画的过程
- a.把物体放好
- b.把画架放好
- c.放置画布
- d.在画布上画东西
- e.(放上另一个画布继续画)
- f.(用以前的画做参考)
- 类比:把整个的渲染过程理解成画一幅油画的过程
- A.放置物体/模型
- 什么物体
- 怎样摆放
- Vertex buffer object(VBO)
- User specifies an object’s vertices, normals, texture coords and send then to GPU as a Vertex buffer object(VBO)
- VBO就是GPU中的一块区域,这块区域用来存储我们的模型
- Very similar to .obj files
- Use OpenGL functions to obtain matrices
- e.g., glTranslate, glMultMatrix, etc.
- No need to write anything on your own
- B.放置画架
- 视图变换
- Create/use a framebuffer (类比OpenGL里的画架)
- Set camera by simply calling, e.g., void gluPerspective(GLdouble fovy, GLdouble aspect, GLdouble zNear, GLdouble zFar)
- OpenGL让一切都得到简化,只需要规定相机的一些属性(e.g.,可视角度fovy、长宽比aspect、近平面zNear、远平面zFar)
- C.固定画布
- 对场景渲染一次,相当于坐在画架前画,但是可以画很多幅不同的画
- 即用一个framebuffer,可以指定这个framebuffer它可以输出很多不同的纹理(shading, depth, etc.)
- 渲染一次(one pass)场景,可以得到很多不同的东西,由fragment shader告诉你最后要写到哪一个纹理上去
- E.可以用同一个画架画多幅画,只需要换一块画布
- 只要指定一个framebuffer,可以一下渲染出很多不同的纹理
- D.在画布上画画
- 顶点/片元着色器
- 对每一个顶点进行操作
- 写顶点着色器着色
- MVP映射、插值后,送给片元着色器
- OpenGL把一个三角形打成一堆像素
- 对每一个片元进行操作
- 写片段着色器着色
- F.Multiple passes
- Use your own previous paintings for reference
总结
- 我们更需要关心的是写顶点/片元着色器,其他更多的都是可封装的
- OpenGL做什么事情:就是告诉GPU该做什么,而且可以告诉GPU去做多次不同的任务
- OpenGL在渲染之前,一定要先告诉清楚信息给GPU
- 为了让场景能够渲染,要做的事情(in each pass):
- 定义要渲染的物体、场景,定义物体、场景的MVP矩阵,相机关系等
- 要选什么framebuffer(画架),framebuffer的输出是几个纹理
- 告诉GPU怎么渲染(顶点/片元着色器)
- 当所有东西都告诉GPU后,再拿去渲染
其他
- 垂直同步、双重缓冲、三重缓冲:先把渲染的结果存到一个纹理或一个缓冲区里去,当渲染好后,确保没问题,再拿到屏幕上显示
OpenGL Shading Language(GLSL)
The Rendering Equation
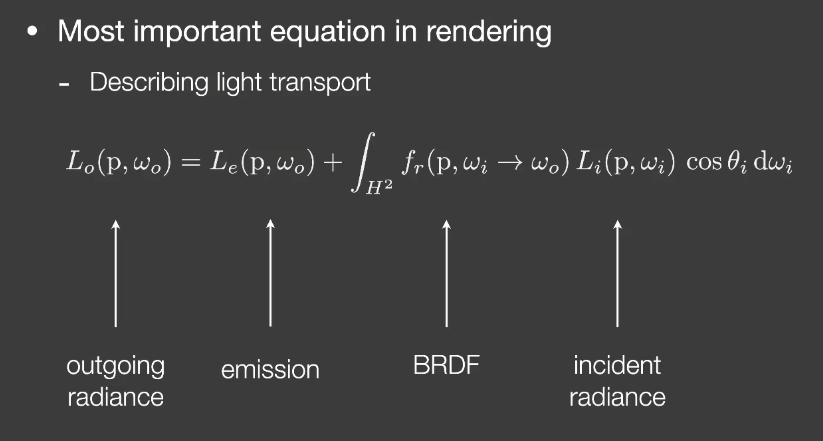
- 一套正确的用来描述光线传播的方法/等式
- 你看到的任何一个点p,观测方向O,是它本身发出来的radiance,加上所有其他打到这一点的radiance乘以BRDF乘以cos角度,把这些光收集起来
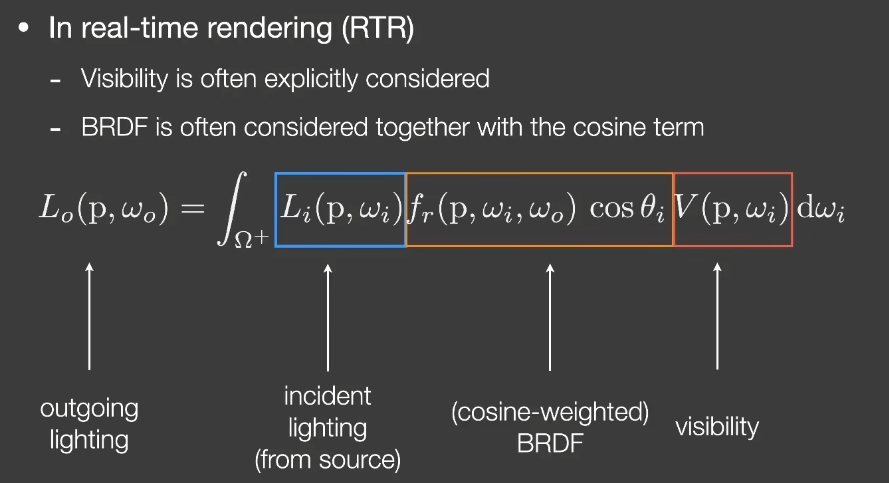
- 在实时渲染(RTR)中,说的BRDF有可能指BRDF,也有可能指cosine-weighted BRDF
- 人们会考虑当前这个shading point,它是否能看到四面八方的光照,会不会引入visibility的概念
Calculus
- 放在下节
Lecture 3 Real-Time Shadows 1
Shadow Mapping
- A 2-Pass Algorithm
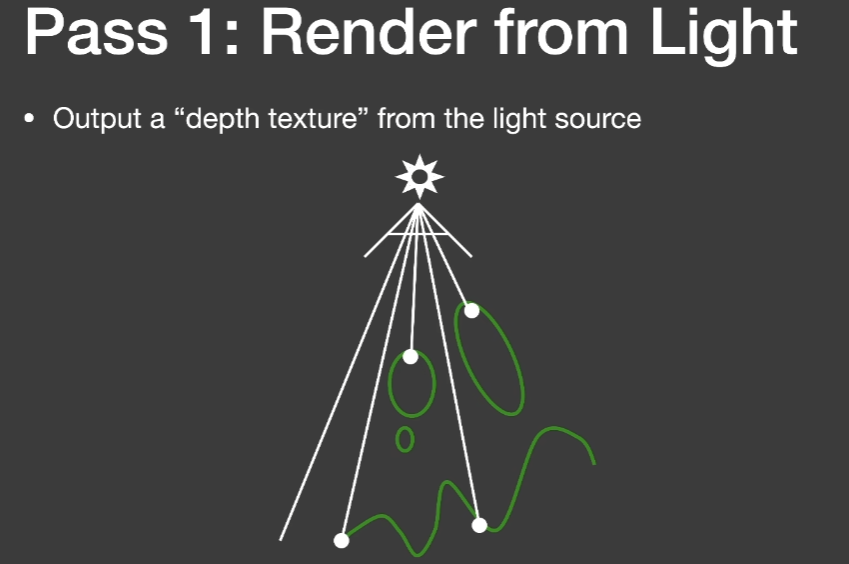
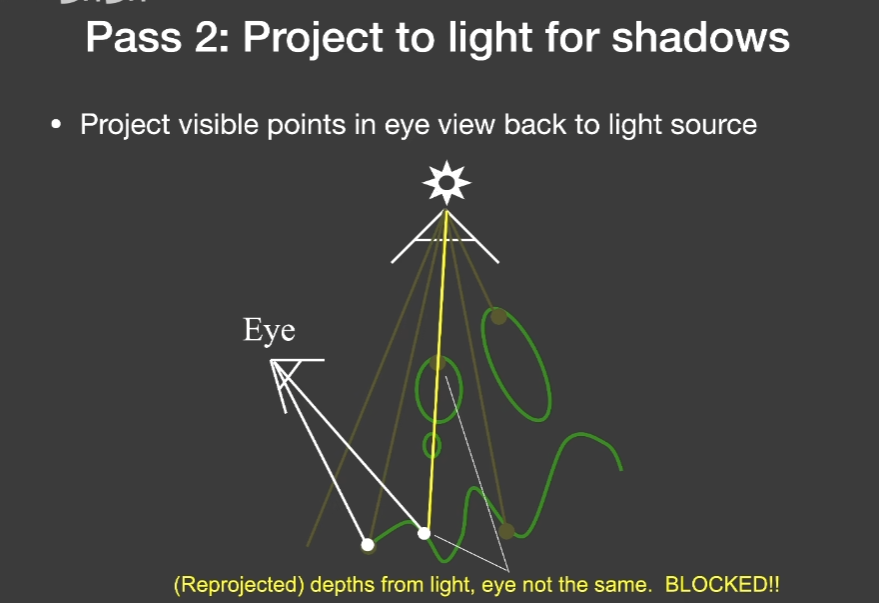
- 第一遍(Pass)渲染场景,会认为从light看向场景,并输出一个该light所能看到的最近的深度
- 有了这张ShadowMap之后,可以拿到后面去用。也就是第二遍Pass,从相机出发,真正地渲染场景,配合SM,可以去检测相机所看到的任何一点是否在阴影里
- An image-space algorithm
- 好处:SM生成了就可以作为场景中的几何表示,为了得到阴影只需要SM,不需要实际的场景的几何
- 坏处:会出现自遮挡、走样现象
- Well known shadow rendering technique
- 家喻户晓的算法
- 最早的时候在离线渲染也是非常有用的生成阴影的方法
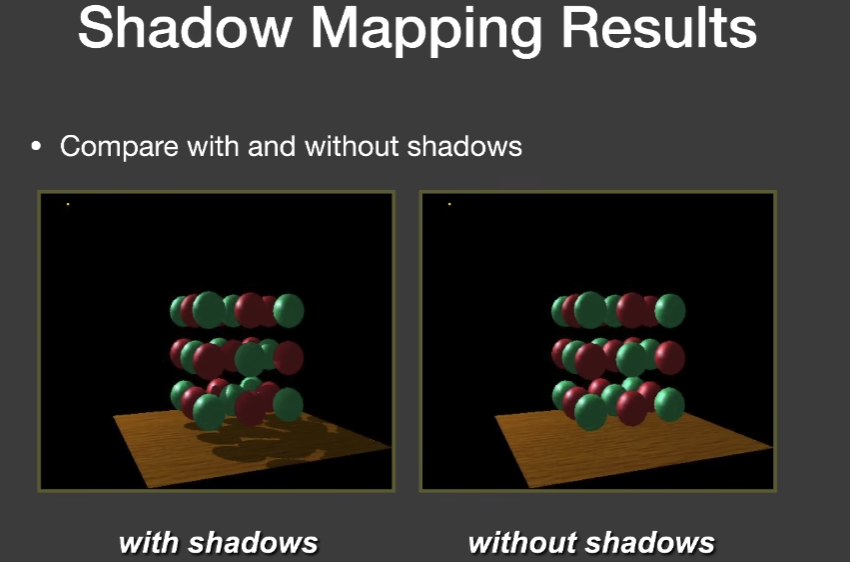
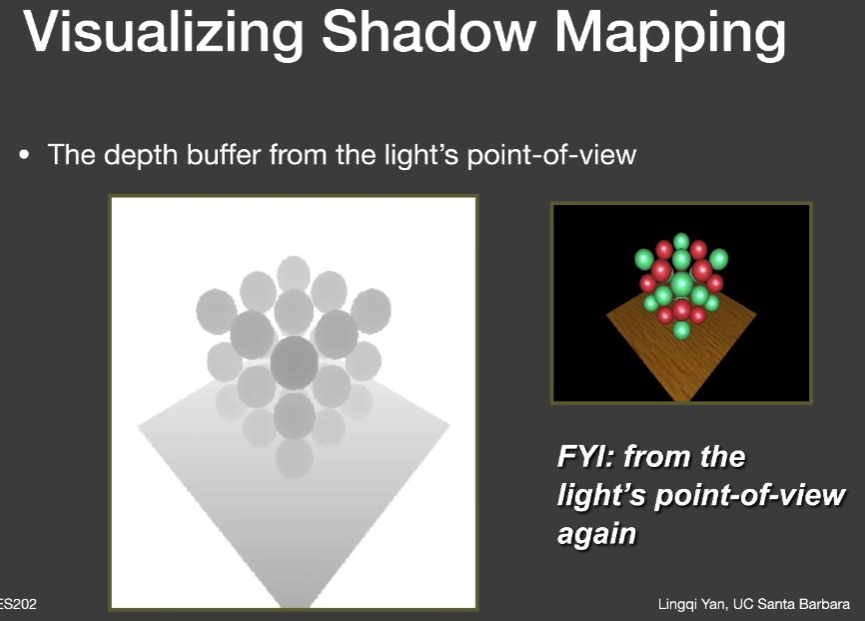

- 由于数值精度造成的地板纹路
- ShadowMap有精度,每个像素要记录它所看到的最浅深度,也就是说一个像素内是一个常数,一个像素对应的地板上的一块区域在ShadowMap看来是与成像平面平行的,所以会出现自遮挡现象
- 只有光线垂直照射平面的时候,不会出现自遮挡现象
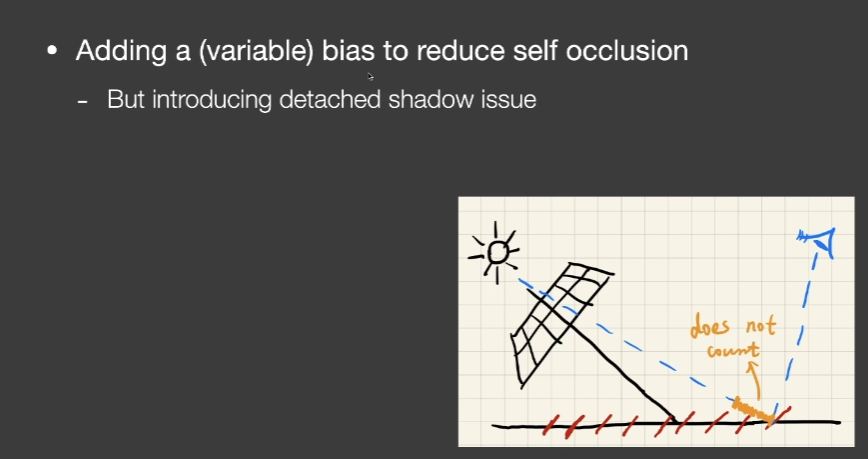
- 可以加上一小段bias去降低自遮挡情况,光源与地板垂直时bias小,夹角越大bias越大

- bias过大可能会造成丢失阴影的问题
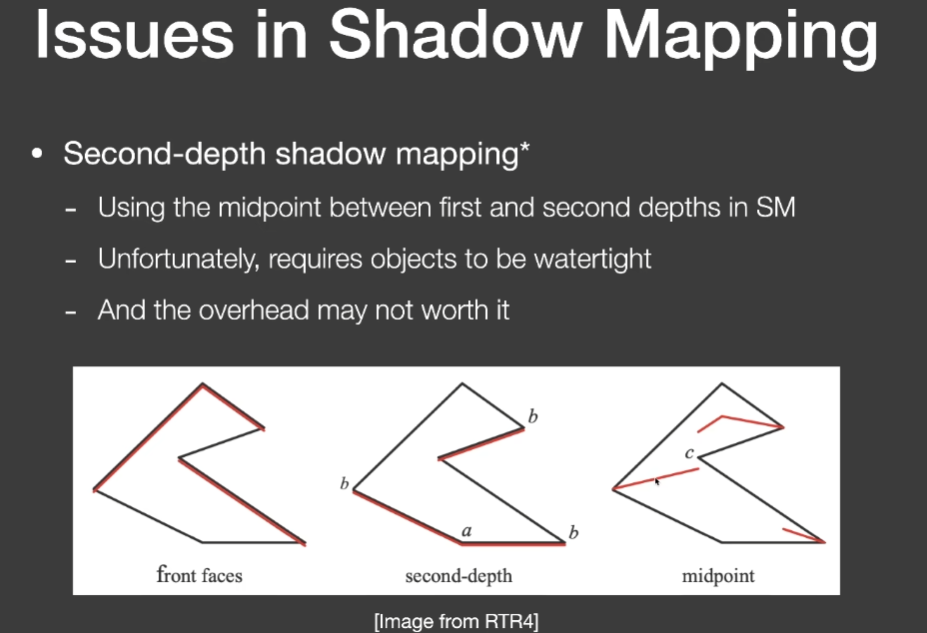
- 一个解决思路
- 实际上没人使用,要求物体是个水密性物体
实时渲染不相信复杂度
The math behind shadow mapping

- 从微积分开始,有很多不等式
- 在RTR中,我们关心的是”近似相等”,更希望把这些不等式拿来当约等式用,特别是建立在一系列条件下

- 一条贯穿RTR不同子领域的约等式
- 想把两个函数乘积积分起来,可以拆出来
- 分母表示归一化常数
- 积分域(support)越小越准确、g(x)足够光滑越准确

- 人们更愿意把visibility项单独拆出来写
- 用刚才的公式可以立刻推导出,把V单独拿出来,右边没有visibility,就是shading
- 对于点光源/方向光源来说,这么拆分是准的
Percentage closer soft shadows (PCSS)
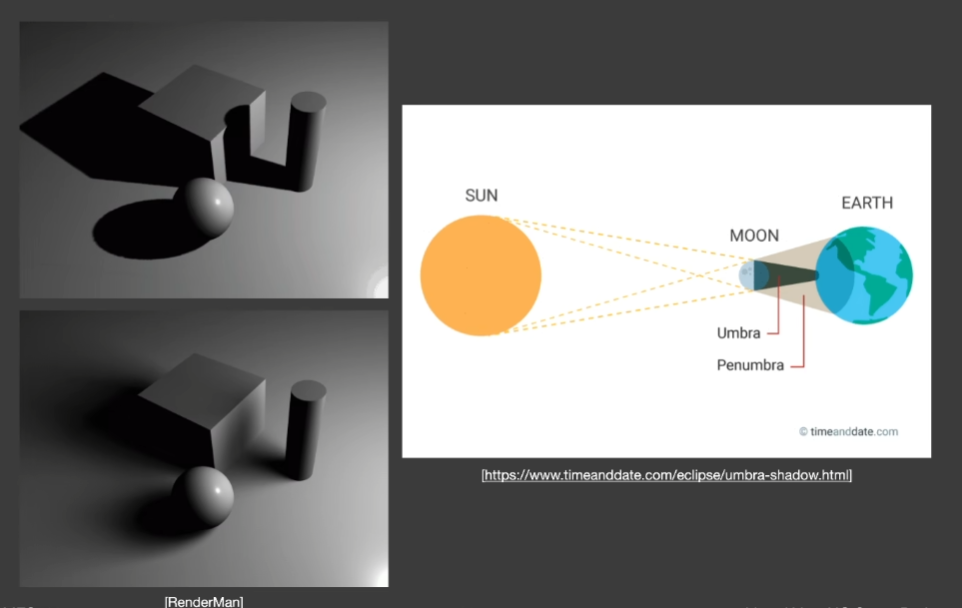
- ShadowMapping产生的是硬阴影,而生活中更多会遇到软阴影
- Percentage Closer Filtering (PCF)是一个工具,最早研发出来用于做抗锯齿,后来人们发现还能被用于做软阴影
- PCF做的是,把任何一个点连向光源看是否在阴影里,是的话标注成0,不是标注成1,对这一系列结果做一个Filtering,实际上是求平均
- 它的Filtering不是指在最后的图上做,不是对ShadowMap进行filter,而是在做阴影判断的时候
- 它平均的是任意一个ShadowPoint做了很多次阴影的比较的结果

- filter区域的大小会决定阴影的软硬
- 所以PCF可以用来做软阴影效果
- 但是要给它多大的filter size呢,是不是各个不同的位置上都要给它相同大小的filter呢。答案是:不是

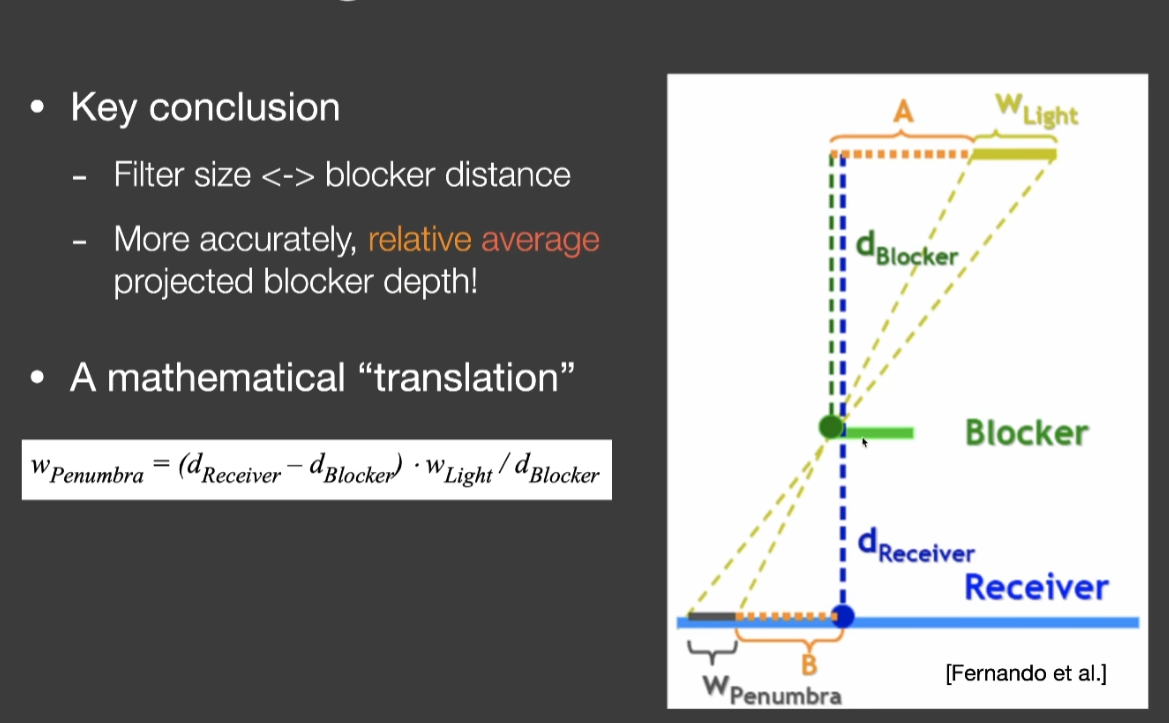
- 人们发现离阴影投射物(遮挡物)近的地方,比较硬,反之较软
- 因此定义一个距离叫做blocker distance
- 准确的说,叫做:相对的、平均的、投射的遮挡物的深度

- 该filter多大,就取决于light的size和blocker的距离
- 对于面光源,无法生成ShadowMap,一般认为它是一个位于面光源中心的点光源
- 而第一步的Blocker search又要取多大的范围呢,一般认为有两种方法
- 取某一固定大小的区域
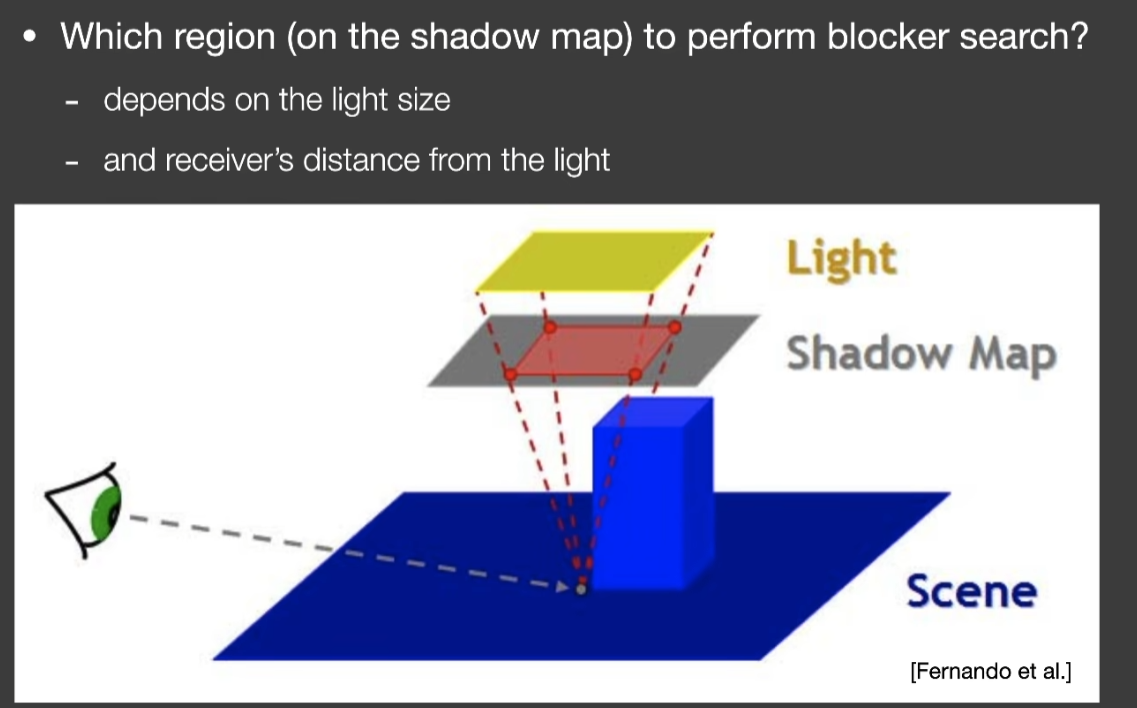
- 另一个更好的方法,对于shading point,想要去找Shadow Map里面的某一块区域在第一步用来做Blocker search,要去红色区域里去估计能挡住shading point的点的平均深度,红色区域取多大,我们认为把light当点光源,放在Light中心,看向物体,认为ShadowMap是在某一位置,比如近平面,就看shading point连向light来看覆盖了ShadowMap多大区域
- 取某一固定大小的区域
- 总结:
- 在任何一个Shading Point,通过上述方式,可以找到在Shadow Map上某一片区域,应该去找哪些像素可能遮挡这个点,这样的像素就被视为Blocker,把它们深度平均起来,如果遇到像素不能遮挡它,就不管它,因为它不是Blocker,记录下Blocker的平均深度后,用公式得到对应阴影应该去fliter多大的信息,之后问题转化成PCF
- 开销是很恐怖的,在做Block search时,要对范围里的纹理进行访问,完成后在PCF里面还得做PCF对该范围的纹理进行访问。工业界给出了一些方法,在下节中说明
- 用PCF去做软阴影,叫做PCSS
Lecture 4 Real-Time Shadows 2
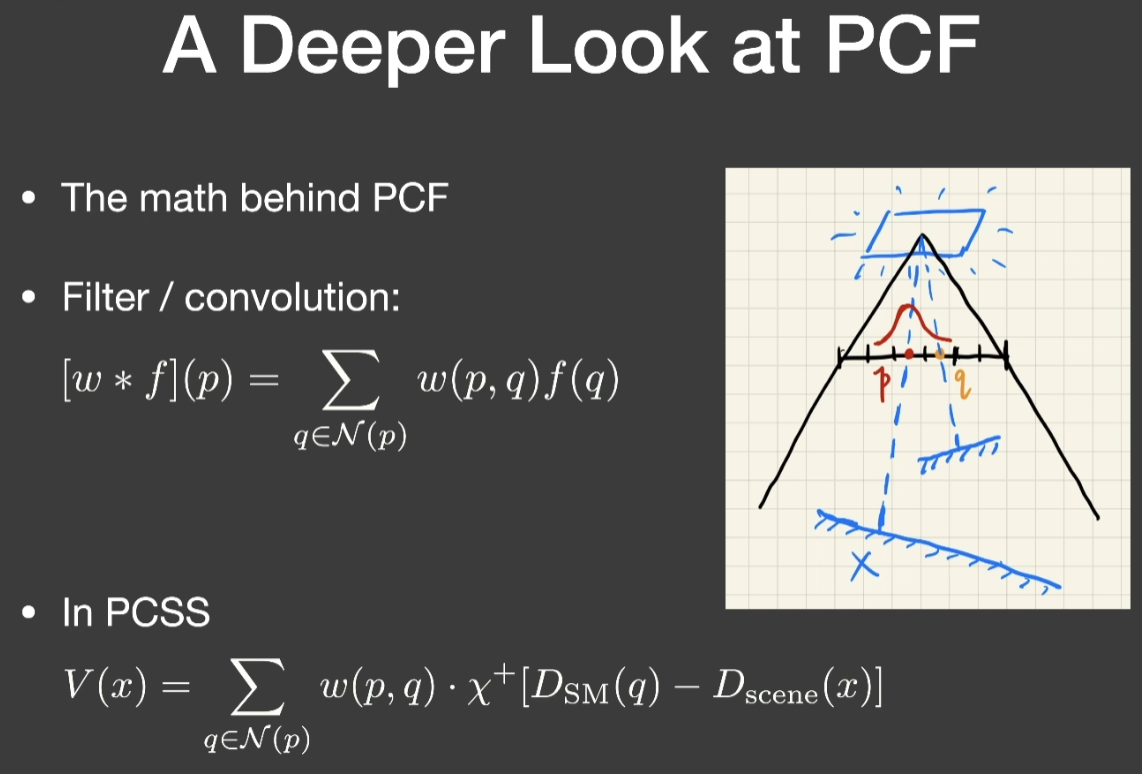
- 实际上做的是,对任意一个像素p,都取周围的一圈领域,邻域中取点q,所有的点q都考虑进来,把所有的点q根据和点p的距离做一个加权,最后重新写回点p
- fliter实际上就是加权平均,convolution(卷积)
- 在PCSS里,做的是点x在Shadow Map上对应点p,附近的任意一个点q是否能遮挡住点x
- 在公式中,只有两项,左边是权;右边是值,阴影比较的结果,点q如果挡到的话visibility是0,挡不到是1。Χ是个符号函数,在微积分里就是个阶梯函数,当它的变量大于0时,Χ的函数值就是1,变量小于0,函数值为0,这正是阴影比较的结果

- 从公式可以看出,它并不是在filter Shadow Map,对SM进行模糊后,最后得到的值还是非0即1
- 也不是在图像上做filter,在一个有锯齿的硬阴影上做模糊,试图去解决抗锯齿的问题,这种做法是在图像空间上来做

- 在第一步和第三步中,都要做在某一区域内,里面所有的纹素和某个深度相比
Variance Soft Shadow Mapping
- 针对PCSS中的第一步和第三步慢的问题
- 从第三步PCF中考虑,在Shadow Map上记录的一块区域内,把里面深度都拿到,看有百分之多少的纹素的深度要比Shading Point要浅
- 而我们不想把每个纹素都看一遍,为了避免这个过程,使用VSSM解决
- 近似的认为是正态分布,只需均值和方差

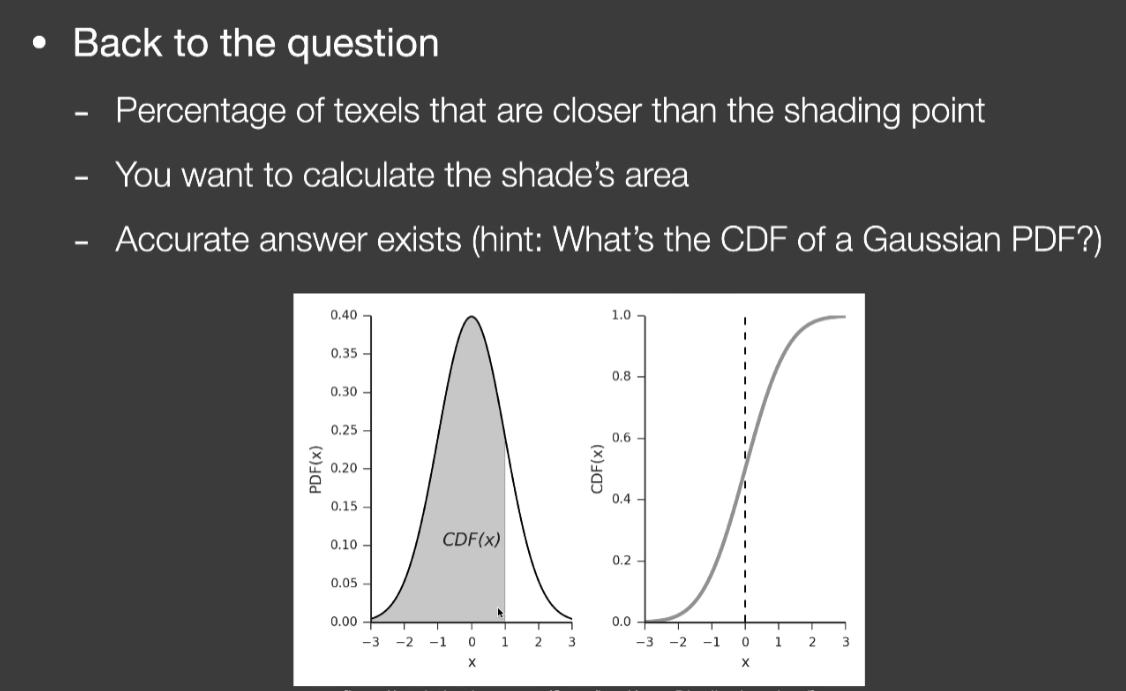

- 切比雪夫不等式,不需要知道是什么分布,只需均值和方差,就能得到近似面积
- 有个限制,t必须在均值的右边
- 用VSSM提升PCSS第三步PCF的fliter质量,需要再生成Depth map的同时,还要生成它平方的map



MIPMAP and Summed-Area Variance Shadow Maps

- 如何对一张图上的任何一块区域快速获取平均值,并且保证这块区域一定是一张矩形

- 最简单的办法是Mipmap,快速的、近似的、方形的范围查询,但不准

- 一个100%准确的方法,引入Summed-Area Table数据结构,跟算法中的前缀和概念紧密结合
- 范围内求平均和范围内求和是同一个概念
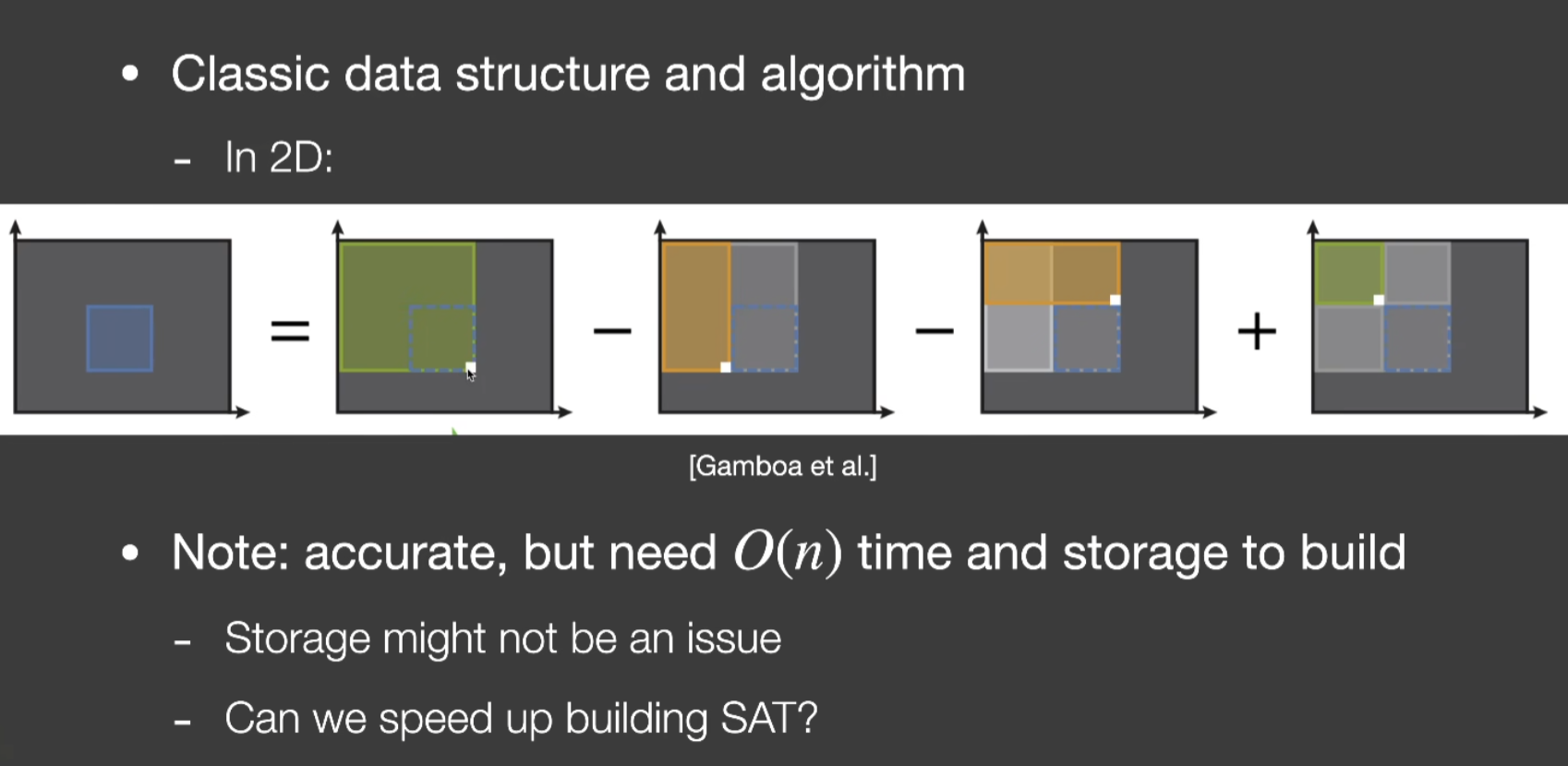
- 二维的情况下
Moment shadow mapping

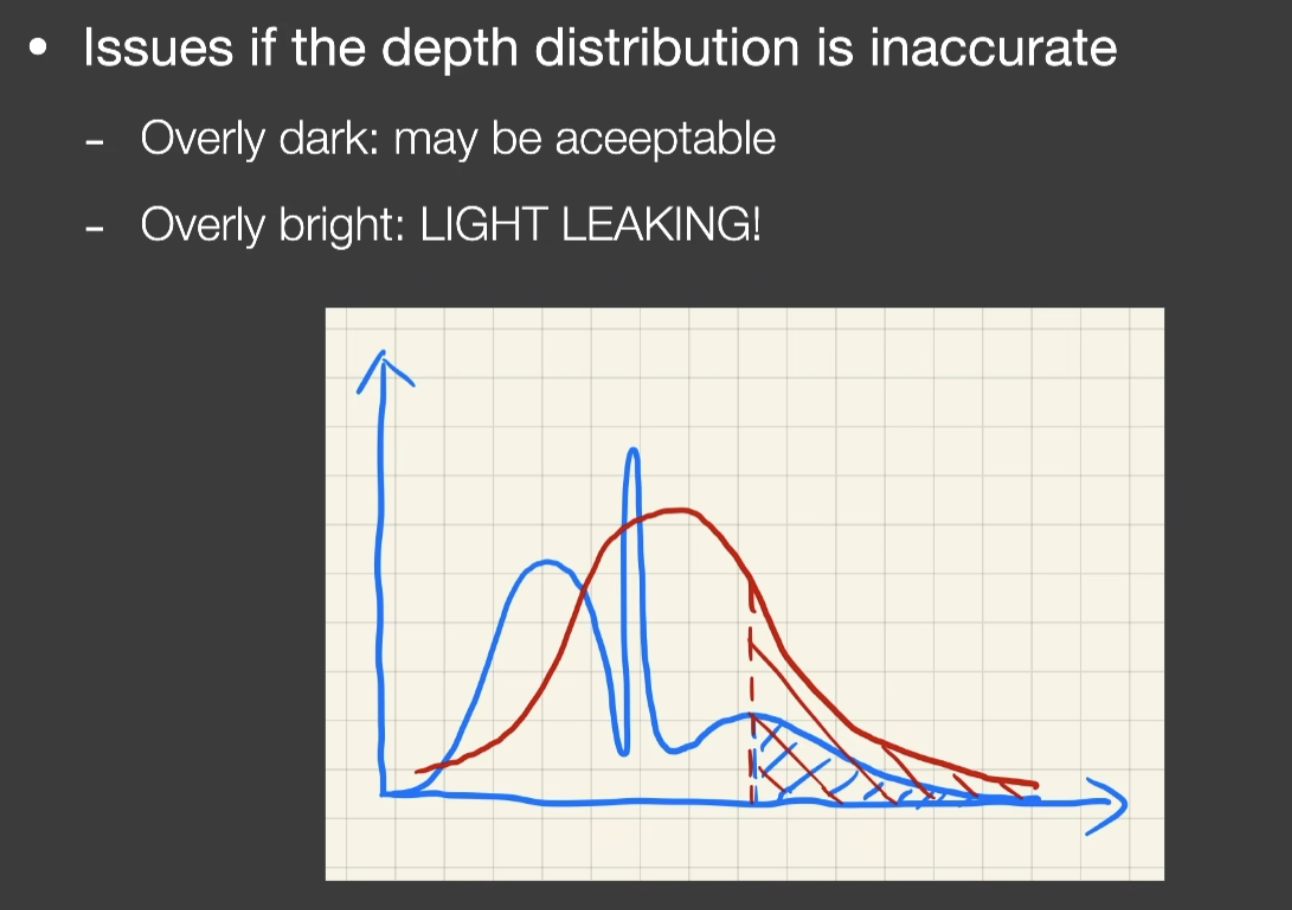

- VSSM的问题体现在它做的假设不正确
- 所以引发一个能不能解决VSSM对分布描述不准的问题
- 做法是使用更高阶的矩(moments),去描述分布
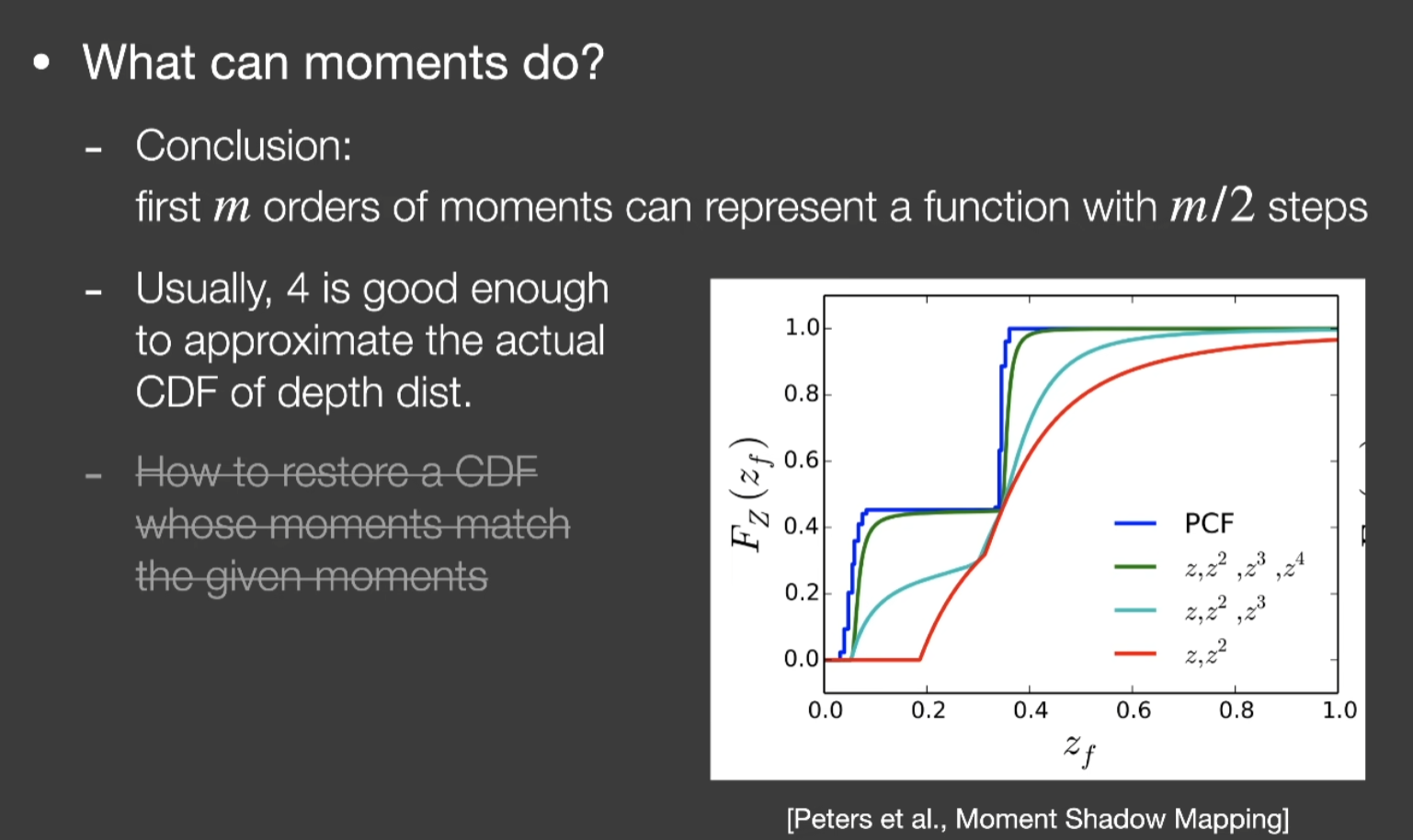

- VSSM用的是前两阶的矩(深度和深度平方),而用更高阶的矩,确实可以获得更接近的分布估计
- 结论:如果保留前m阶的矩,它可以表示一个函数,一个由一系列阶跃函数堆起来的一个函数,并且它能表示m / 2个台阶

- 问题更多的在于对于一个四阶矩,怎么得到有两个台阶的函数,是很复杂的
Lecture 5 Real-Time Environment Mapping
Distance Field Soft Shadow

- 很好的软阴影效果

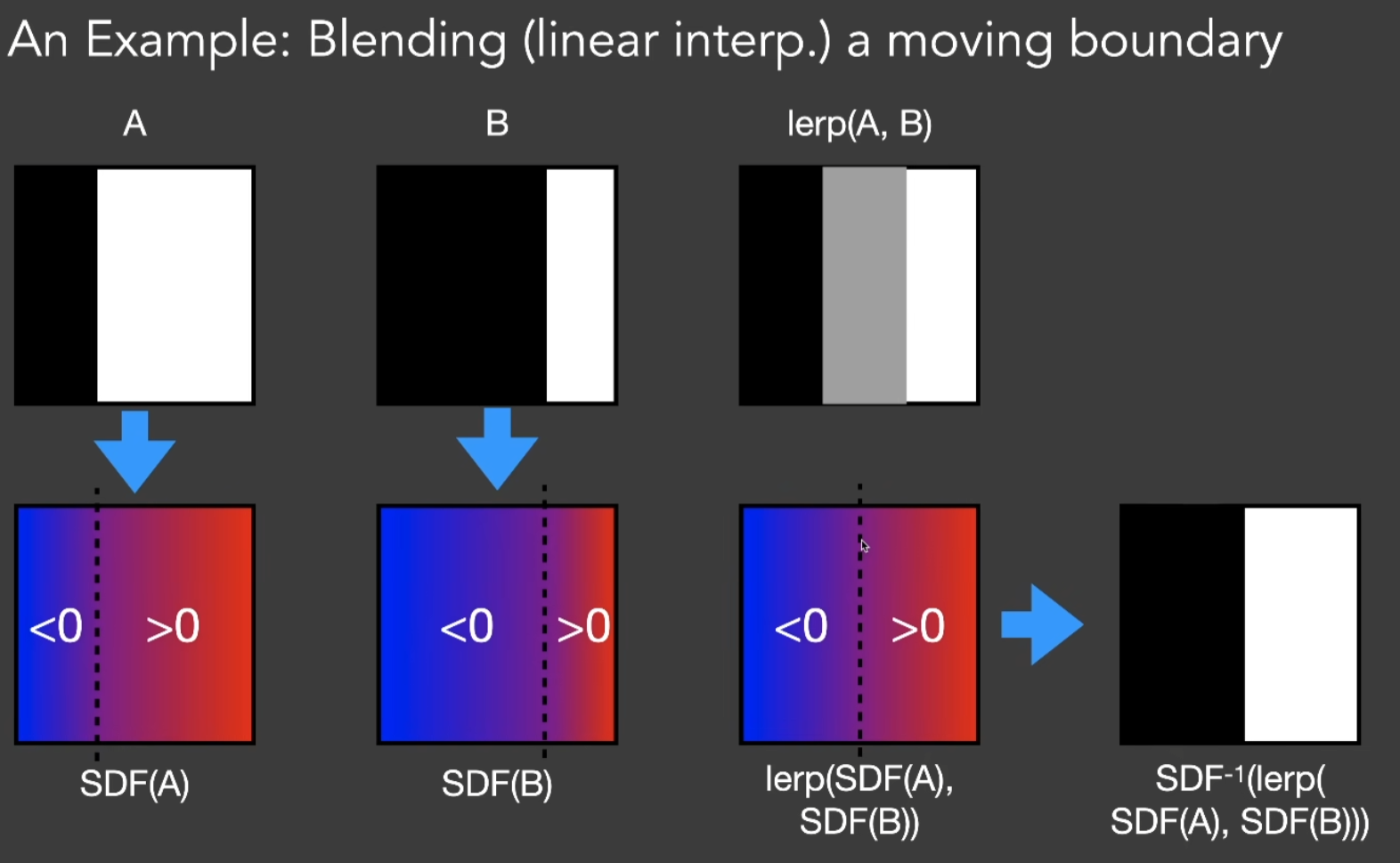

- SDF的背后和一个理论关系密切,叫做最优传输(Optimal Transport)

- 应用1:光线追踪(ray-marching)
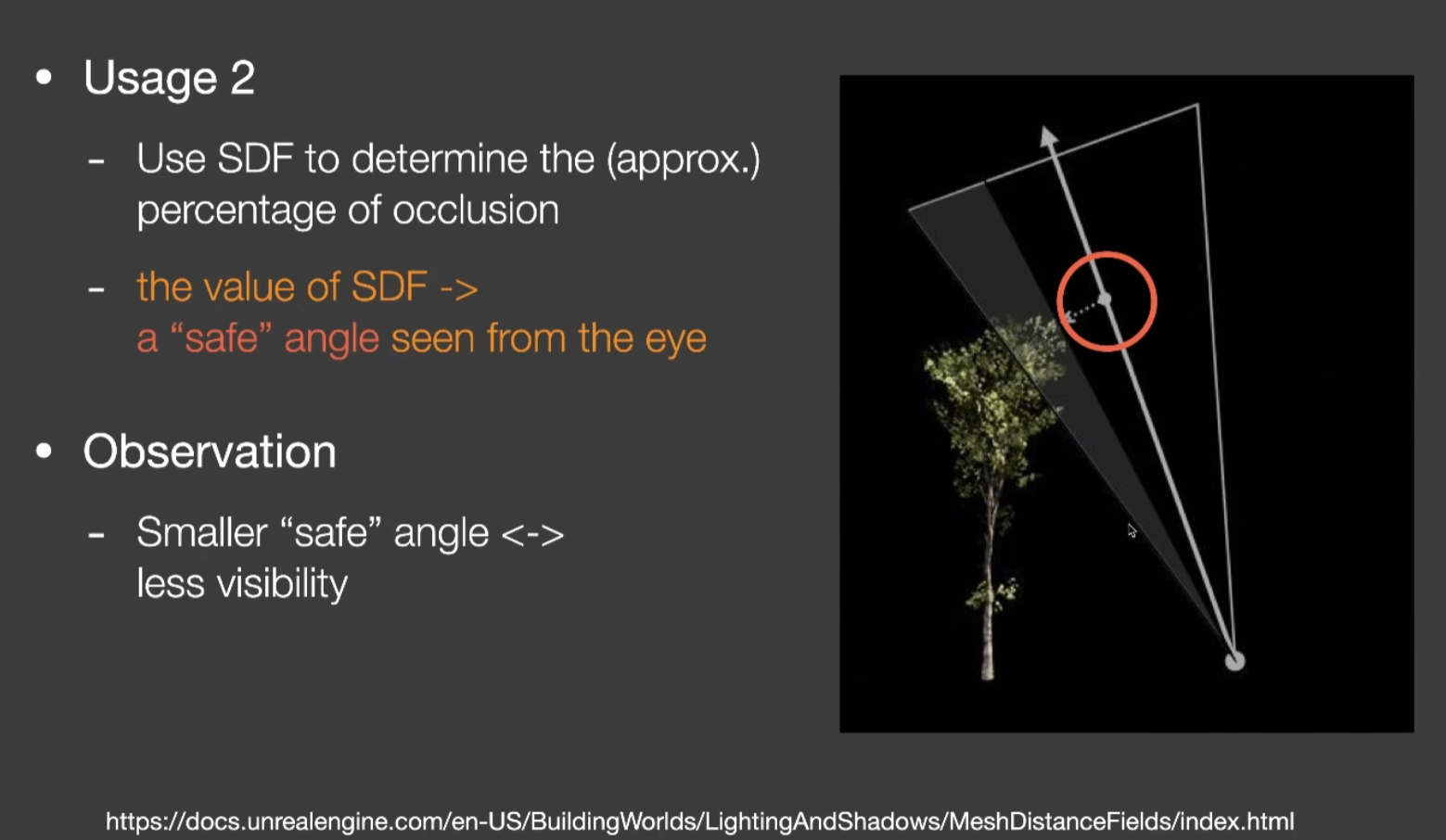
- 应用2:生成软阴影
- 不准,但符合观察
- 将SDF得出的安全距离转化成安全角度,这个角度越小,遮挡越大
- 关心的是如何得到安全角度
- 对每一个安全角度取最小

- 避免复杂的计算,用第二个公式进行近似
- k用于控制阴影的软硬程度。k越大,很小的比值也会得到1,也就是阴影的过渡越小


Shading from environment lighting

- 环境光照:用一张图记录在场景中往任何一个方向看,可以看到的光照
- 认为光照是来自无限远的

- 放一个物体在场景中,在不考虑遮挡/阴影的情况下,如何算出Shading
- 这种操作被称作Image-Based Lighting(IBL)

- 通用的解法就是用蒙特卡罗积分,但对任何一个fragment做会非常慢
- 在shader中使用采样的方法,都不能用于实时渲染(以前这么认为,现在或许有解决办法,也应该避免)
- 在IBL的情况下,任何一点的Shading不通过采样来得到
- 基本思路从观察开始
- 在rendering equation里面,不考虑visibility,是两个函数相乘再积分,一个是Lighting,一个是BRDF项
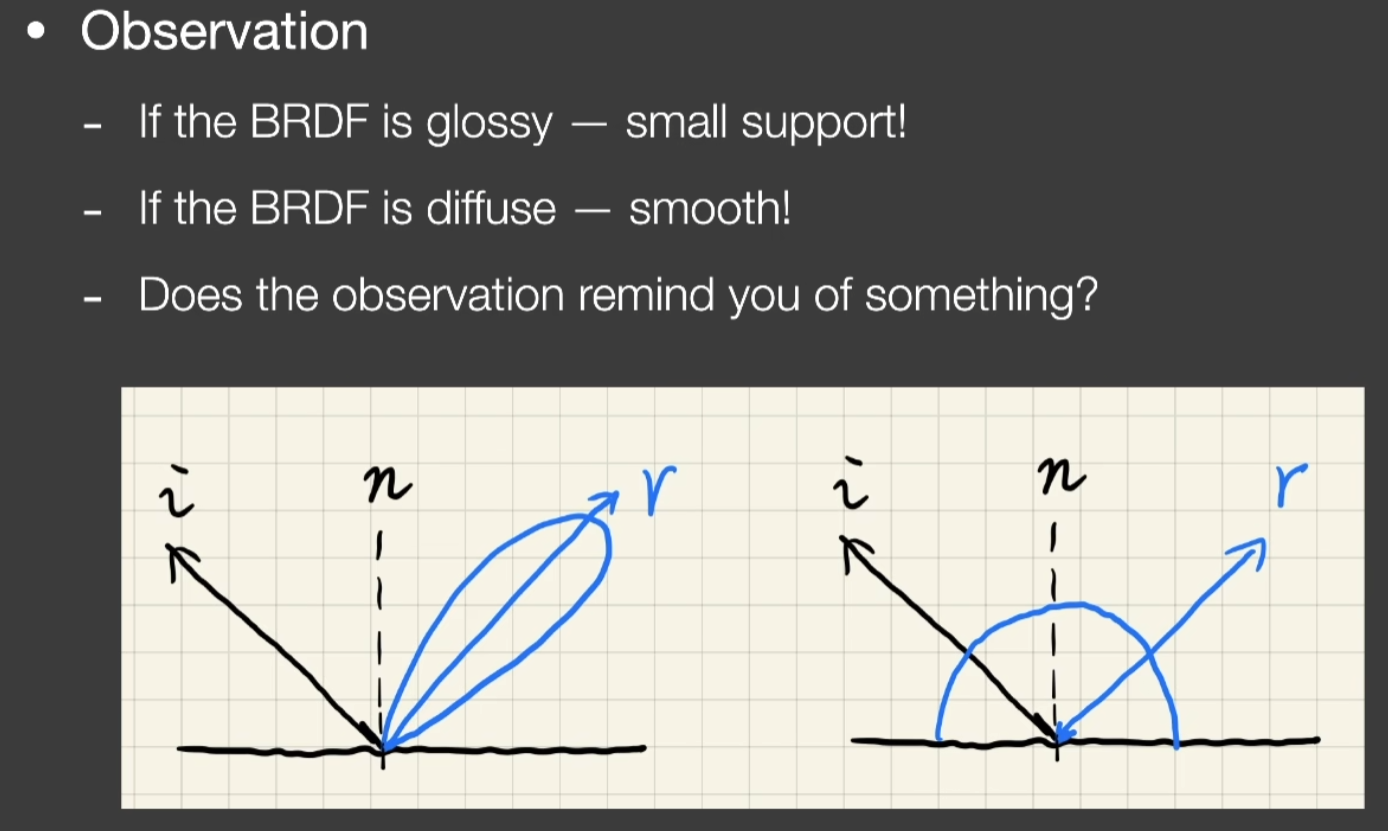
- 观察是这样的:如果BRDF是一个glossy的BRDF,渲染一幅图,从视角Incident,它覆盖的球面是很小的;如果是diffuse的BRDF,从入射方向看过来会向四面八方反射,在球面上会覆盖整个半球的区域,虽然区域非常大,但是非常smooth,它的值变化不大
- 如果BRDF是glossy的情况,它support就小;如果BRDF是diffuse,它就smooth

- 之前(Lecture 3)的近似方案
- 这里显示的把support写出来
- 在g(x)support比较小,或者g的值比较smooth的情况下,这个近似较为准确,对于BRDF来说,非常满足这个性质

- 所以可以做一个拆分,把除了BRDF(类比于g(x))以外的另外一项f(x)拆出来,对应这里的光照
- 光照在BRDF范围内的积分,去除以BRDF范围内的空的积分,做归一化
- 区分于做阴影时,把光照和BRDF留在里面,把visibility项拆出来,这个公式是可以根据需要来选用的
- 正是因为light和BRDF综合考虑挺难的,把light拆出来,发现就是在light所表示的球上,BRDF的lobe所覆盖的区域,把这个区域的light积分起来并且normalize
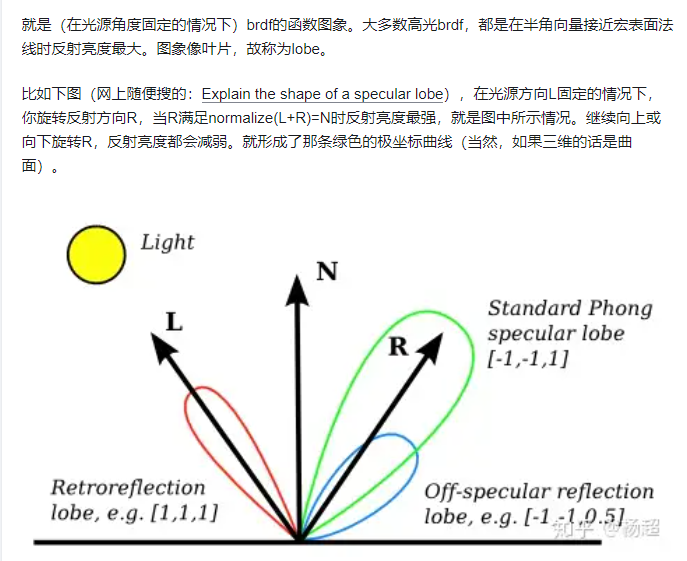

- 所说的事就是把IBL表示的图给模糊了
- 做拆分能够让lighting做一个pre-filter
- 做pre-filter能干什么:
- 左边不用做采样的部分拆出来后,还需要计算右边剩下的部分,是一个BRDF的积分
- 可以做一个预结算,这里的预计算比较麻烦,因为要把所有的参数考虑进去

- 如果想预计算一个积分的值,它的参数空间非常高维,需要想办法降维
- 人们法线菲涅尔项用Schlick这种近似方式可以写成一种形式

- 把R0提出来,也就是消除了对基础反射率的依赖,剩下来只有两个变量,BRDF的Roughness和入射角θi
- 这时想做预计算只需对两个变量打一个表

- 人们法线菲涅尔项用Schlick这种近似方式可以写成一种形式

- 通过以上两部分的处理,可以做到不需要采样,还可以在环境光下渲染不同的物体,得到一个非常好的结果

- 把一个积分或求和拆开,对两边再分别进行filter或查表,分别求和,这种方式本身有个名字,叫做split sum
- split sum就是UE引擎PBR做到那么好的基础
Lecture 6 Real-Time Environment Mapping

Shadow from Environment Lighting
- 不幸的是,非常难做
- 两个思路:
- As a many-light problem:
- 把环境光理解成多个光源,每个光源需要生成一张Shadow Map,消耗线性于光源数量
- As a sampling problem:
- 当成采样问题,每个Shading Point去解Rendering Equation,其中Visibility项是最复杂的问题;如果做Visibility项的拆分,要求support越小越准确、g(x)越光滑越准确,而Glossy的BRDF是高频的,环境光L这项的support是整个半球,所以不太容易做
- As a many-light problem:

- 工业界在用的方法:
- 在环境光中取一个最具代表性的光源,比如太阳,从这个最亮的光源生成一张阴影
Backgroung knowledge
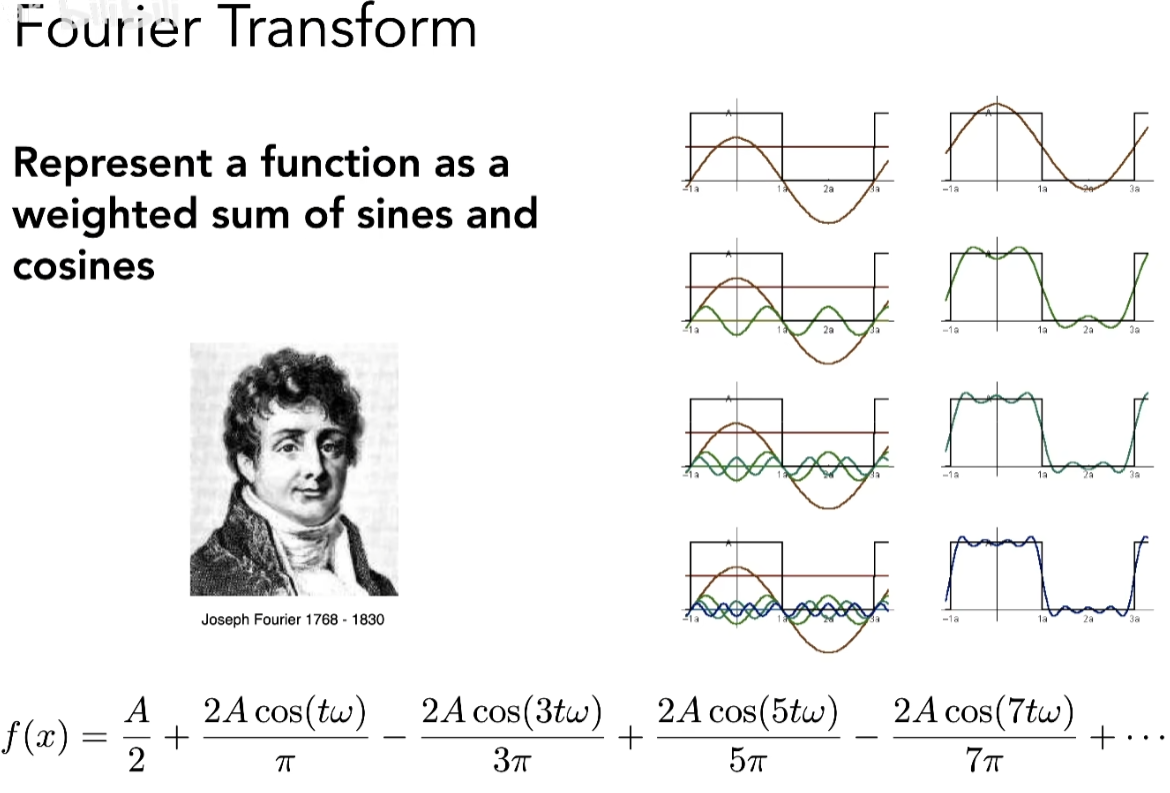
- 傅里叶级数变换
- 任何一个函数都写成一堆sin和cos的线性组合,并且这些函数都有各自对应的频率,这些函数称为基函数,这些基函数前面乘上系数再加起来,就能得到原始函数

- 一般讲频率的高频还是低频,就是指变化得快还是慢,不是时间层面的变化,而是在空间上,颜色变化得剧烈不剧烈

- 滤波(Filtering)是指去掉一系列对应频率上的内容
- 低通滤波器,留的是比它低频的频率
- 对于一张图,只保留低频的部分,还是基本能看清的
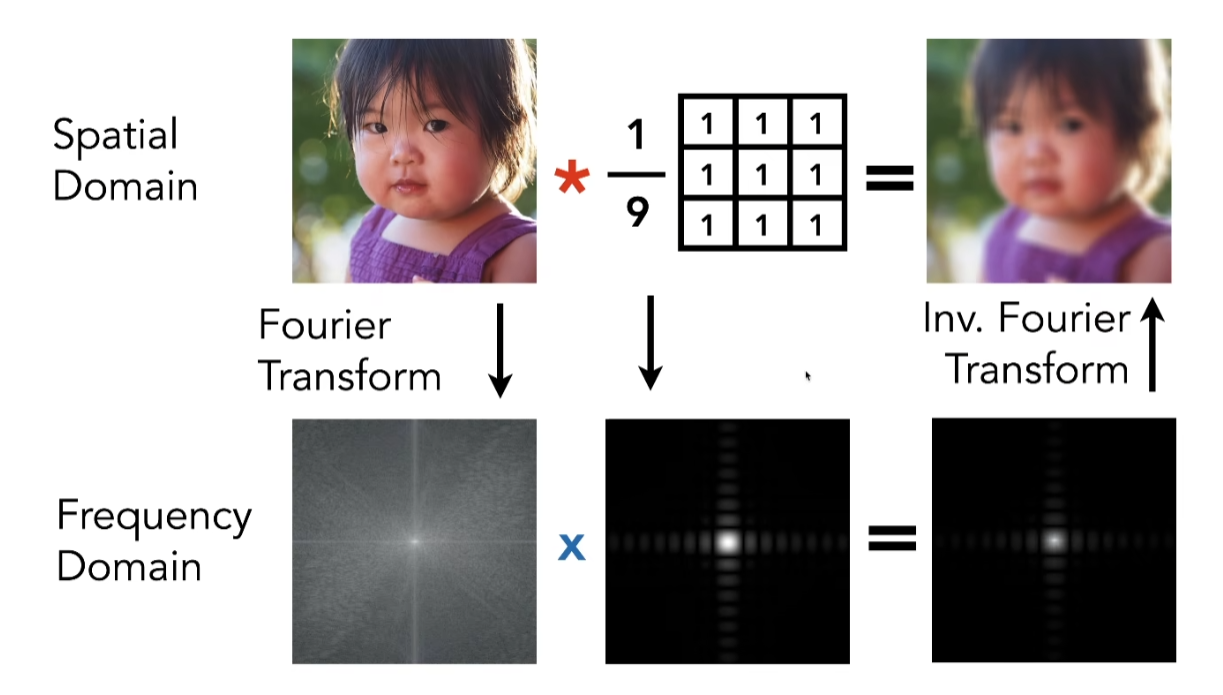
- 实域做卷积,相当于在频域做乘积
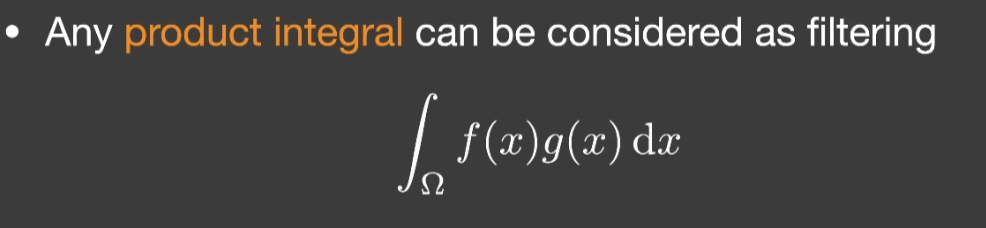
- 认为两个函数乘积再积分起来就是一个卷积/滤波操作
- 可以理解成实域上的两个信号卷积,等于频域上两个信号相乘
- 频域上两个信号各自的频谱,其中有一个是低频的,它们在频域上相乘的结果就是低频的,再积分的结果也是低频的
- 只要满足上述式子的性质,叫做product integral,认为存在一定的滤波意义


Real-time environment lighting
- 先不考虑Shadow,在都是diffuse物体的情况下做Shading
Spherical Harmonics
- 球面谐波函数
- 它是一系列二维的基函数,并且都是定义在球面上的
- 非常像一维的傅里叶级数
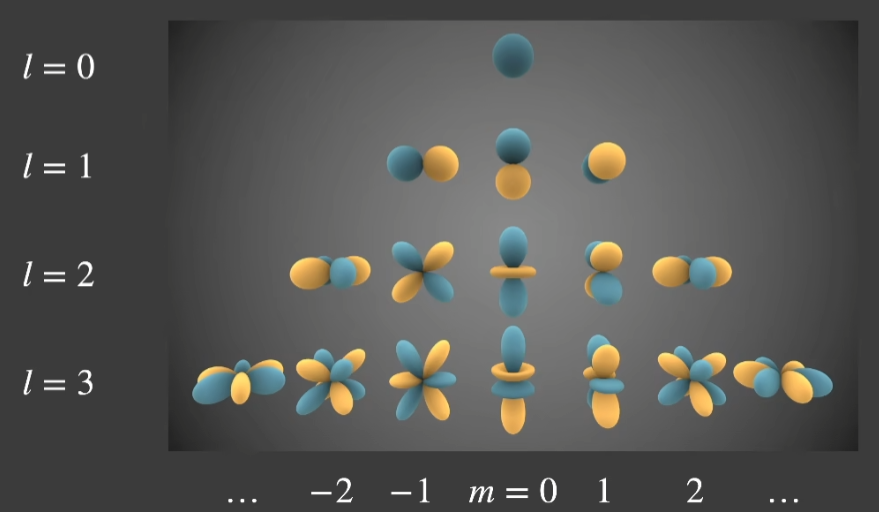
- 不同频率的函数个数也不同
- 每阶(l)的SH有2l + 1个不同的基函数,并且它们有固定的编号
- 前n阶有n^2个基函数
- 阶越高,对应的频率越高,基函数的数量也越多
- 每一个基函数利用勒让德多项式来写
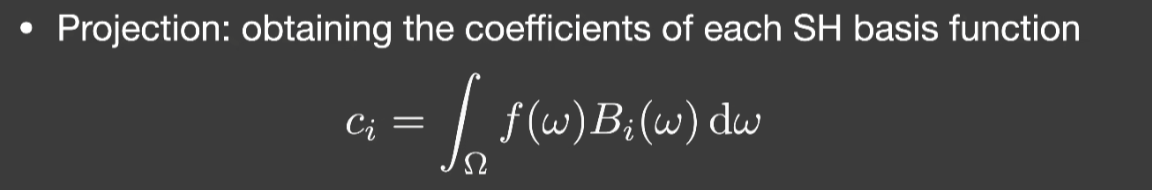
- 任何一个二维的球面函数,如果展开成用SH的线性组合来描述,对于任意一个SH,Bi(x),前面的系数ci,可以用这条性质来得到
- 对应位置逐点相乘再积分
- 用基函数来描述的时候,求任何一个基函数的系数ci的过程称做投影,任何一个函数f(ω),都可以求出它在任何一个基函数上的投影
- 如果想用基函数来恢复出原来的函数,人们并不想用太多阶去表示,如果只用前四阶来表述,已经可以得到不错的结果,恢复出的函数只保留了最高阶的频率
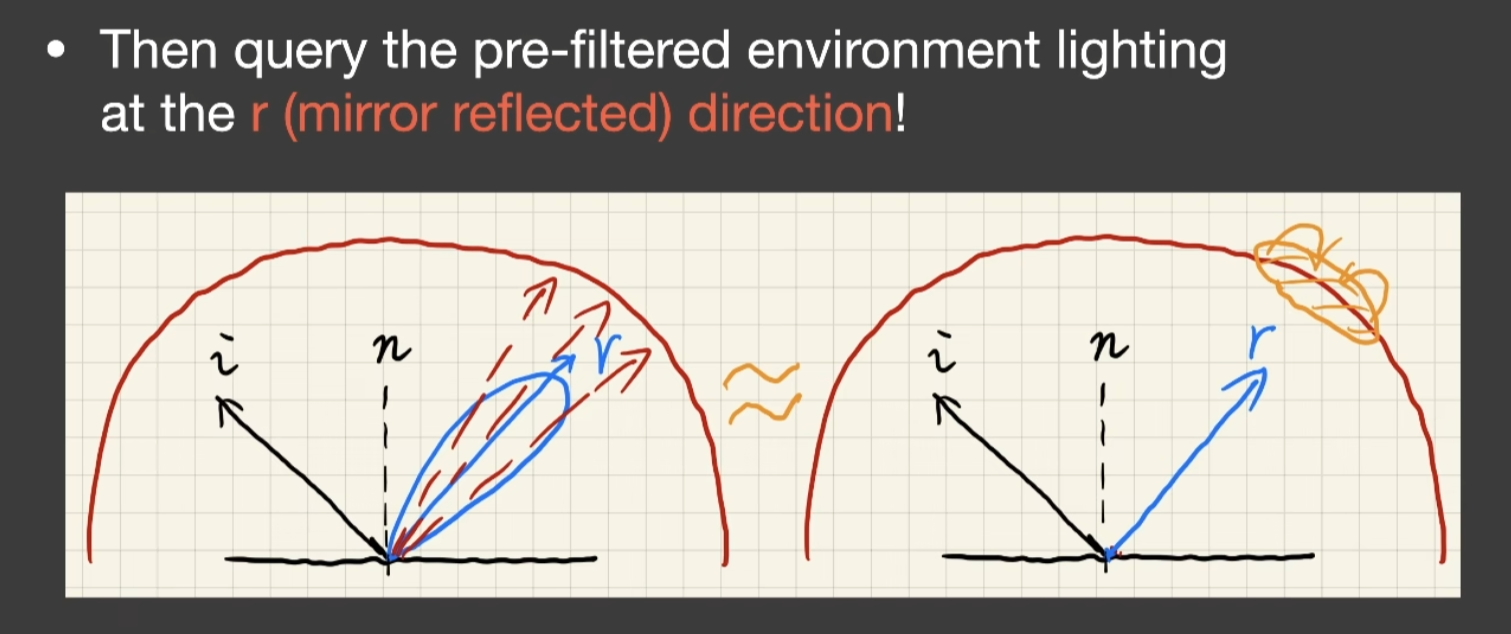
Recall: Prefiltering

- 如果有一个环境光,沿着镜面反射方向去查它的某一个值,会感觉在看一个镜子
- 如果先把环境光做一个filtering,也就是模糊,同样去沿着镜面反射方向查它的某一个值,看上去就是diffuse
- 所以Prefiltering过的环境光加上一次查询,就好像不做任何的滤波,在任何一个点去查任何一个方向的环境光它的值是多少,这两个基本等价
Diffuse Shading in Render Equation
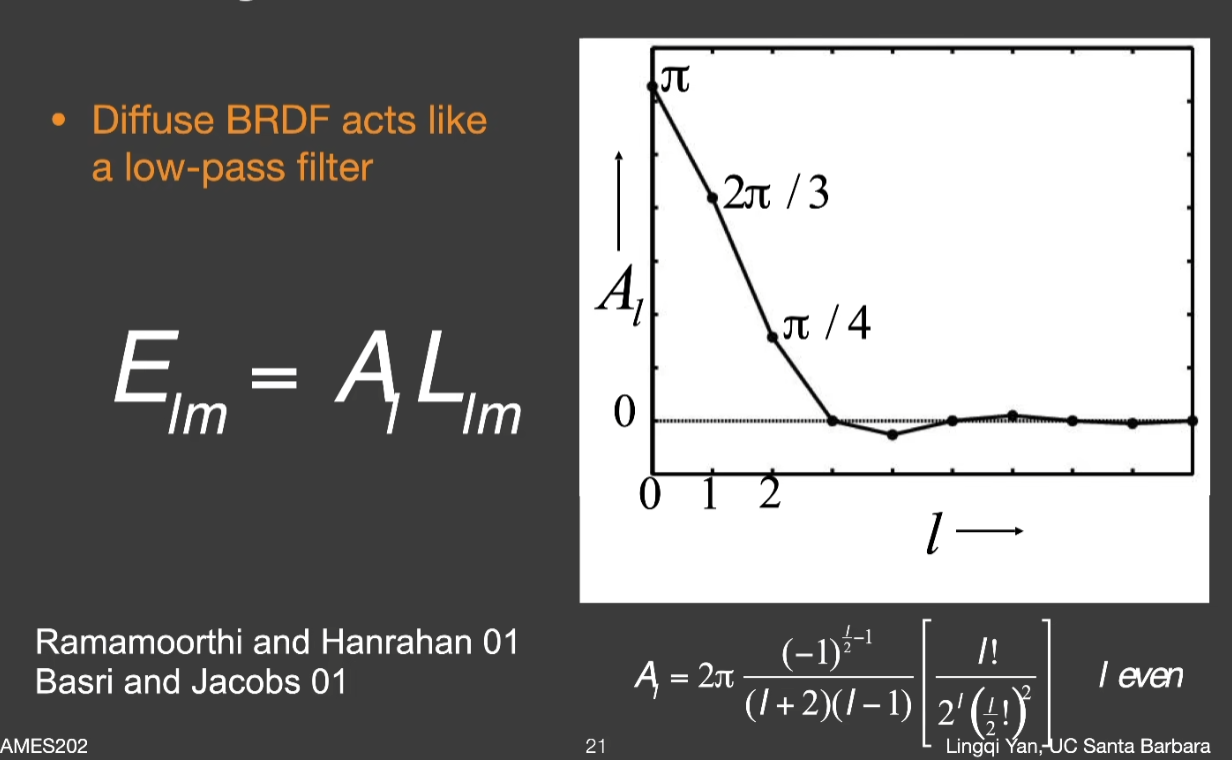
- Diffuse BRDF之所以简单,因为Diffuse是Smooth的
- 在Rendering Equation里,我们要解决的是Lighting乘以BRDF,只考虑Shading,没有Visibility项
- Lighting是整个Environment map过来的一个球面函数,整个BRDF是定义在半球上面的很光滑的函数,它们两个做逐点的相乘然后积分起来,正是product integral的操作
- 环境光可能很复杂,有高频有低频,而BRDF在Diffuse时有个很好的性质,好像是一个低通滤波器
- 所以,是否可以用很少的SH基函数来描述Diffuse的BRDF,实际上用三阶就可以很好地描述
- 可以理解为,要把Diffuse BRDF投影到SH,只有前面几阶有值,意味着它根本就没有后面几阶描述的高频信息
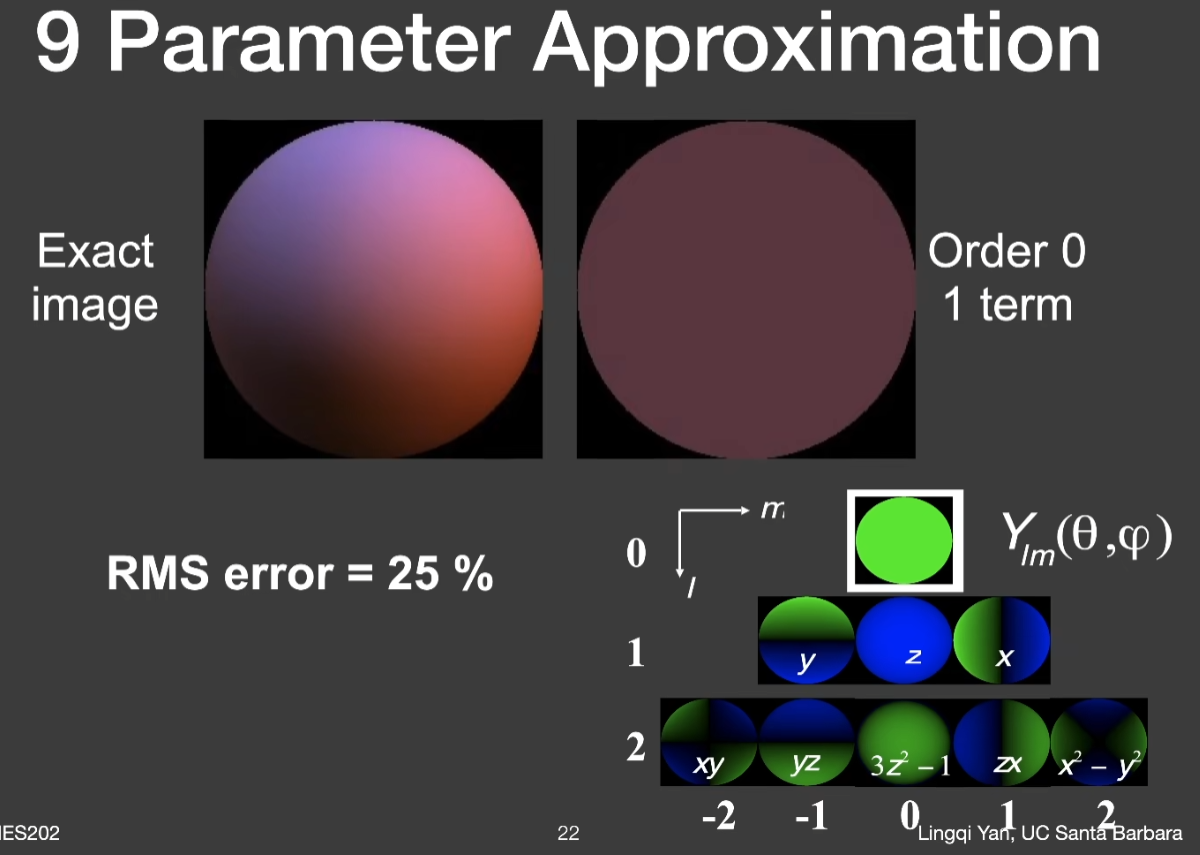
- 由于两个函数做product integral时,两个函数乘出来的结果的频率肯定由较低频率的函数决定。因此环境光不管有多高频,只要用它照亮一个Diffuse物体,基本看不到什么高频信息
- 显而易见的是,diffuse球上不会反射出多复杂的光照
- 既然BRDF可以用非常低频的前三阶SH来描述,那为什么Lighting要用那么高的频率呢

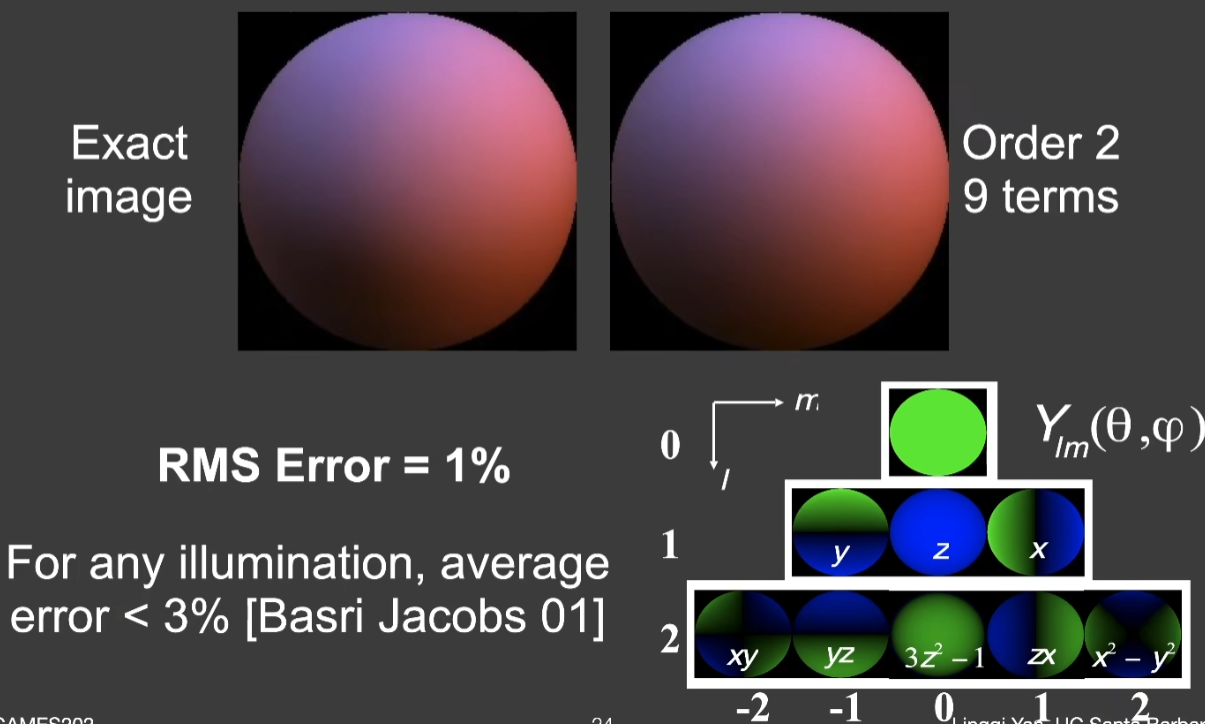
结论:对于任何的光照条件,只要材质是Diffuse的,都可以用前三阶的SH来描述光照,用它照亮Diffuse的物体
剩下的问题:
- 没有阴影
- 其他材质

PRT


- PRT的思想认为,整个场景其他东西都不变,只有光照可以发生变化
- 把Rendering Equation里面看成两部分
- 把Lighting表述成一系列基函数乘系数再相加

- Diffuse下计算Shadow + Shading
- 代价是场景中的物体都不能动
- 对于预计算的光源,如果把它投影到SH上,如果光源发生了旋转,可以立刻得到旋转之后SH前面的系数如何变换
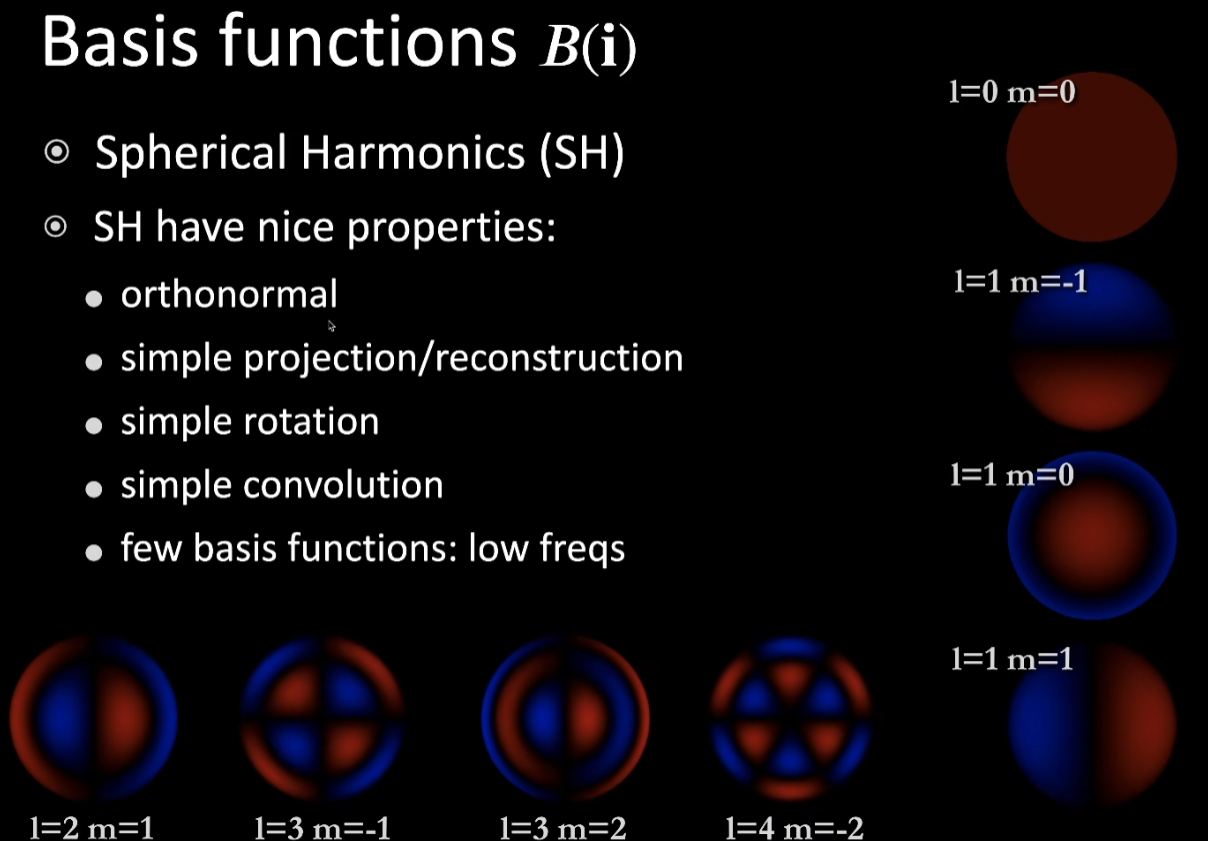
- SH有一些很好的性质
- 正交性:SH是一组正交基。把一个基函数投影到任意的另外一个基函数上去,会得到0(投影到自己是1)
- 非常支持旋转,任何一个旋转后的基函数,都可以被同阶的基函数的线性组合得到

Lecture 7 Real-Time Global Illumination (in 3D)


Diffuse Case

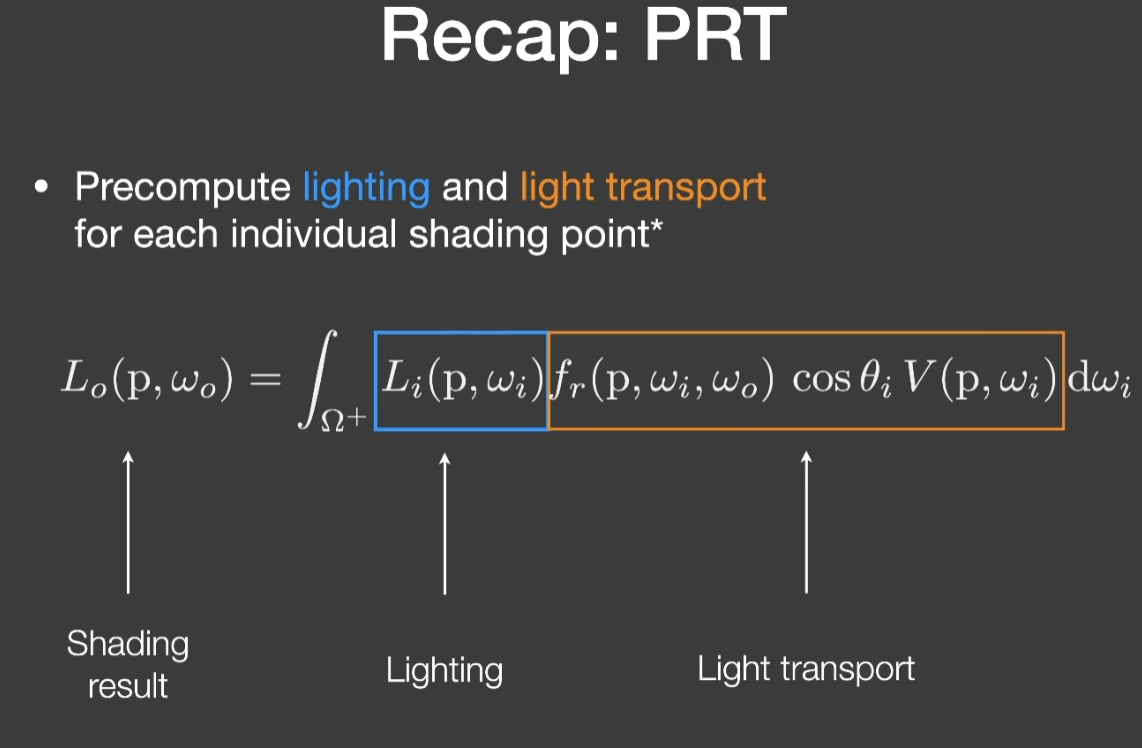
- 对于lighting和light transport如何做预计算
- 上节中从Rendering Equation出发,先把lighting写成一个加数的描述方法,剩下的部分就好像把light transport投影到basic function上。这是一种理解
- 另外一种理解是不考虑先后顺序,两部分分别做

- 变成一个双重求和的问题
- 由于基函数的正交性,只有p和q是相同的基函数时,右边的结果才是1,否则为0
Glossy Case
- Glossy与Diffuse区别在于BRDF,Diffuse的BRDF是一个常数,而Glossy的不是,是四维的函数(两维输入,两维输出,用phi和theta定义一个角)
- Glossy的物体是和视角有关的,给一个不同的视角就会有不同的结果
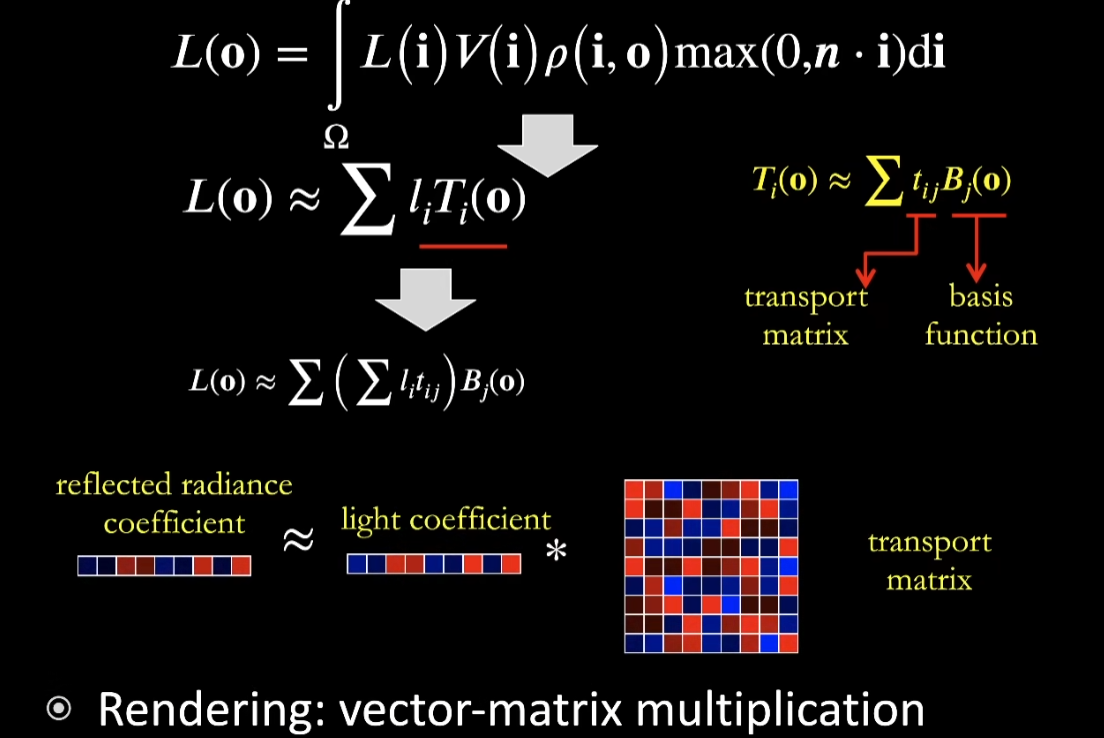
- 既然已经将四维的light transport投影到一个二维的东西上去了,剩下来系数Ti虽然是o的函数,但也只是o的函数了
- 既然是二维的o的函数,可以在o的方向上投影到SH上去,就能得到light transport这里不再是一个向量了,而是一个矩阵


- 为什么说可以把多次反射当成light transport的一部分

- 一些更高阶的算法中,可以对不同的路径分类,可以用一系列的表达式来描述一系列的路径都是什么类型
- 比如光线从发出就直接被看到,可以写成LE(Light Eye)
- 正常情况下区分材质,特别是在实时渲染里面,一般分为三种:Diffuse、Specular、Glossy
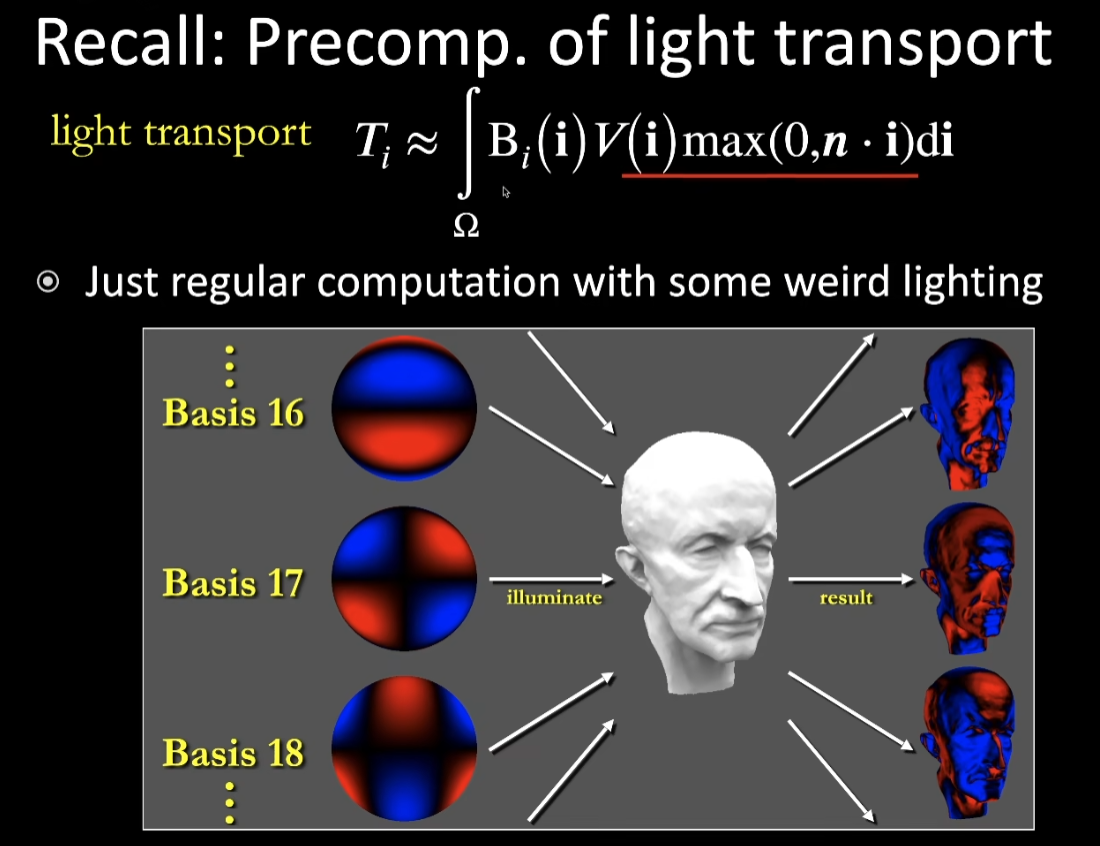
- 对于任意复杂的light transport都可以认为等于是给定了一个光照,整个光照就是SH的基函数,用它渲染出来的结果

- 总结之前最早的这篇PRT
- 提出了用SH的基函数来描述lighting和light transport两部分
- 对于Diffuse的情况下,可以在实际的渲染过程中每个顶点做一个点乘的操作
- 对于Glossy的情况下,每个顶点做一个向量乘以矩阵的操作

- 它有它的问题
- SH基本上只适合用于描述低频的函数
- 由于是预计算,要求场景是静态的、材质是静态的(BRDF是预计算的,不能改变)

Wavelet
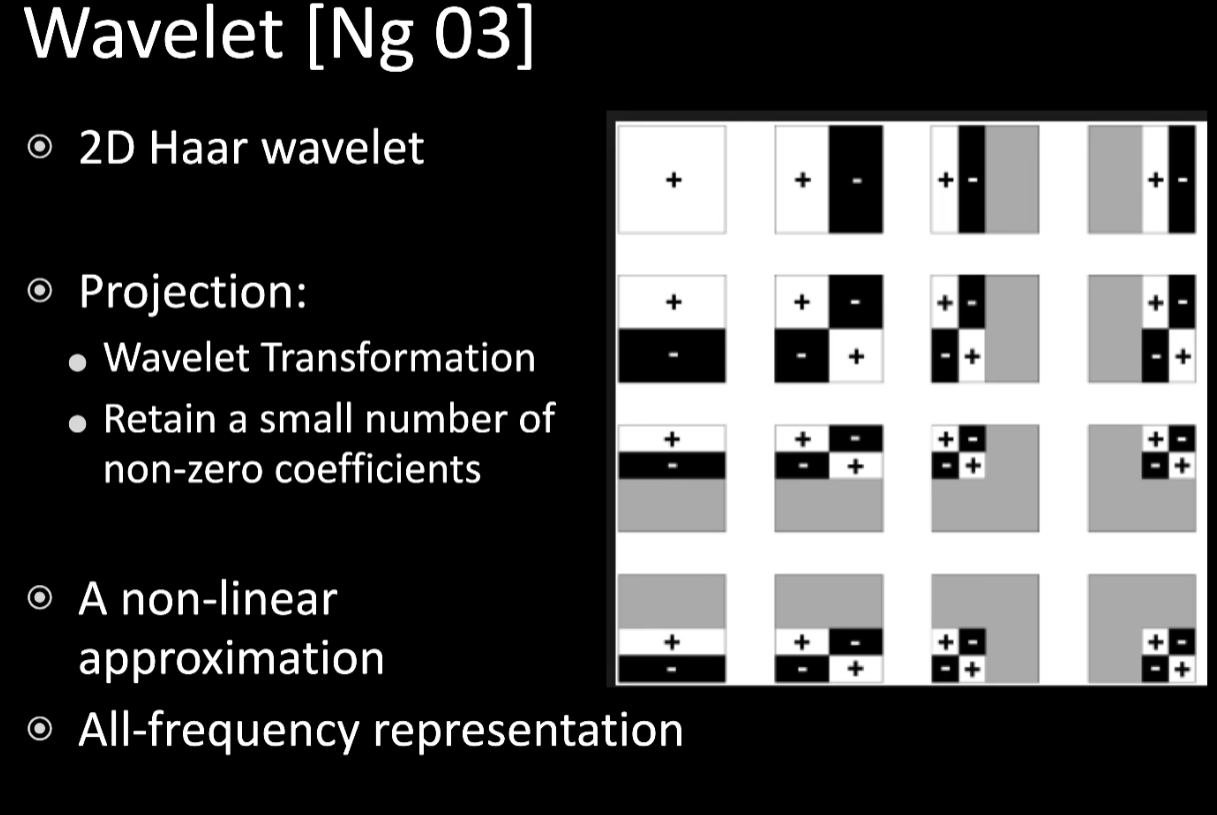
小波函数
定义在图像块上
压缩方式:
- 对于任何一个2D的函数,可以投影到任何一个小波的基函数上去,会发现大量的时候是这种情况,很多基函数对应的系数是接近0的
- 压缩思路就是取对应系数最大的几个,接近0的都不要了
- 这种保留非0或取最大的几个来近似地描述或恢复原始函数,和SH相比,有个最大的好处是支持全频率的表示
怎么样把任何一个函数投影到小波上去,如何用它描述球面上的函数
- 用CubeMap



- 每张图单独做小波变换,把每一张图投影成小波的系数
- 对于任何一张图,它都把高频信息留在右上、右下、左下三个小块里面,稍微低频的东西集中在左上
- 左上还可以继续做小波变换,可以发现绝大部分地方是0
- 不断去做小波变换,可以得到不错的结果
- JPEG的格式用了类似于小波变换的变化:离散余弦变换(DCT Discrete cosine transform)。
- 通过先投影,再取非0的投影出来的系数,得到非常强烈的压缩
- 小波不支持快速旋转
Real-Time Global Illumination (in 3D)

- 全局光照 = 直接光照 + 间接光照
- 实际上人们解决的就是比直接光照多一次bounce的间接光照,人们希望实现起来简单、快速
- 想要得到p点间接光照的结果(用次级光照得到的Shading)需要什么?
- 1.哪些是次级光源/哪些点会被直接光照照到 => Shadow Map
- 2.它们各自的贡献是多少
- 如果需要用次级光源(Shadow Map上的每个像素)去照亮点p,观察方向相当于从点p去观察这些次级光源,所以出射方向是未知的,无法计算Shading
- 因此,为了不依赖出射方向,假设所有的反射物(Reflector)都是Diffuse,不需要假设接收物(点p)也是Diffuse的
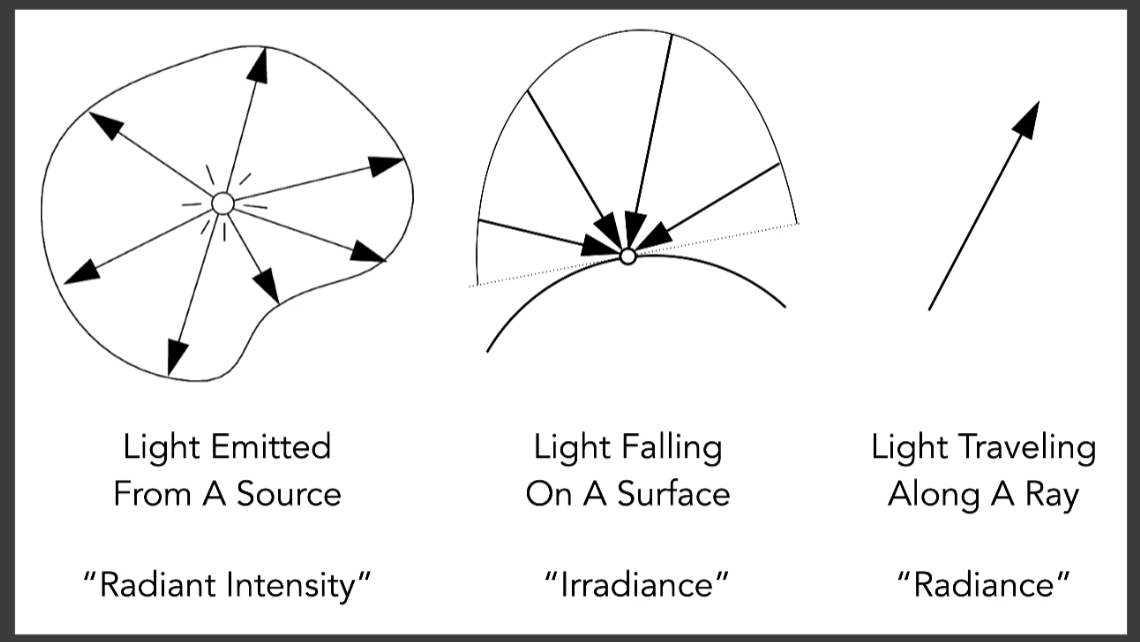
- 回顾辐射度量学
- Flex/Power : 表示能量是多少
- Radiant Intensity : 一个单位立体角上对应的能量是多少
- Irradiance : 单位面积对应的能量
- Radiance : 单位面积、单位立体角上对应的能量
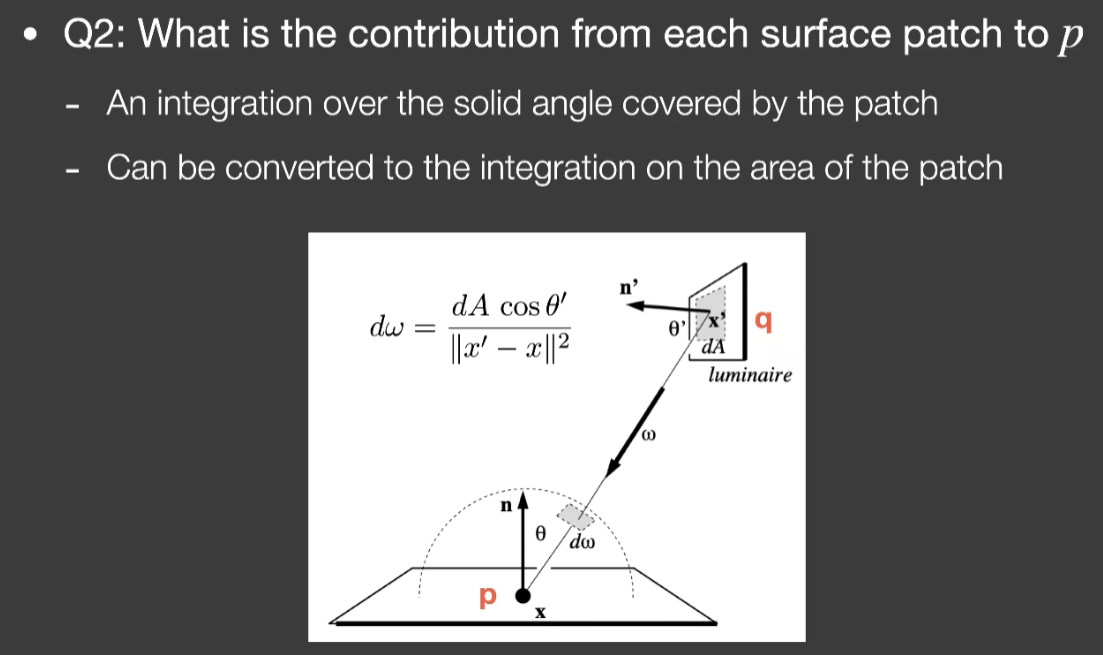
- 先考虑一个patch,最后把所有的加起来
- 避免浪费,在light上采样

- 用变量替换的方式把立体角描述成对Area的积分
- 对于一个Diffuse的reflective patch,BRDF是一个常数
- 出射的Radiance如何跟BRDF联系起来
- BRDF定义:出射的Radiance除以入射的Irradiance
- Irradiance定等于Flex除以这块面积
- 当把Li如此描述后代入,会发现Area都被消掉了
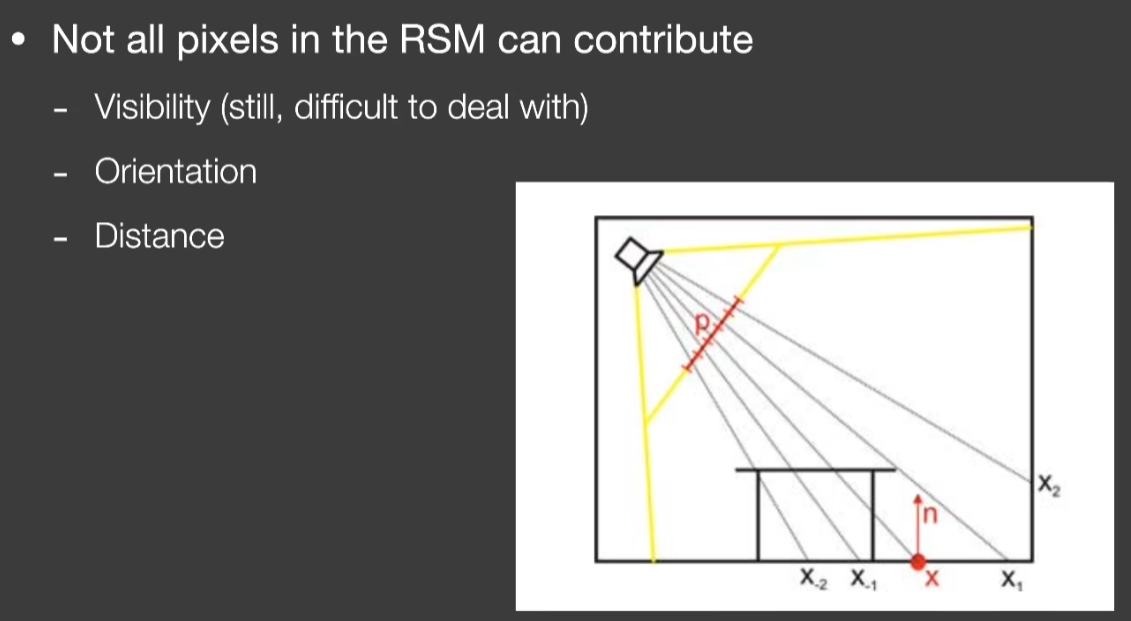

- 距离如果离得非常远,它的贡献非常少,,所以对于一个Shading Point,只需要找离它足够近的次级光源就行了
- 这个观察引出了一个猜想:在世界坐标下两个点比较接近,不好找,那么就把Shading Point投影到Shadow Map上,在Shadow Map上周围的一圈找深度比较近的点


- 特别适用于手电筒

- 优点:非常好写,其实就是Shadow Map的流程
- 缺点:
- Shadow Map本身的问题,有多少个直接光源就得做多少个Shadow Map
- 计算过程中不去算Shading Point到反射物之间的可见性,会造成不真实的情况
- 做了很多假设,都会对质量造成影响
- 采样越多越好,tradeoff
Lecture 8 Real-Time Global Illumination (screen space)


Light Propagation Volumes (LPV)

- 要解决的核心问题:为了做全局光照(间接光照),其实需要的是在任何一个Shading Point,如果可以立刻得到间接光照到达该Shading Point时,来自所有方向的Radiance是多少
- 认为Radiance在沿直线传播过程中是一个不变的量

- LPV做法:
- 首先将3D的场景分成网格,这些格子用来传播Radiance
- 要知道哪些点作为次级光源
- 要把这些接收到直接光照的点,放进(注入 injection)划分的格子里
- 在三维的网格中传播Radiance
- 渲染

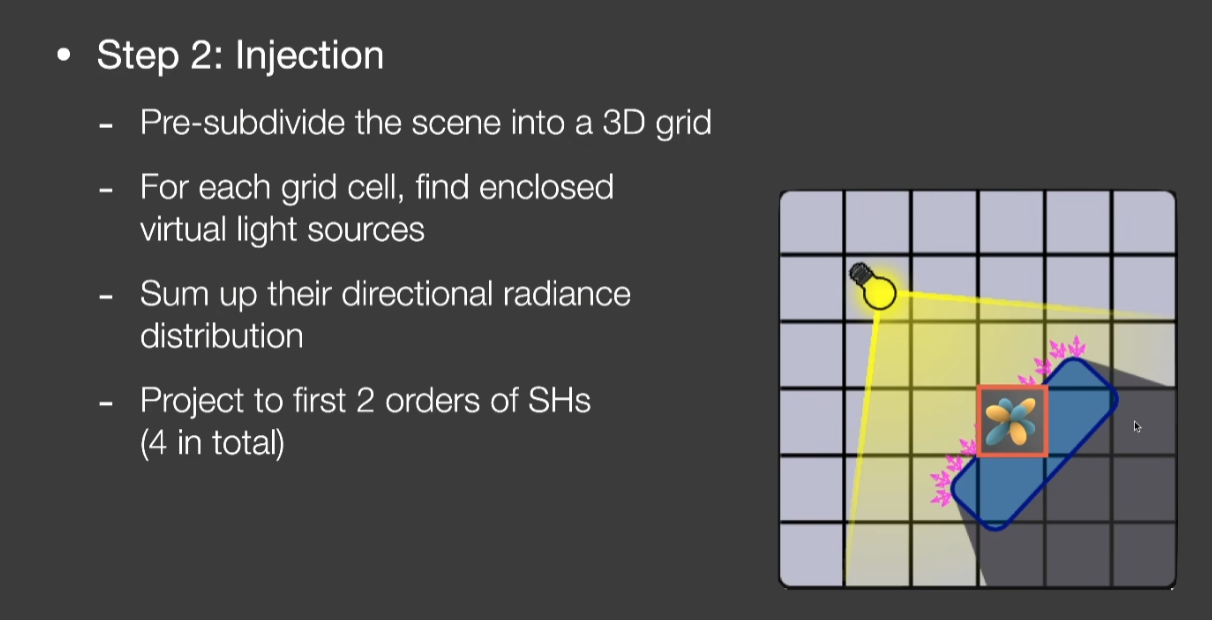


- 具体一点:
- 第一步:生成。用RSM找到场景中直接光照照亮的表面,有多少光源就得做多少RSM。可以降低当做次级光源的表面数量。完成后得到虚拟的光源
- 第二步:注入。工业界一般用一个三维的纹理来定义划分的格子。看任何一个格子内部是否包含了前一步得到的虚拟光源,把所有的格子内部的虚拟光源往各个不同方向的Radiance都算出来再相加,拿SH去压缩它,工业界一般用前两阶来描述这种大概的Radiance分布
- 第三步:传播。一个格子会传播到周围的六个格子上去,对每一个格子都会扩散到周围的六个格子上去,直到最后所有网格稳定下来(迭代四五次,每次迭代是每个格子向周围扩散)
- 第四部:渲染。对于任何一个Shading Point,都知道它在哪个格子里,知道格子后把这格之前接收到的incident Radiance都加起来

- 问题:
- LPV的假设中不考虑Visibility,当物体粒度比格子还小的时候,会出现Light leaking问题
Voxel Global Illumination (VXGI)
- 是一个两趟(two-pass)算法


- 与RSM的主要区别
- 在RSM里次级光源都是每个像素所表示的微小表面,在VXGI里场景是完全离散成微小的格子。像素->体素
- ray tracing -> cone tracing
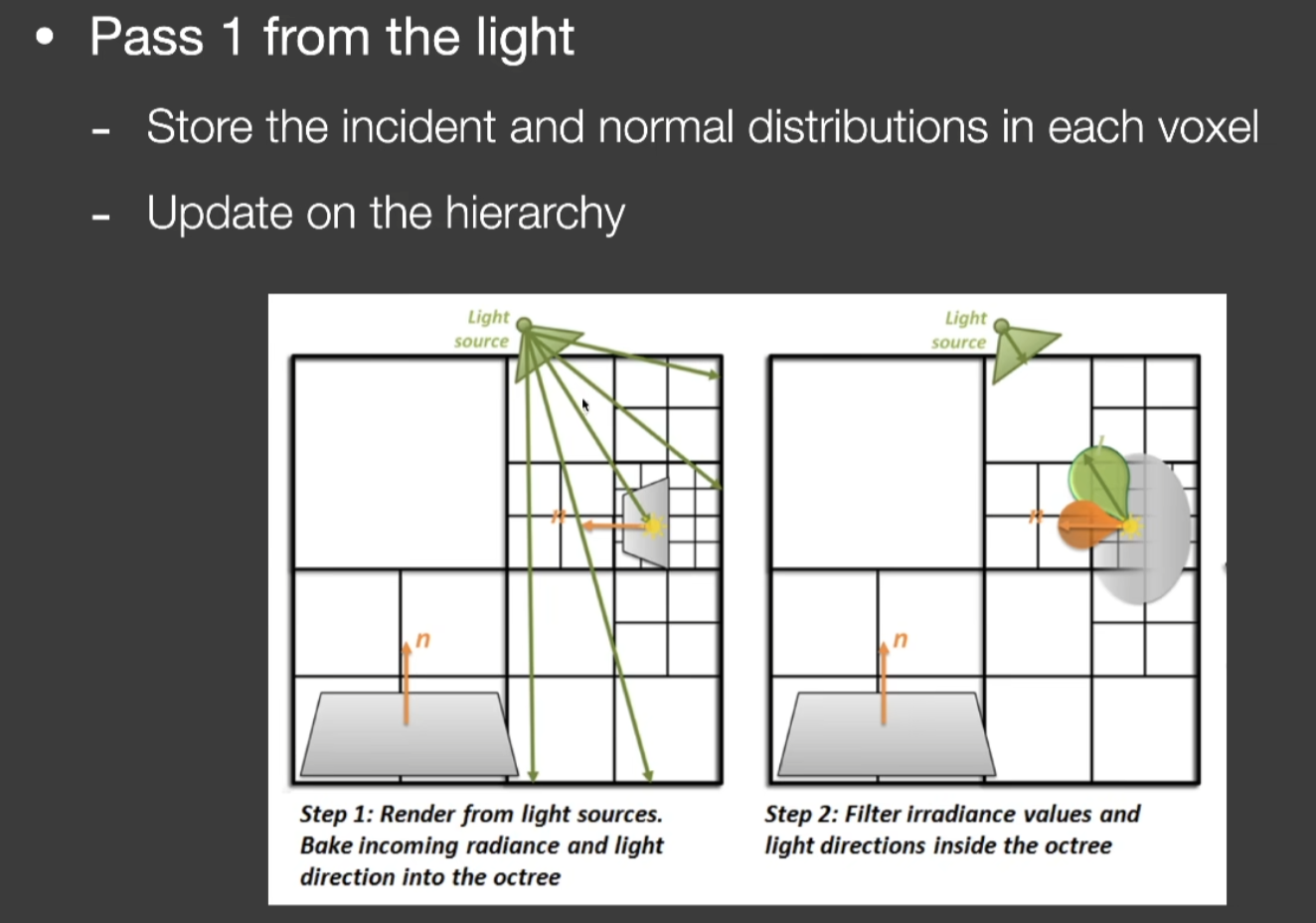
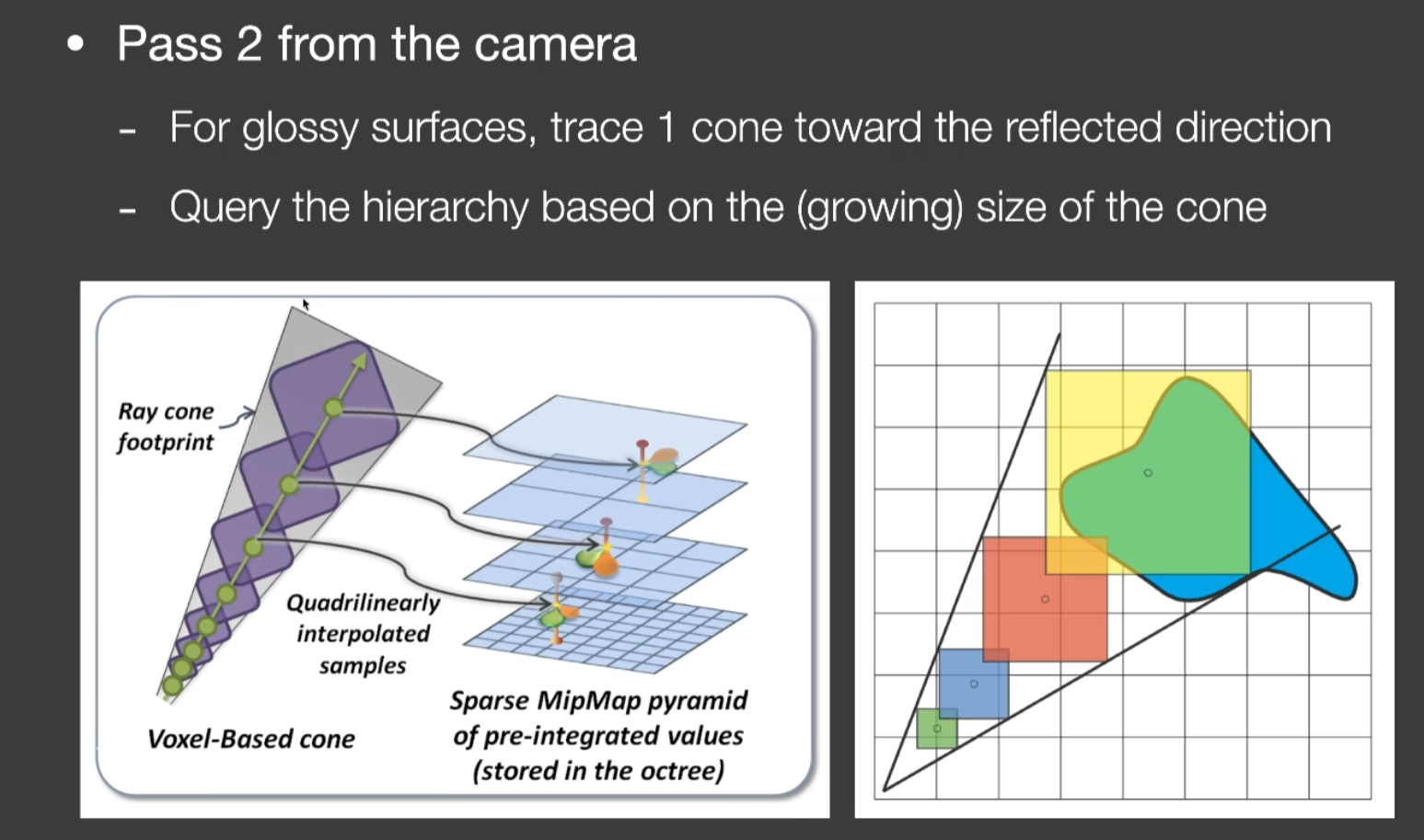

Real-Time Global Illumination(screen space)

- 屏幕空间方法:相当于做图像的后处理,认为起点是只有直接光照
Screen Space Ambient Occulusion (SSAO)

- 常数阴影让物体的相对位置感更强,提升视觉效果
- AO是非常容易实现的

- AO是全局光照的近似
- 在屏幕空间

假设:
- 不知道间接光是什么,假设间接光是一个常数
- 考虑Visibility
AO这种渲染方式在建模软件中叫做 天光
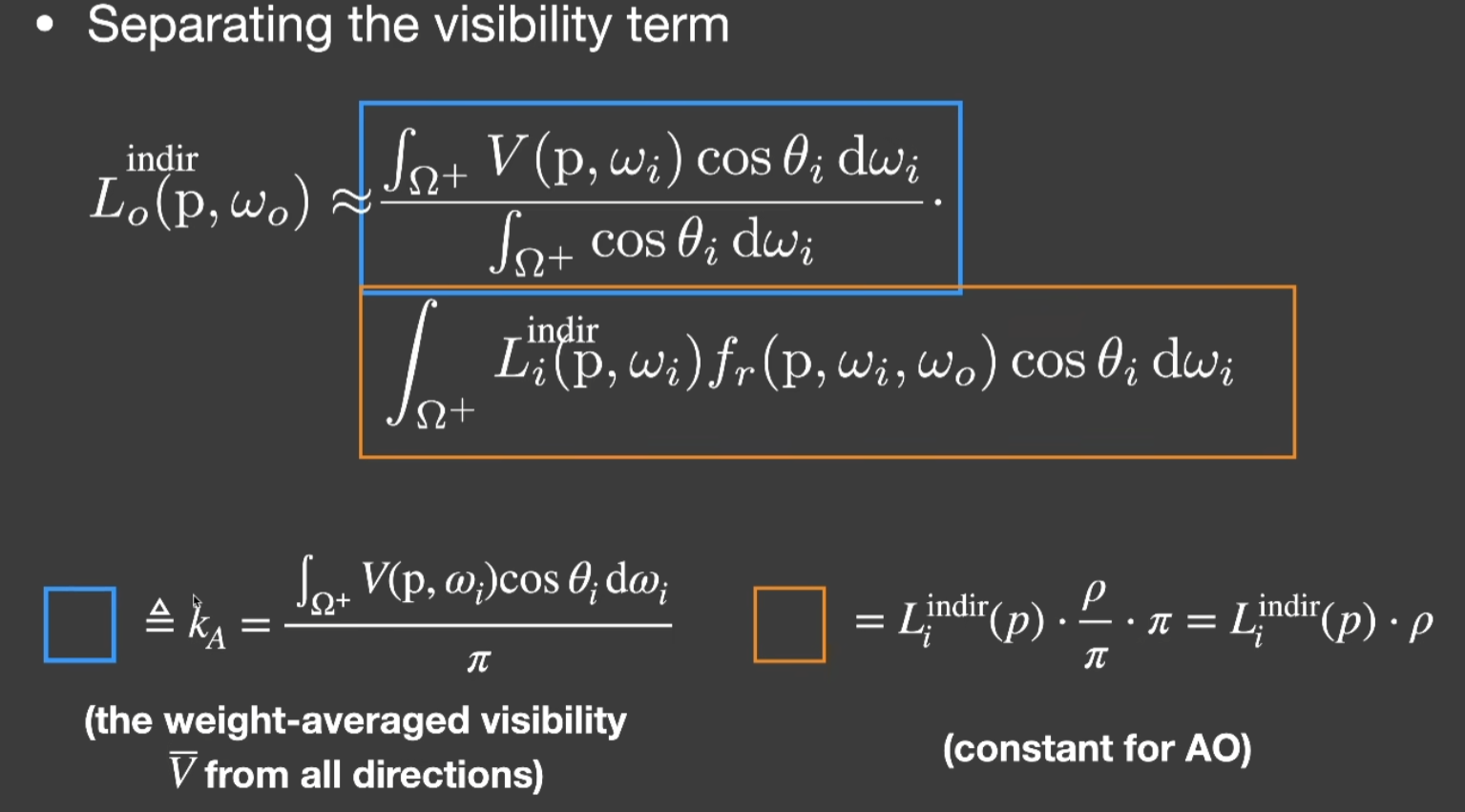
- 从Rendering Equation理解AO是环境光的近似


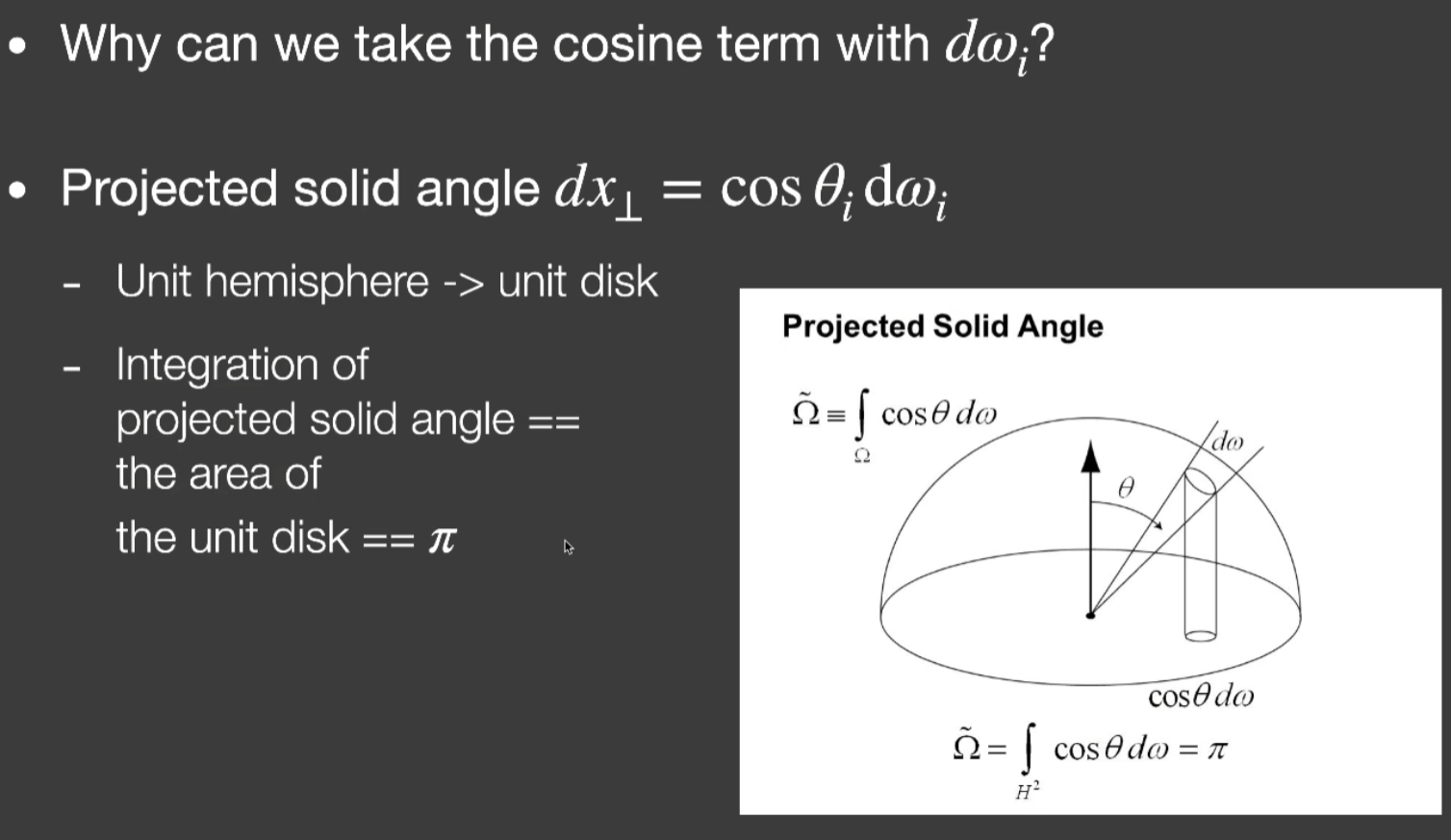

- 实际上AO是一个非常简单的事,只要假设间接光照、物体的BRDF都是Diffuse也是个常数,直接从Rendering Equation拿出来,剩下对Visibility cos的积分
- 加权平均的Visibility在Screen Space怎么做

- Ray tracing一般会考虑在一定距离范围内有无遮挡物
- 但是会造成超过这个范围的却真正会遮挡的物体被忽略
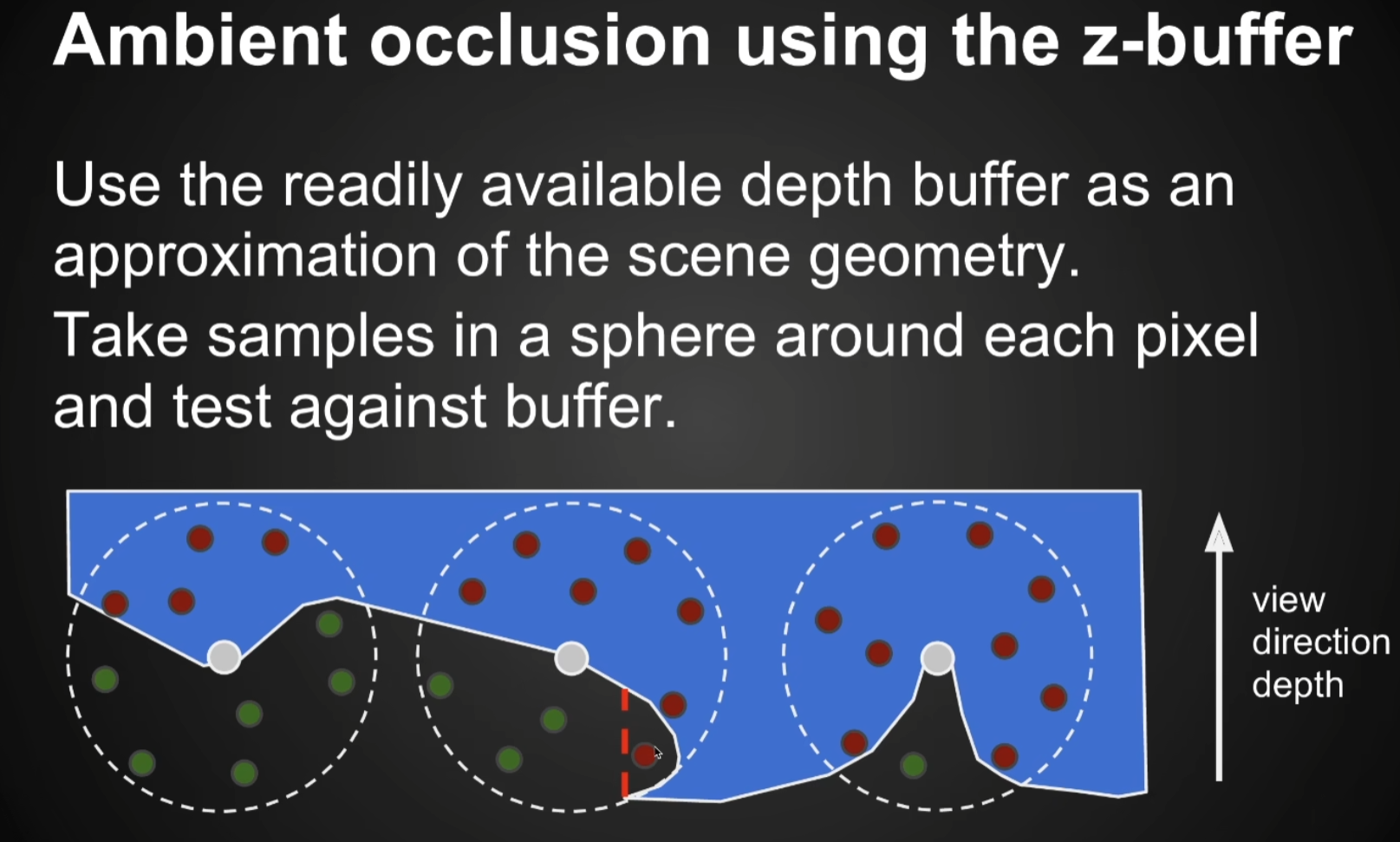
- Screen Space AO并没有这么做
- 它假设任何一个Shading Point,都往周围一个半径r的球里面去采样很多的点,判断这个球的体积内随机撒的点能不能被看到
- 结合从摄像机获取的深度图,来判断物体能否被看到

- 考虑Visibility都是法线所在的半球
- 在AO那个时代,还不能假设Camera Ray渲染出来的场景又有深度又有Normal,可以认为有深度,得不到法线方向。
- 不知道法线方向就不知道哪个半球该去考虑,因此考虑整个球。而正常情况下一个平面必然有一半看不到,所以对任何一个几何做这么一个假设:在打在全球里面的点只有看不着的点(红点)个数过半的情况下,才开始考虑AO问题
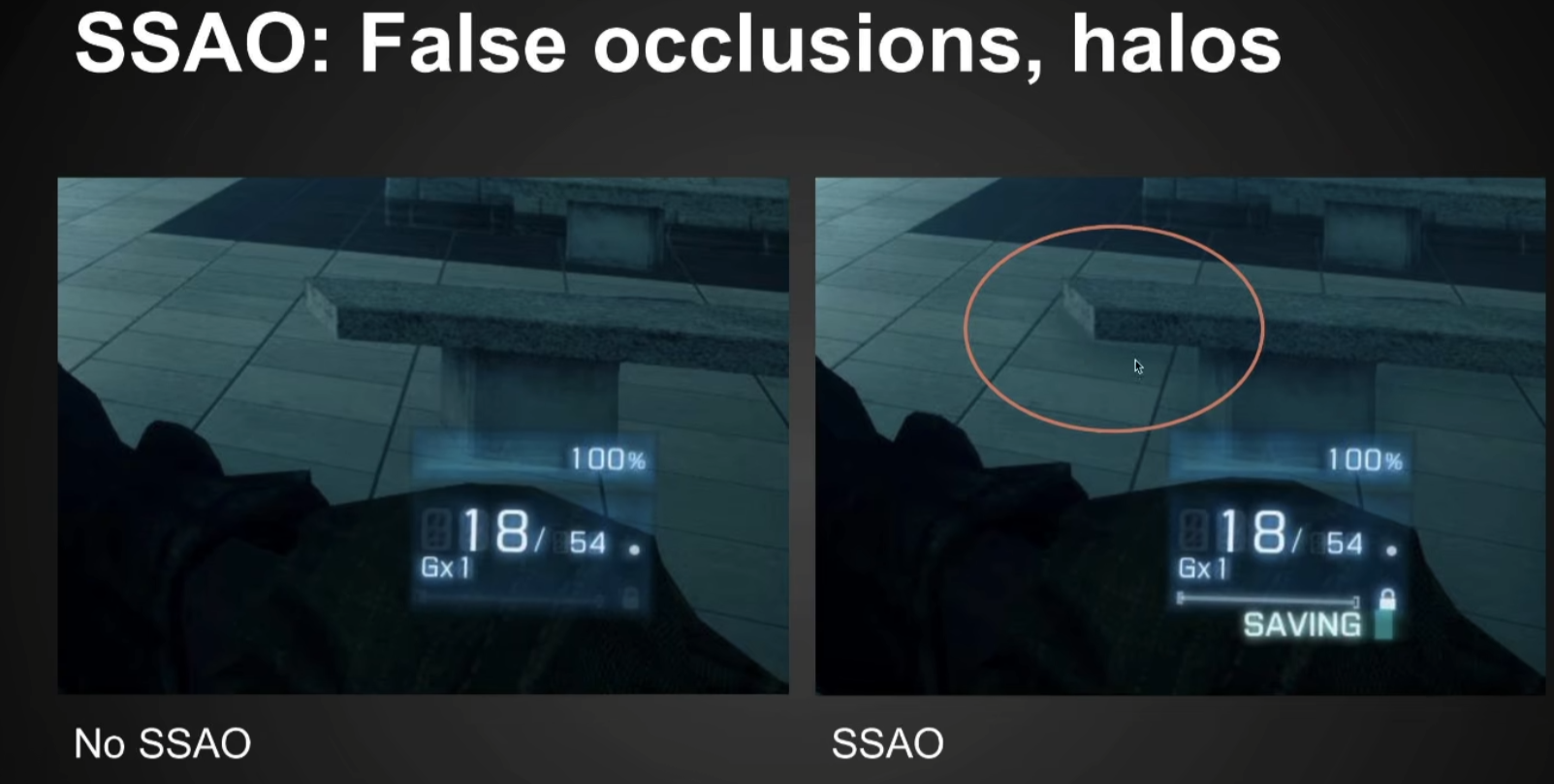



- 采样点越多效果越好,但为了速度,不能有太多的Sample,做法是用少量的Sample先得到一张Noise的AO结果,再对它DeNoise把它模糊掉
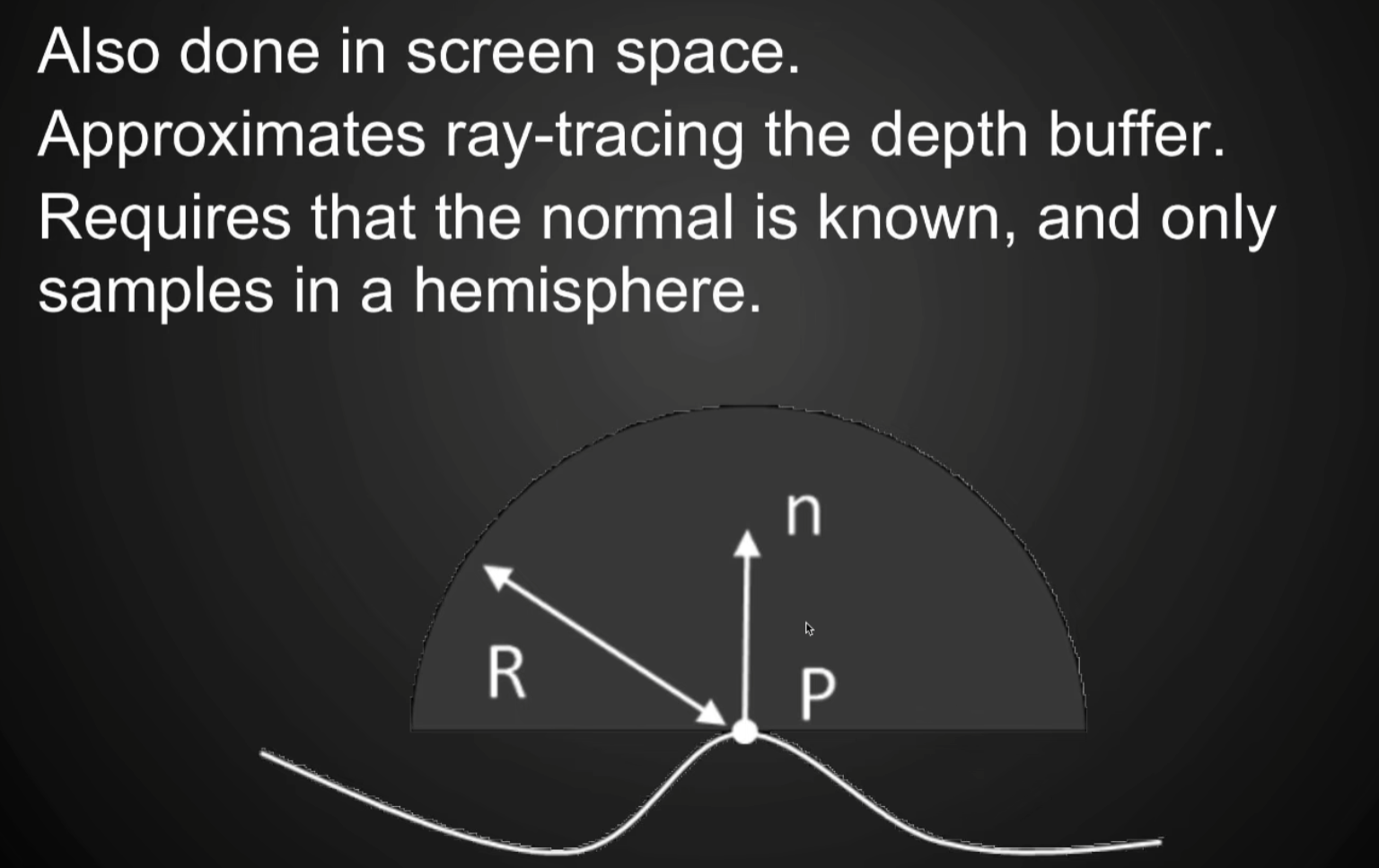
- 在现在有法线的情况下,不需要SSAO做那么近似的假设,并且可以对各个方向做加权,得到更准的值

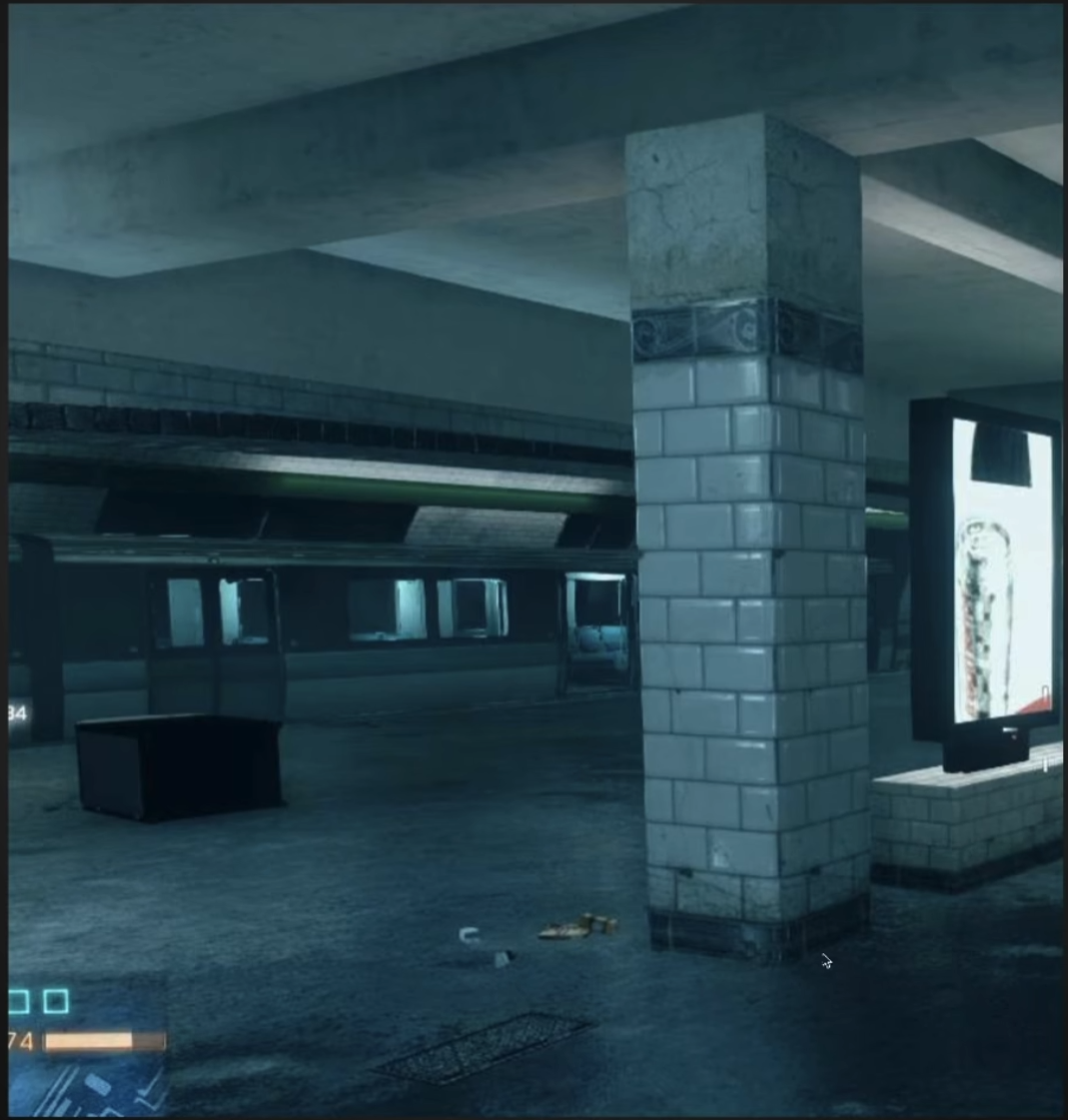


- HBAO比SSAO要好一些,就是因为它真正考虑了一定范围r的半球
Lecture 9 Real-Time Global Illumination (screen space cont.)
Screen Space Directional Occlision (SSDO)


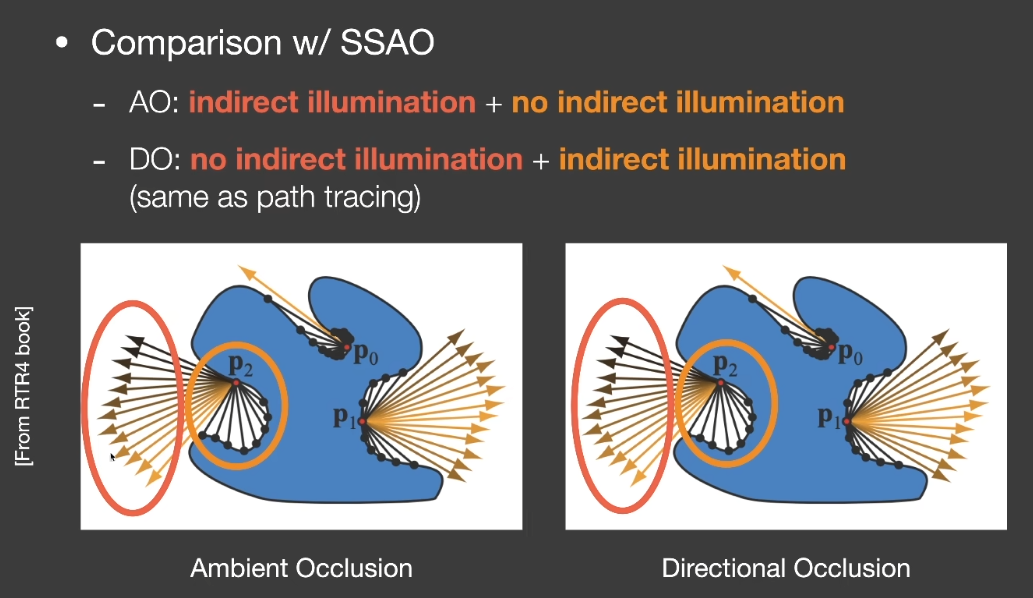

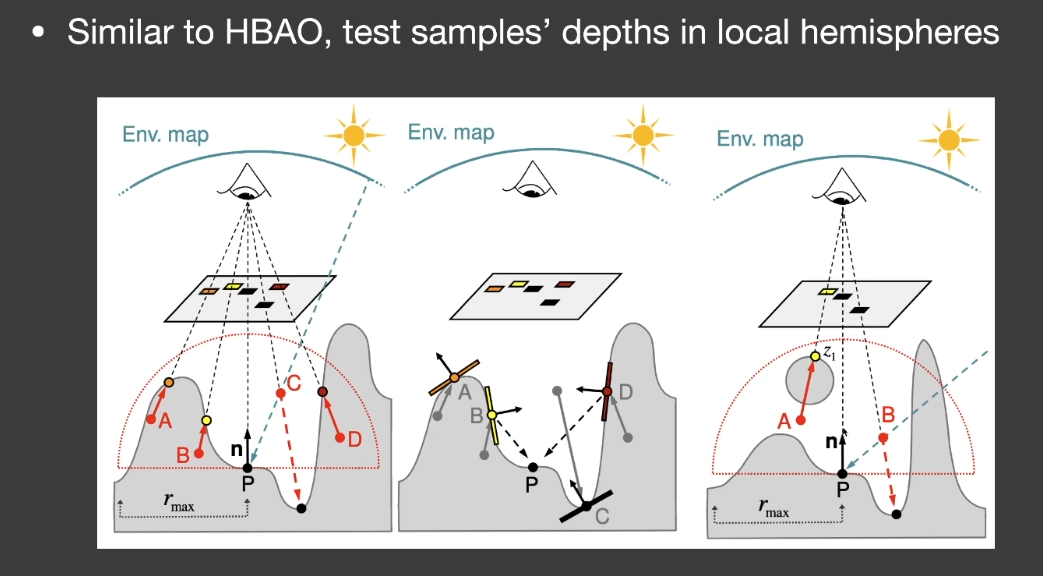

Screen Space Reflection (SSR)

- 实际上是在屏幕空间做光线追踪

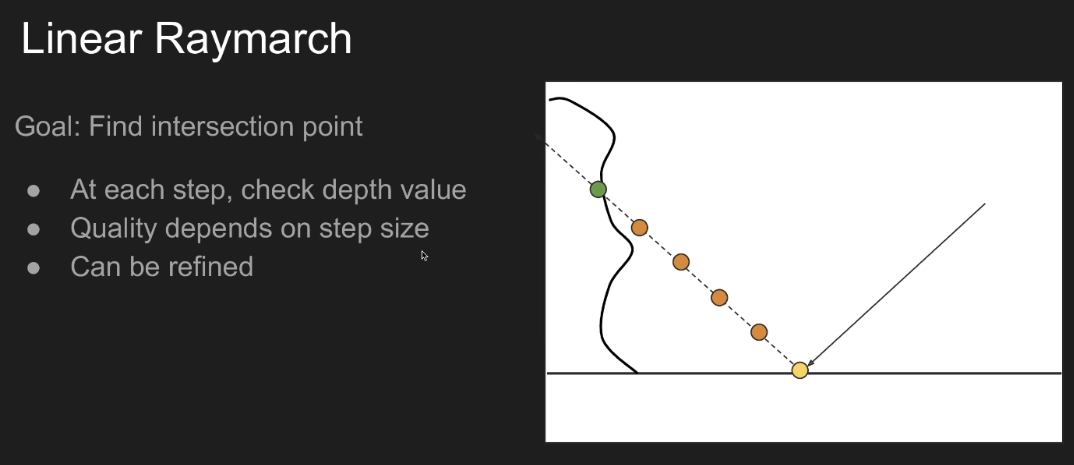
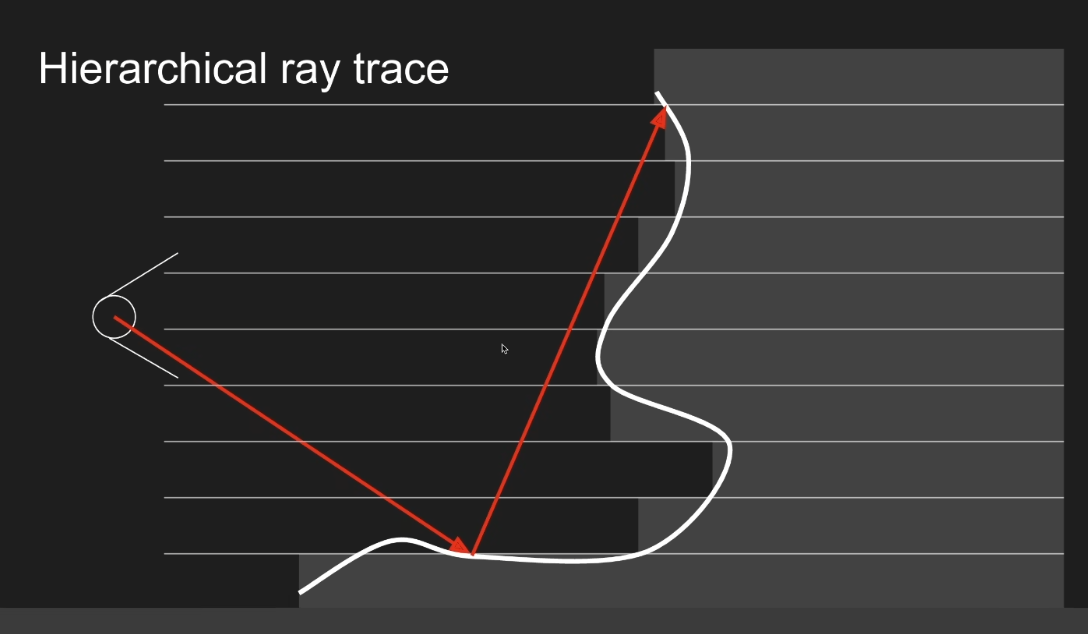
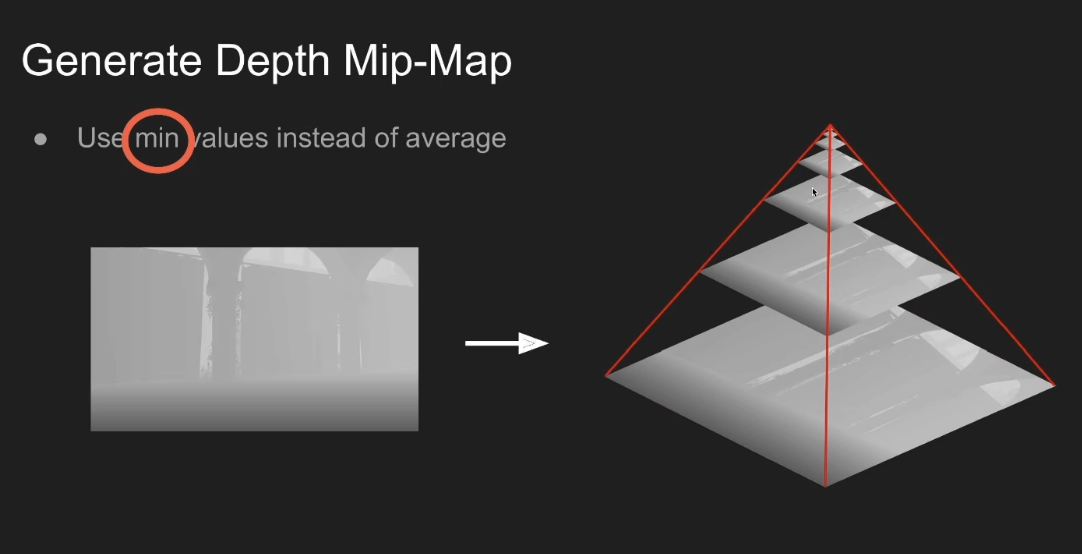

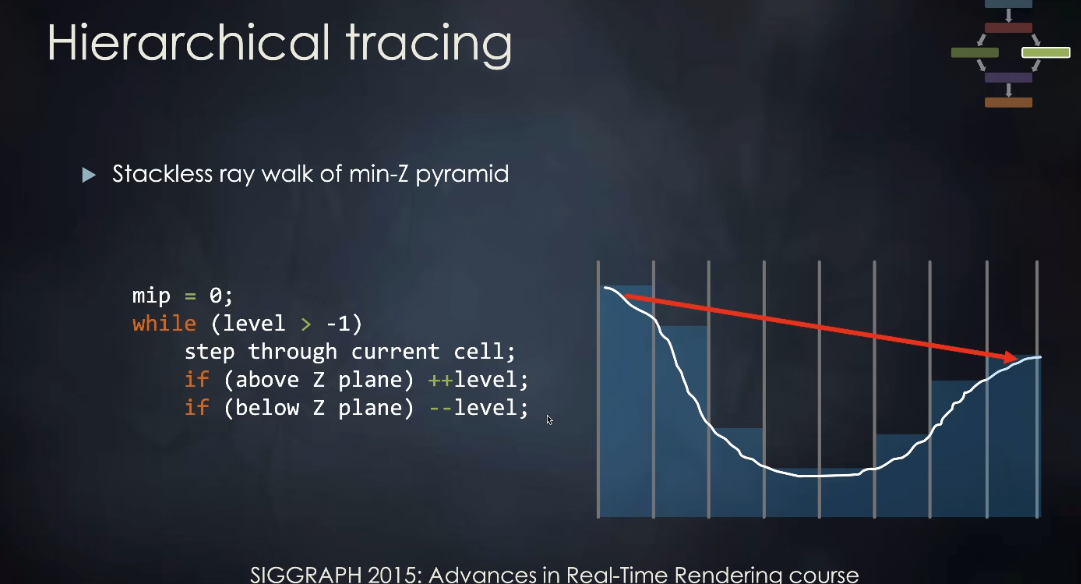
- 动态决定步长




Lecture 10 Real-Time Physically-Based Materials (surface models)
- Microfacet BRDF
- Disney principled BRDF
- PBR概况:




Microfacet BRDF
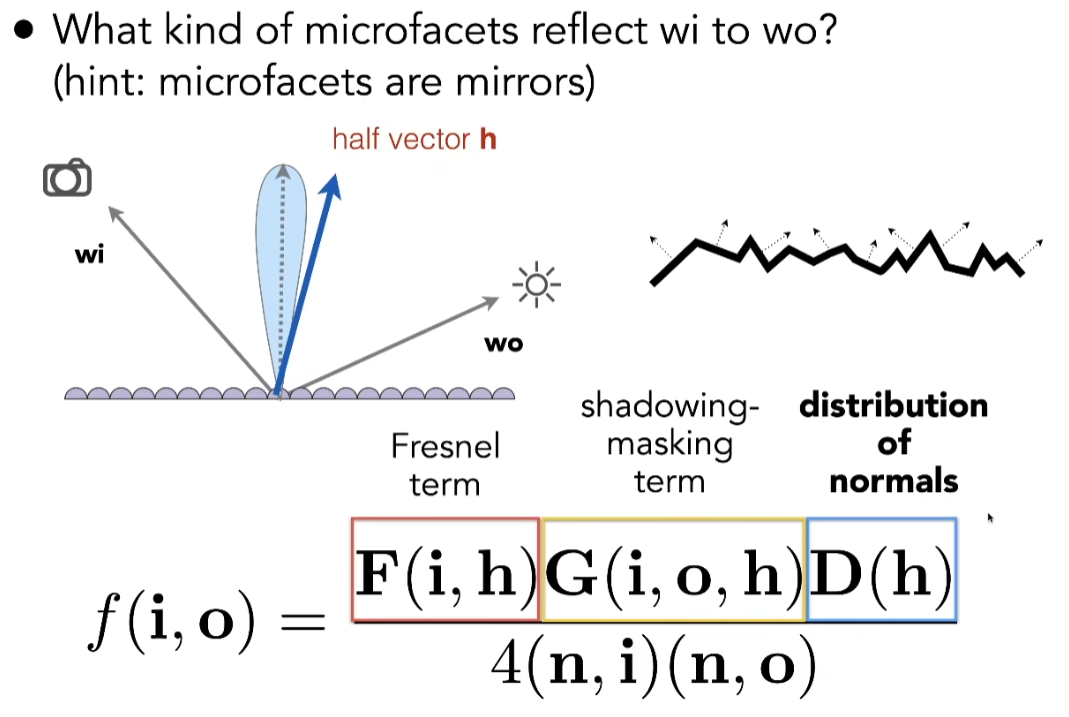
- Fresnel项告诉我们有多少百分率的能量会被反射

- 有多少能量被反射取决于入射光的角度
- 入射方向与法线几乎垂直,这时反射是最多的
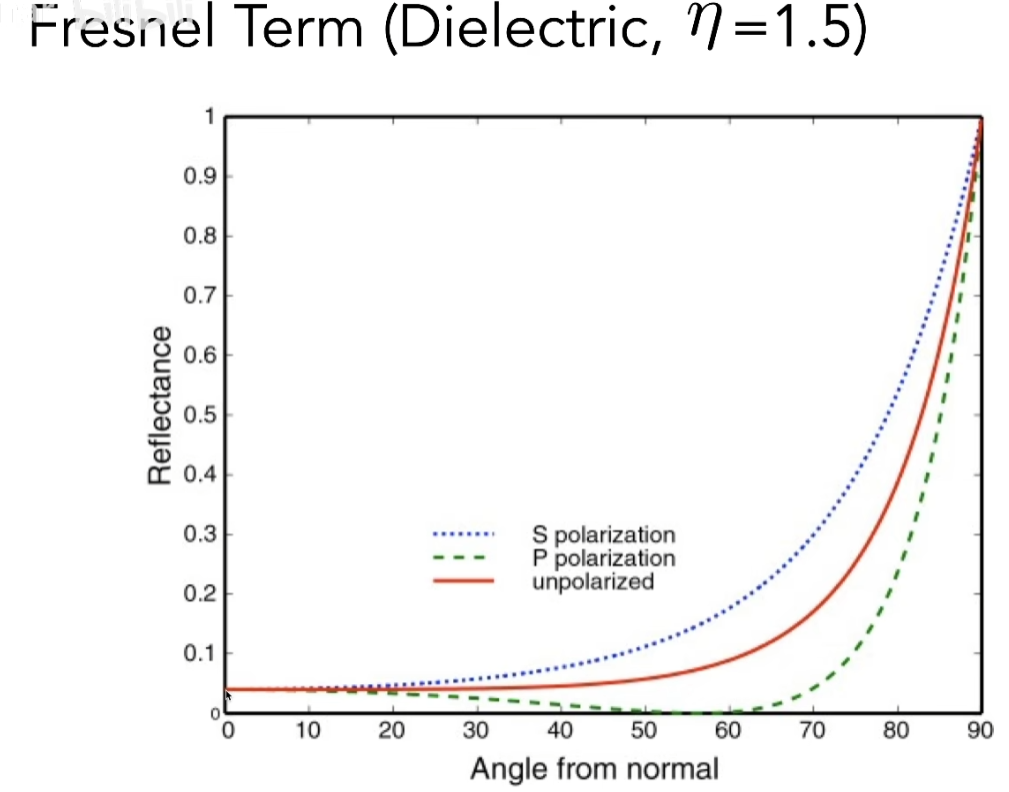
- 根据入射角不同,有多少能量会被反射
- 对于绝缘体,从正上方看,很少能量被反射,基本上能透过去,如水面、镜子;从掠射角度看,能看到更多的反射
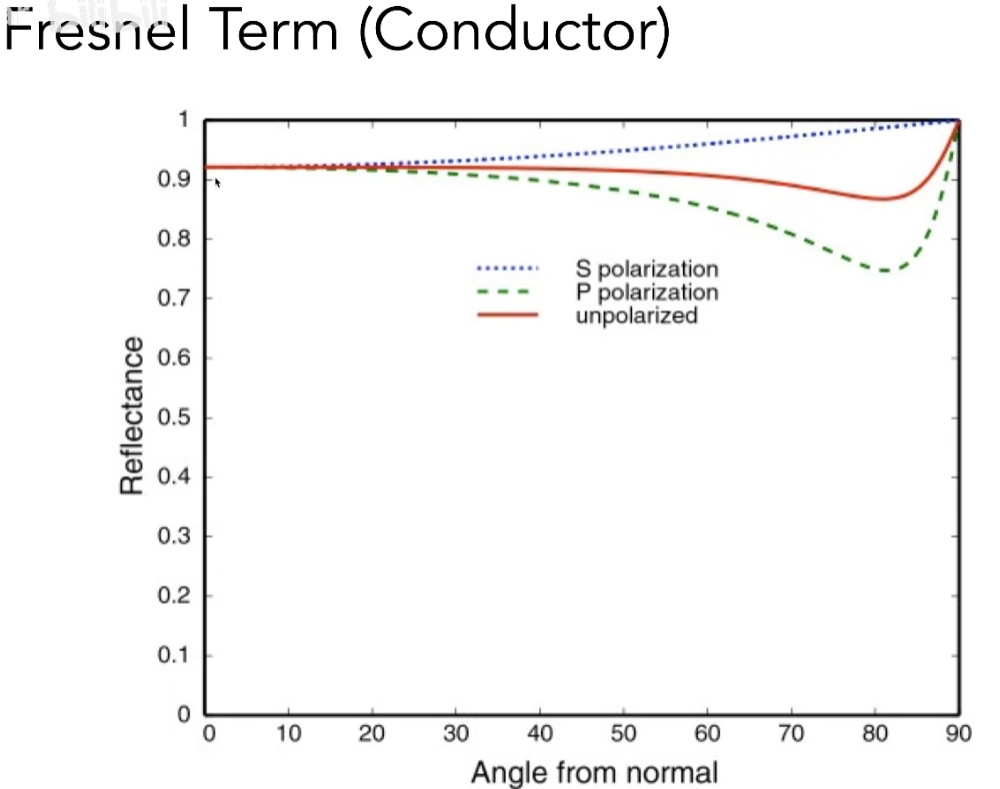
- 对金属来说,基本上符合这个曲线,整体反射能量会高很多

- 在物理上会考虑光线的S极化和P极化,以及两种极化的综合效果
- 但是又不太对,因为要考虑空气到物体表面各自的介质折射率,又要考虑入射角
- 有一个简单的估计,基础反射率R0,加上某种曲线,一开始是R0,拉到掠射角1
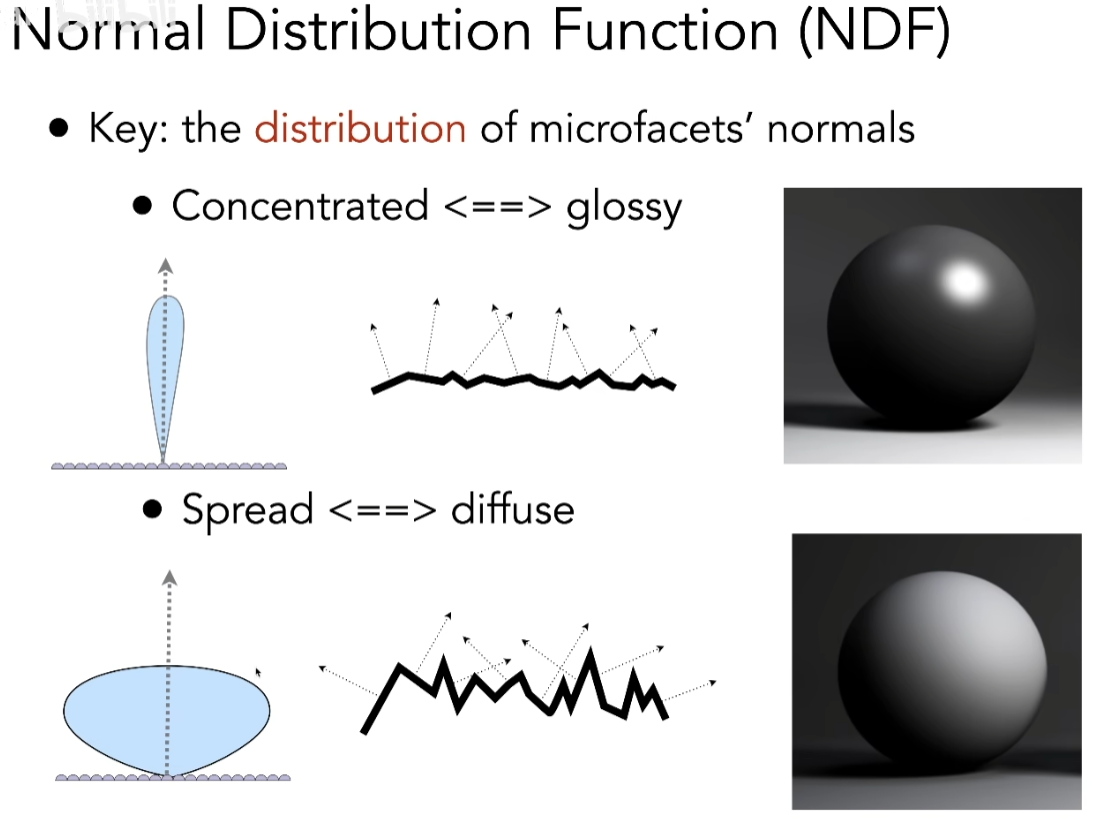
- 重要的是微表面各自的法线分布(NDF)
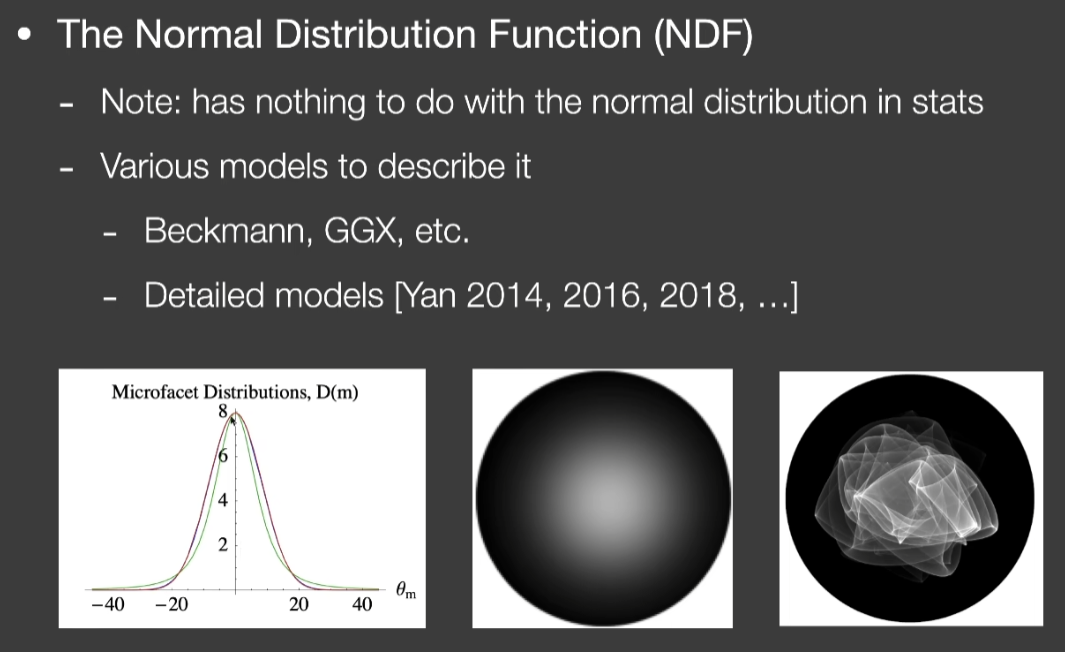
- 二维的法线分布函数模型
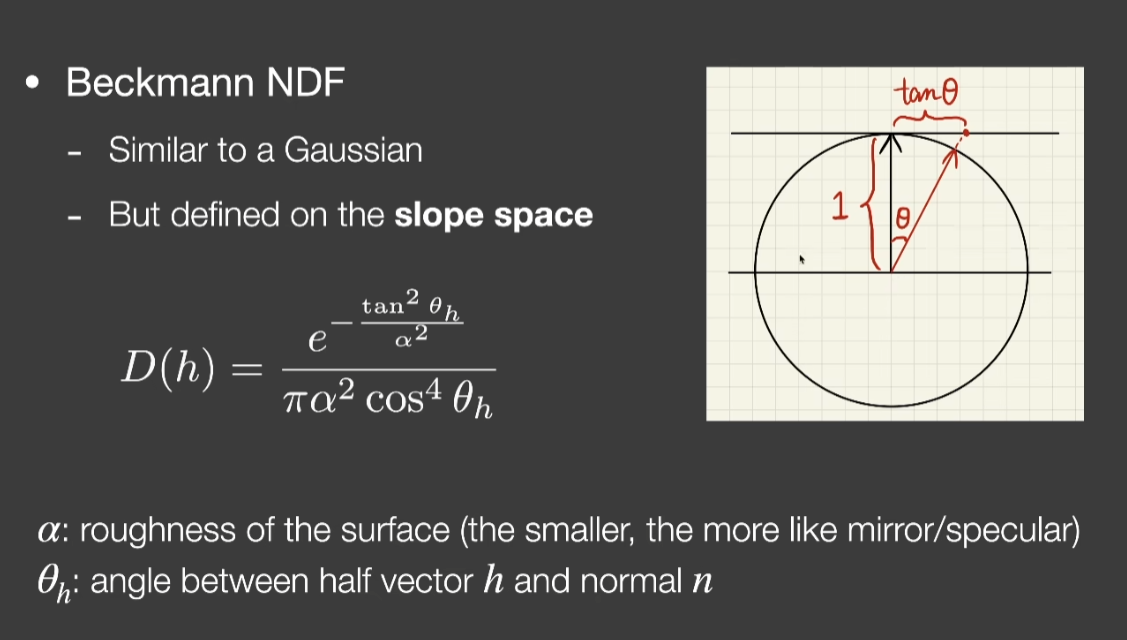
- 法线方向h的函数
- 高斯函数是正态函数更通用的解释,也就是中间值大,往两边衰减的形状
- α一定程度上描述不同材质表面的粗糙程度,越小表示越不粗糙
- tan2θ:因为BeckmannNDF是定义在坡度空间上,θ可以无限接近90°但不会超过90°,也就是不会出现面朝下的微表面
- 分母一系列计算是为了做归一化,为了在单位球投影变成单位圆后,在这个域上积分成1,这个单位圆的覆盖是x[-1, 1]y[-1, 1]
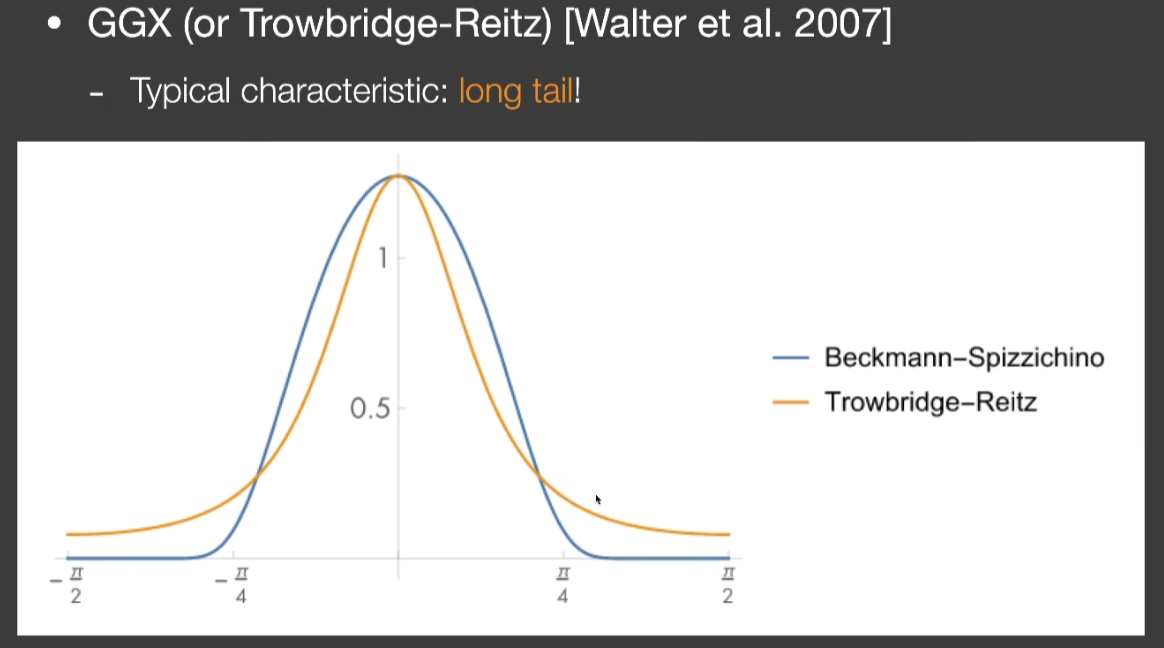
- “长尾”性质:能量衰减到一定程度后,衰减速度会放缓,带来一种自然的效果
- 对比Beckmann,高光的周围,高光不会消失,形成光晕的效果

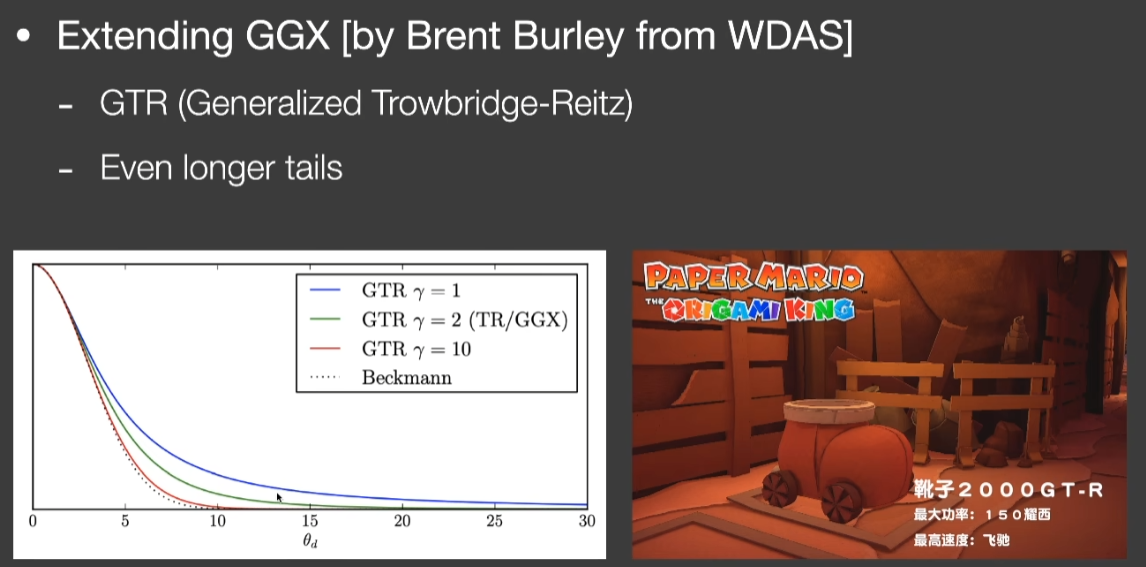
- 希望”尾巴”更长
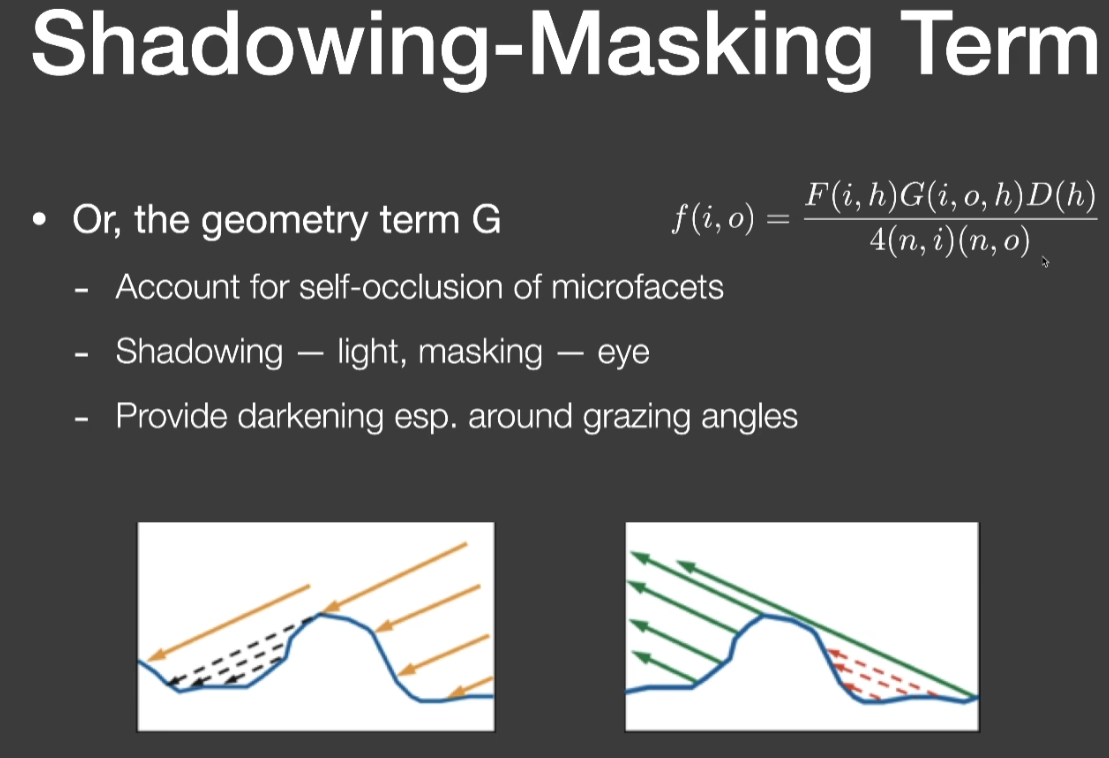
- 又叫”Geometry项”,G
- 解决微表面自遮挡问题
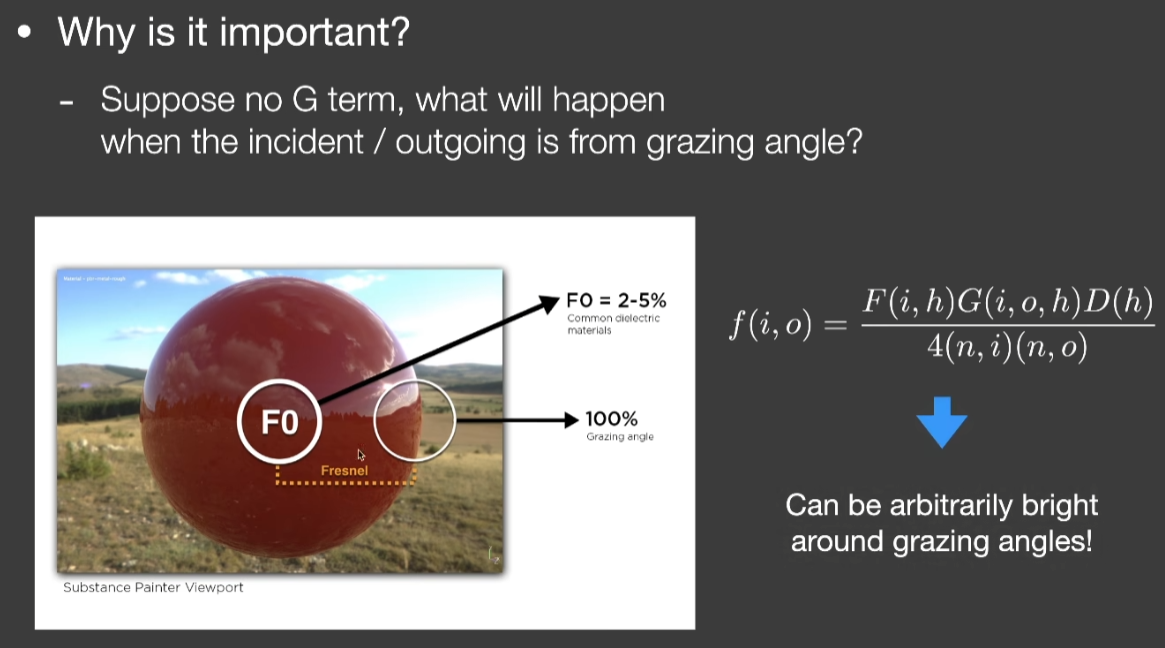
- 避免在Grazing angle的情况下得到非常亮的结果,是不符合事实的
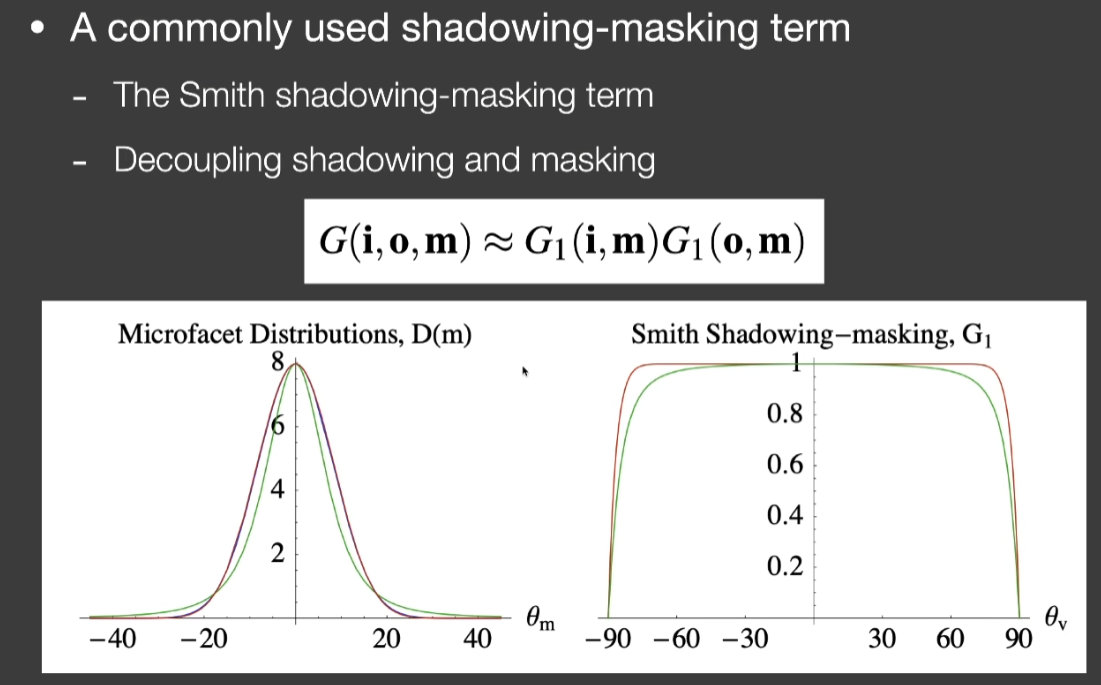


- 越粗糙的表面,光线多次弹射的占比越大,损失的能量越多
- 想办法把丢失的能量补回去
- 基本思路:被遮挡意味着必然会继续弹射,直到被弹射出去
- 因此有了近似方法Kulla-Conty,通过一种经验形的方式去补全多次弹射丢失的能量




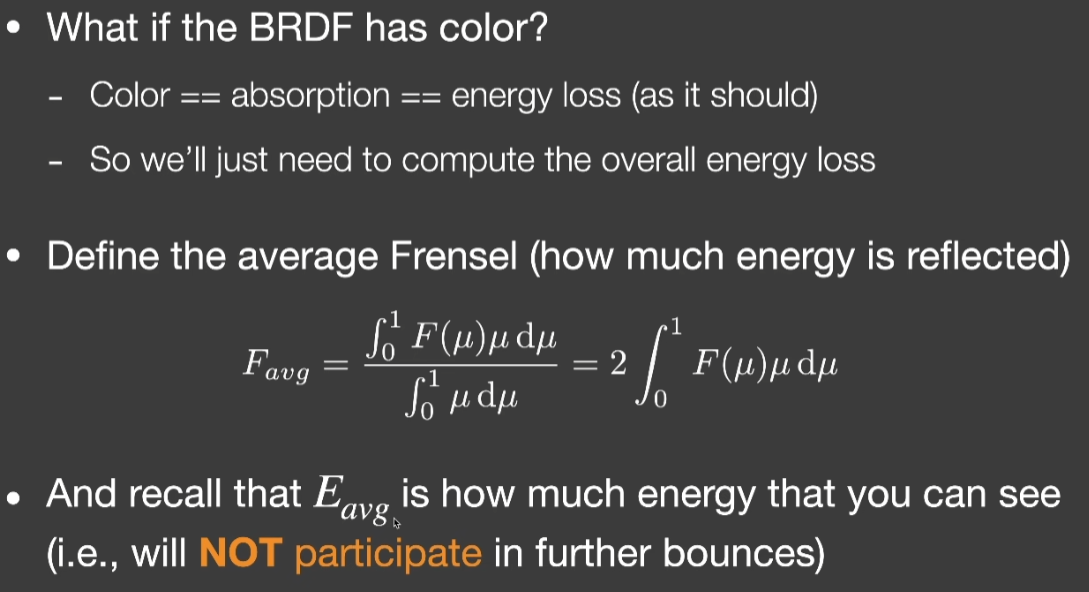


Lecture 11 Real-Time Physically-Based Materials (surface models cont.)


Shading Microfacet Models using Linearly Transformed Cosines(LTC 线性变换余弦)
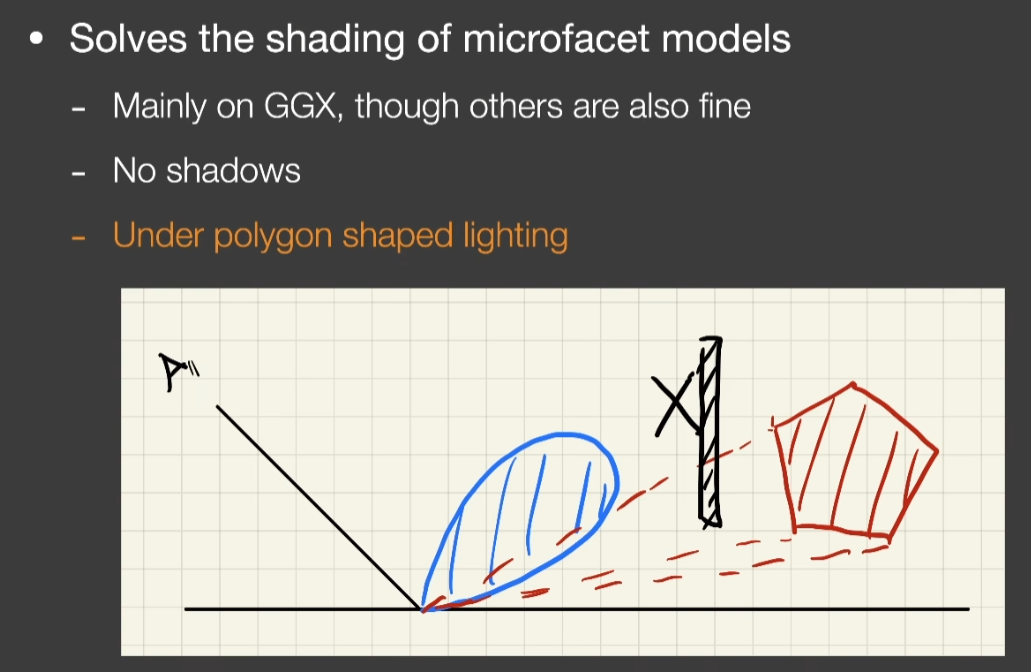
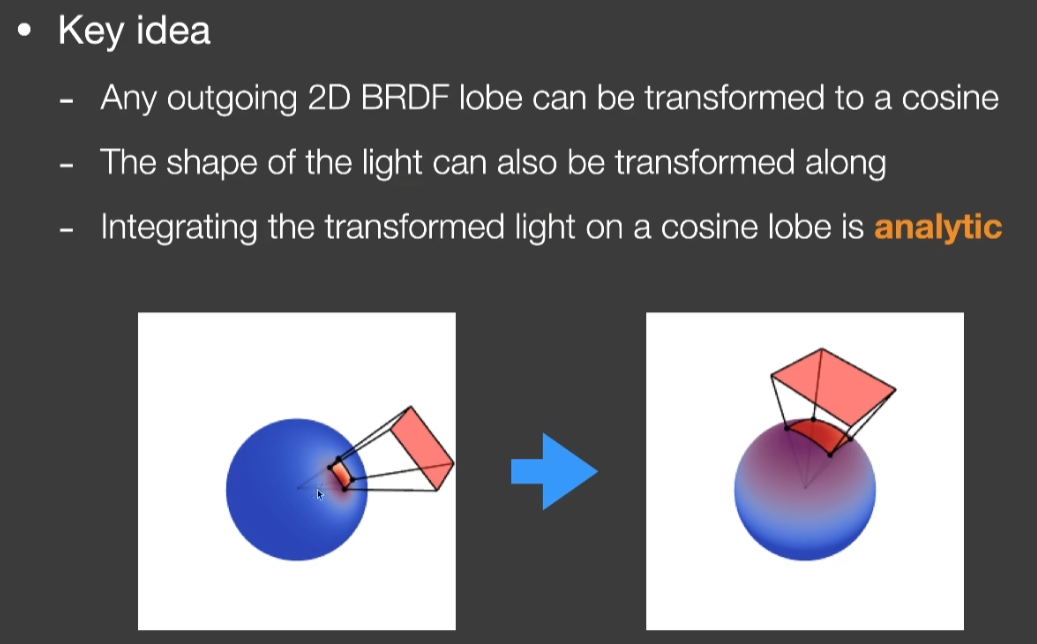
- 把任意的BRDF lobe在任意的多边形Shading转换成了在一个固定的Cosine下对任意的多边形光源进行积分的问题,这个积分是有解析解的
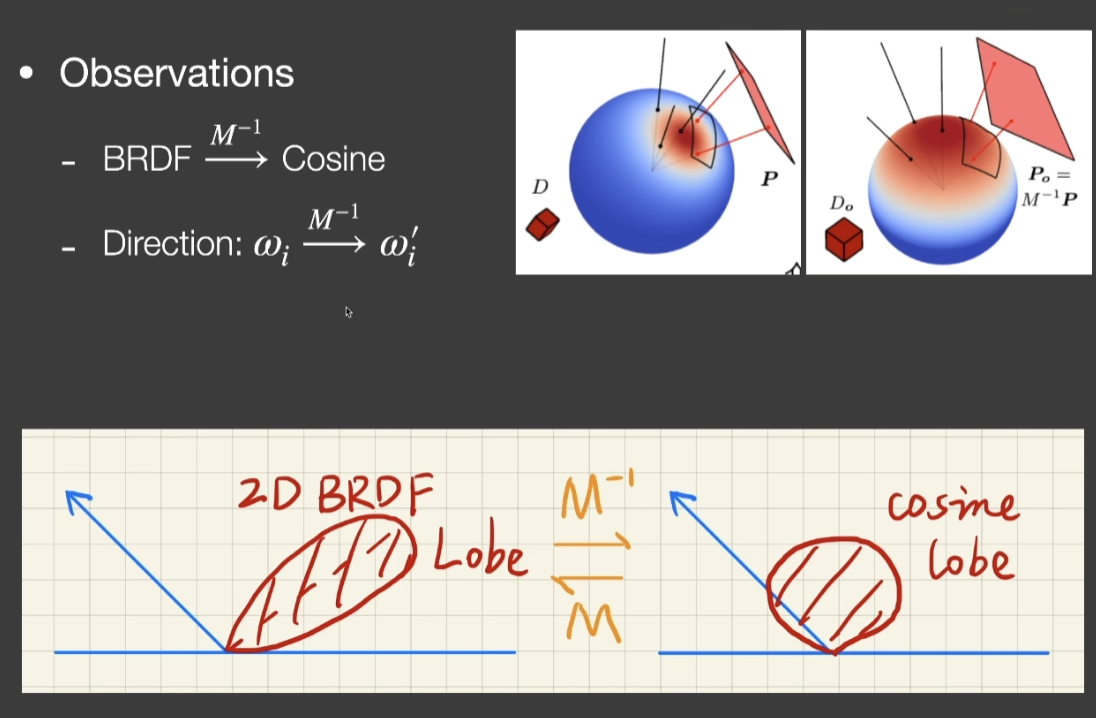


Disney’s Principled BRDF
Why is it needed?
- 微表面模型并不擅长表示真实的材质
- 微表面模型不好用,PBR模型参数多半是物理量相关,对于艺术家不友好
High level design goal
- artist friendly
- 不保证物理完全正确
- 认为基本上Disney’s Principled BRDF还是PBR模型
“principled”设计原则
- 不使用物理量
- 不希望有很多参数
- 参数最好是0到1范围
- 必要时允许超过范围调整参数
- 某些参数的组合情况不会导致程序崩溃或效果难看
How does it work?
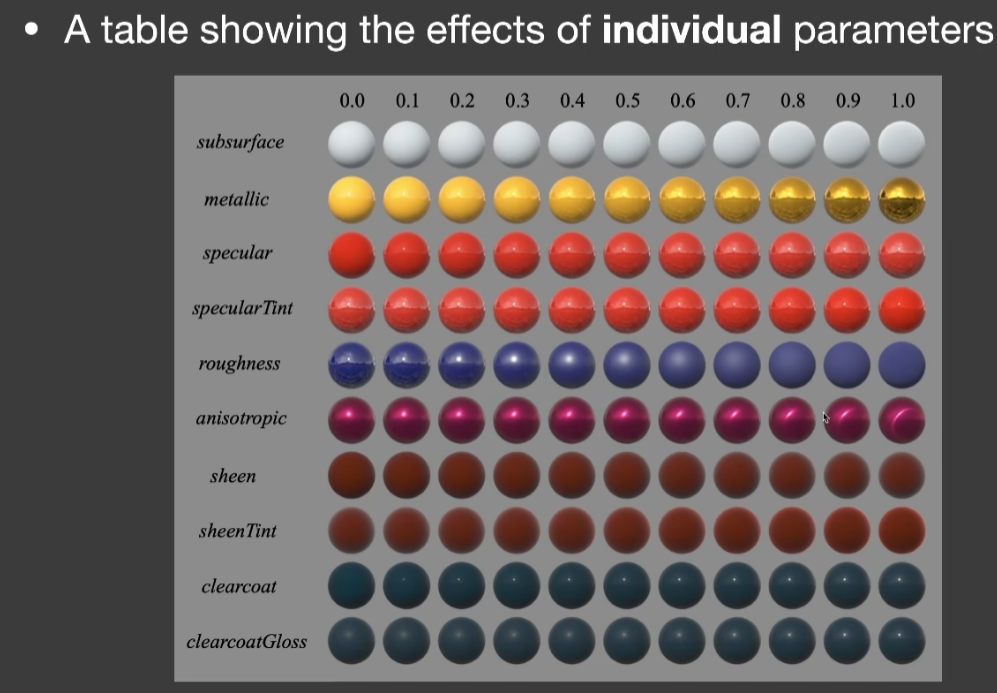
- subsurface
- 次表面反射
- 光线能够进入物体,并且从另外一个地方打出去
- 在BRDF上给人一种比Diffuse还要平的效果
- metallic
- 金属度
- specular
- 相当于Blinn-Phong模型里的ks,相当于控制有多少镜面反射的内容
- specularTint
- 颜色是更偏白(0),还是更偏底下材质的颜色(1)
- roughness
- 粗糙程度
- anisotropic
- 各向异性程度
- sheen
- 在Grazing Angle下看物体表面,有一种雾化效果
- sheenTint
- 希望长出的”绒毛”更偏白还是偏材质颜色
- clearcoat
- 透明的层,镀膜
- 类似木头上刷清漆的效果,包裹了一层糖衣
- clearcoatGloss
- 光滑程度
- Pros and Cons
- 易用
- 功能强大
- 实现复杂
- 并不是基于物理的,牺牲了物理的准确性,但不是重要问题
- 10维的参数空间,参数空间越大,越容易冗余
Non-Photorealistic Rendering(NPR 非真实感渲染)
- 等同于风格化
- 在实时渲染中意味着快速、可靠的风格化

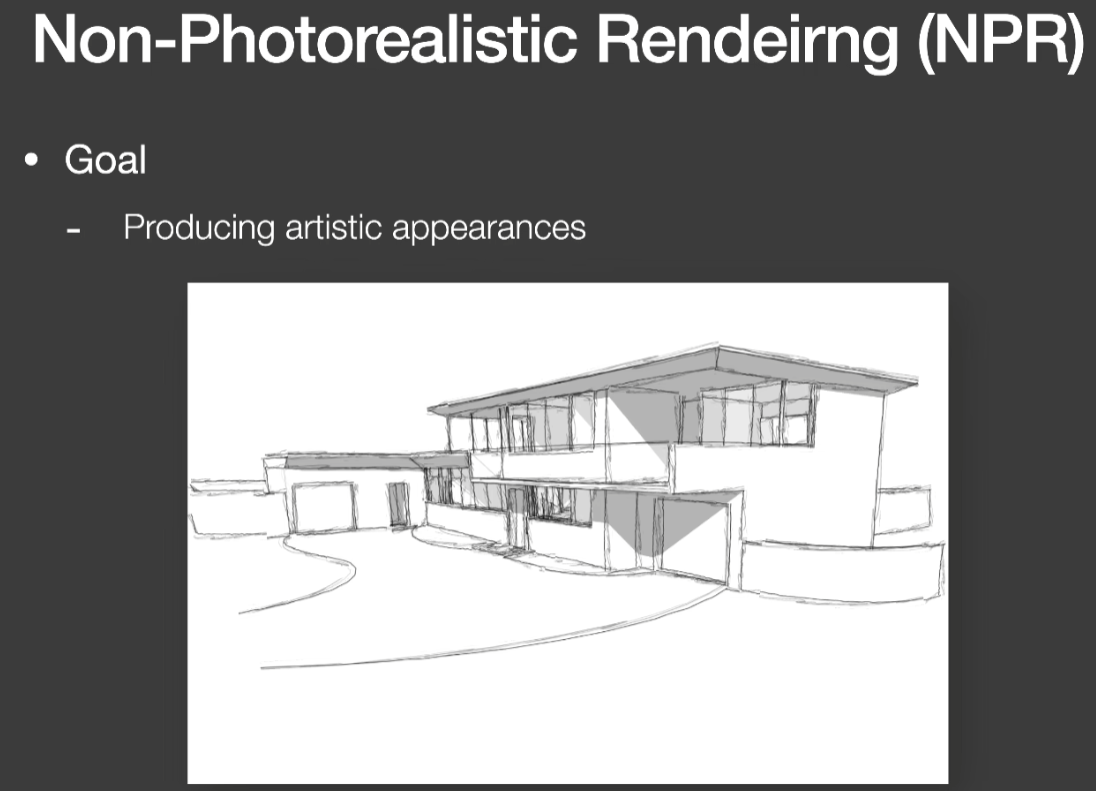
- NPR研究思路
- 从真实渲染出发
- 把真实渲染变成非真实
- 分析真实效果,转换成渲染操作

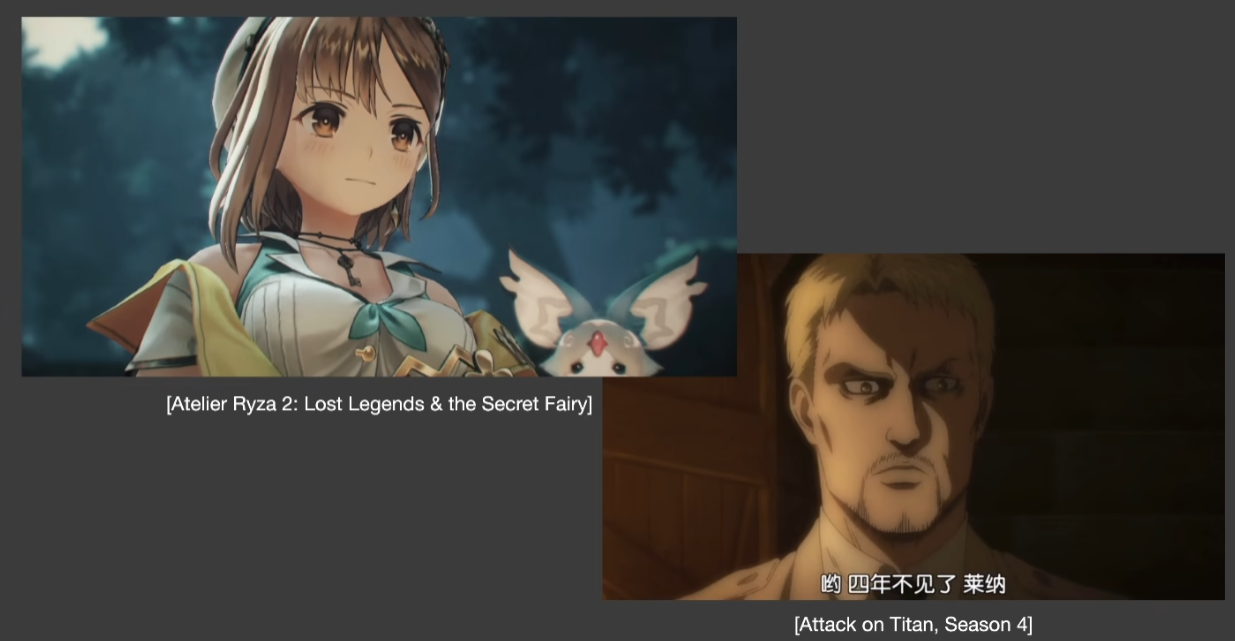
- What are Styles?


- 轮廓渲染
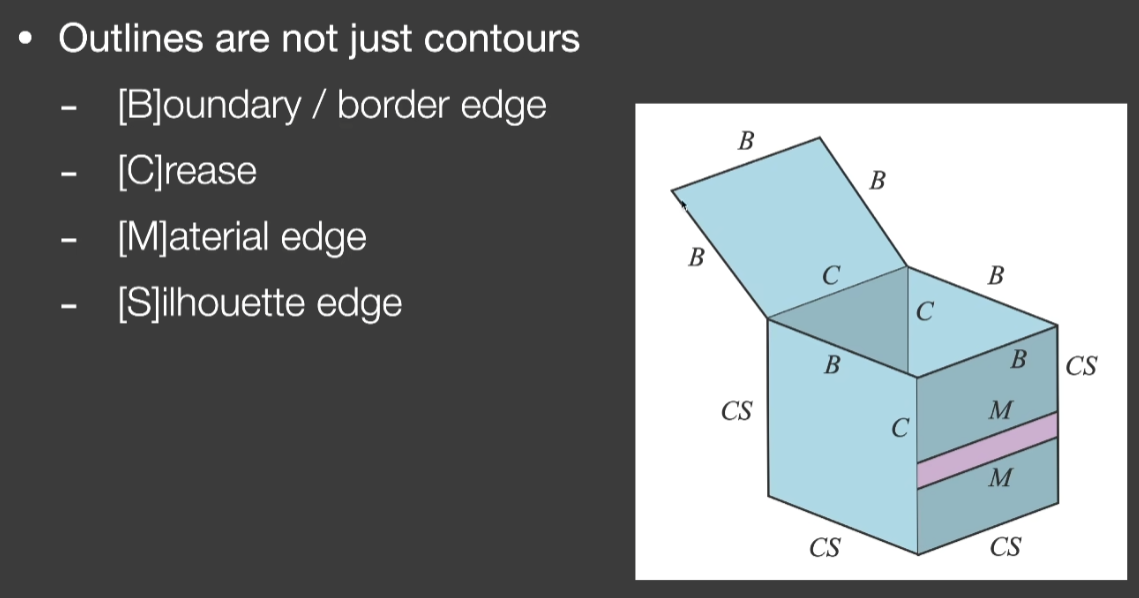

- 渲染上
- 用角度阈值规定描边区域
- 粗细不一样
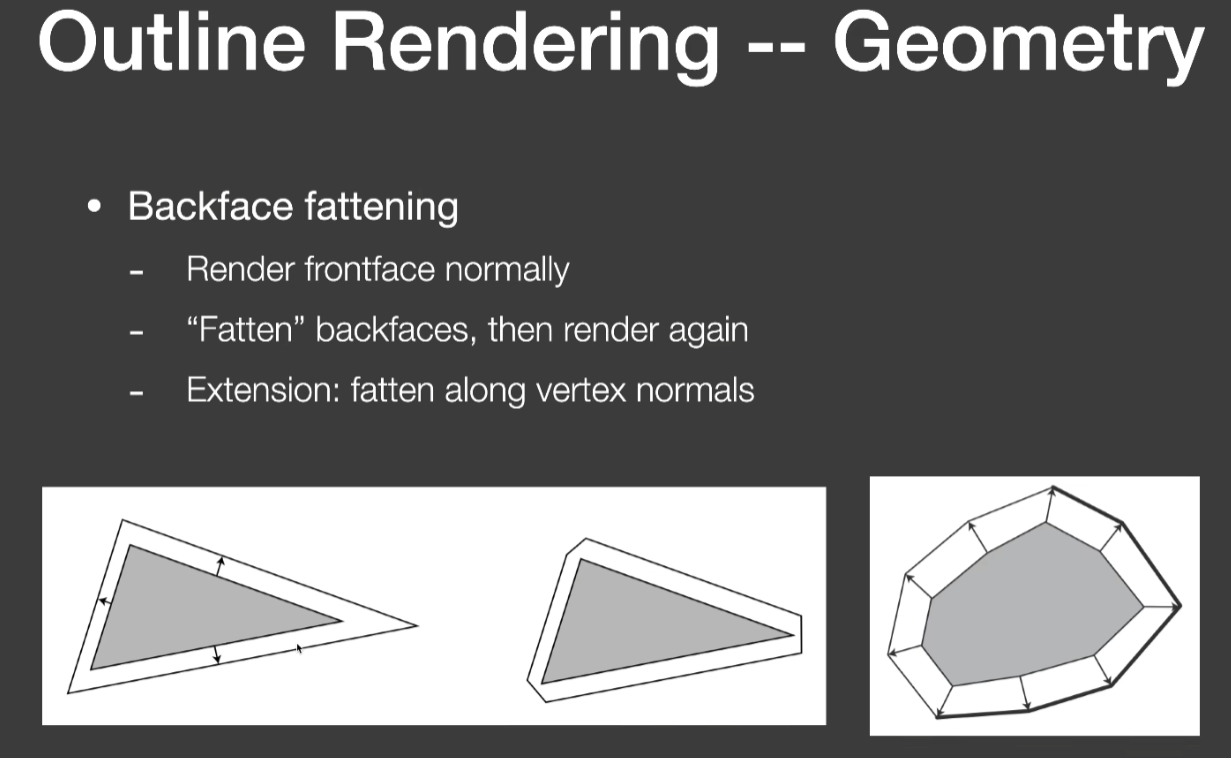
- 几何上
- 把背面的面扩一圈


- 图像后处理上
- 锐化做的就是找到图像上的边界加回到原图上,起到强调的效果
- 色块

- 做一个阈值化

- 可以不是二值化,可以多值化

- 可以在不同的部分做不同的阈值化

- 分析不同点应该用什么样的密度
- 保证不同点之间密度变化过程中,笔触的连续,所以需要设计不同密度的纹理

- 防止距离变远时uv缩小、密度变大、图像变暗,做一个MipMap
- Some Notes
- NPR is art driven
- need the ability to “translate” artists’ needs into rendering insights
- Communication is important
- Sometimes, per character, even per part
- Photorealistic models are super important in NPR

Lecture 12 Real-Time Ray-Tracing 1

RTRT is Happening



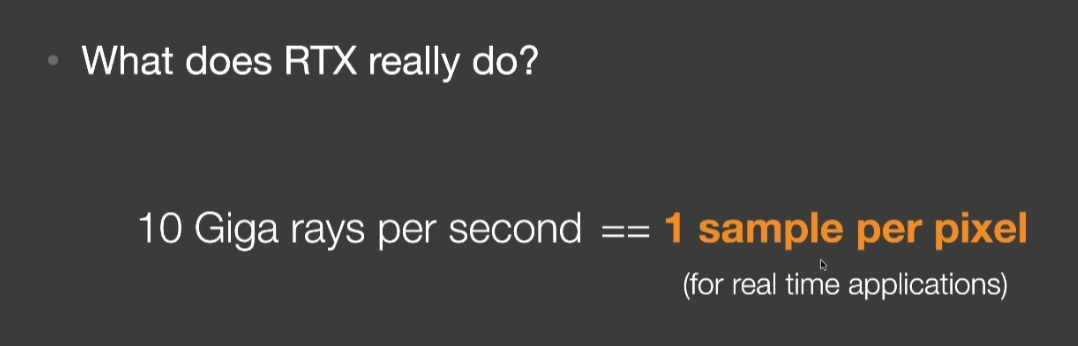



- 实时光线追踪(RTRT)和Path Tracing基本上只有算法上的简化,并没有需要新的算法,本身的突破是因为硬件的能力增加
- RTRT最大的问题是需要降噪

- 针对RTRT的降噪是非常少的
工业界的做法
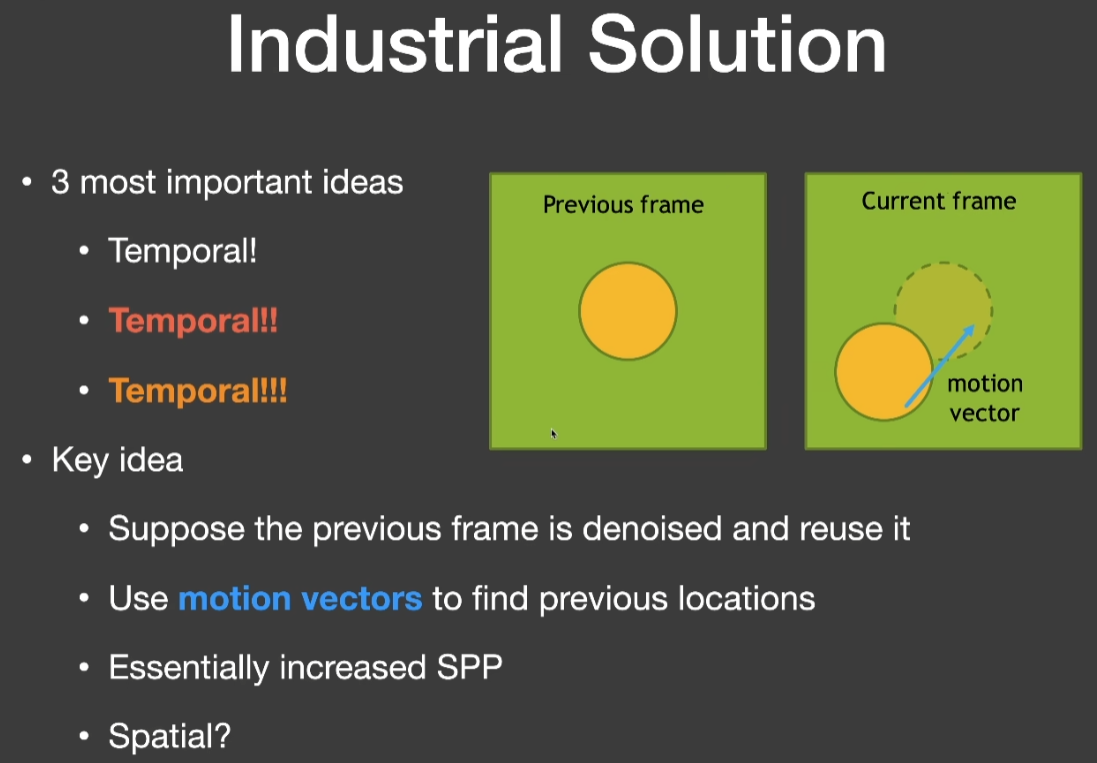
- Temporal
- 即时间上的滤波
- 关键点:
- 用递归的思维来考虑
- 考虑当前帧,认为当前帧的前一帧是已经滤波好了的
- 假设当前场景的运动是连续的
- 用Motion vector找到之前的对应
The G-Buffers

- Geometry buffer
- 几何缓冲区
- 屏幕空间的信息
- 在渲染场景的过程中,认为可以免费得到一些额外的信息
Back Projection

- 求这一帧某个点的像素对应上一帧在哪个点的方法

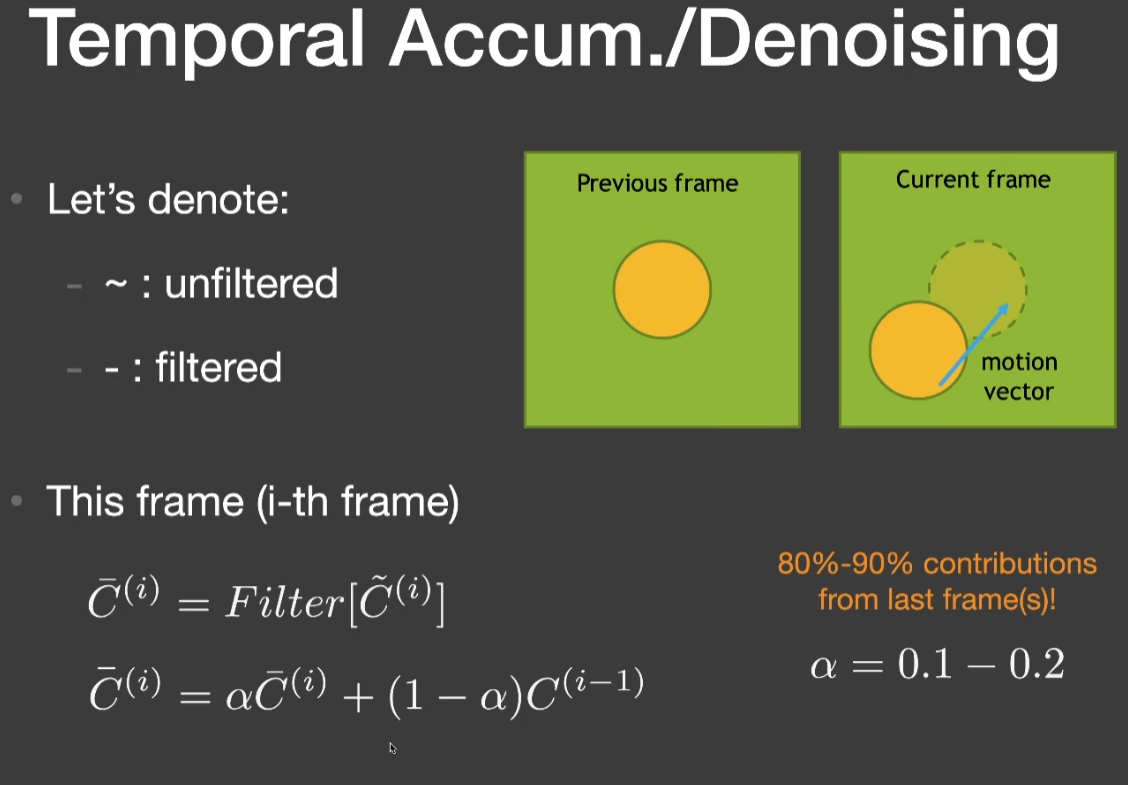
- 通过Back Projection方法做出motion vector后,只需做一个线性的blending就好
Temporal Failure


- screen space的问题,存的信息都在屏幕空间上
- 强行用上一帧信息:拖尾、拖影

Lecture 13 Real-Time Ray-Tracing 2

屏幕空间的低通滤波

- 滤波就是做一种模糊操作
- 低通滤波隐藏着两个问题
- 高频中也有信号,如果把高频的噪声去掉,会造成高频信息的丢失
- 噪声也有低频的

- 高斯滤波,j应该贡献多少到i上去
- 对任何一个像素,定义两个变量
- 一个叫所有权值的和,一个叫所有的加权了的贡献和
- 对于任何一个像素,都要考虑周围或小或大的一圈像素j,应该如何贡献到i上
- 归一化




- 用更多的feature指导滤波过程


解大的滤波

- 第一种解法
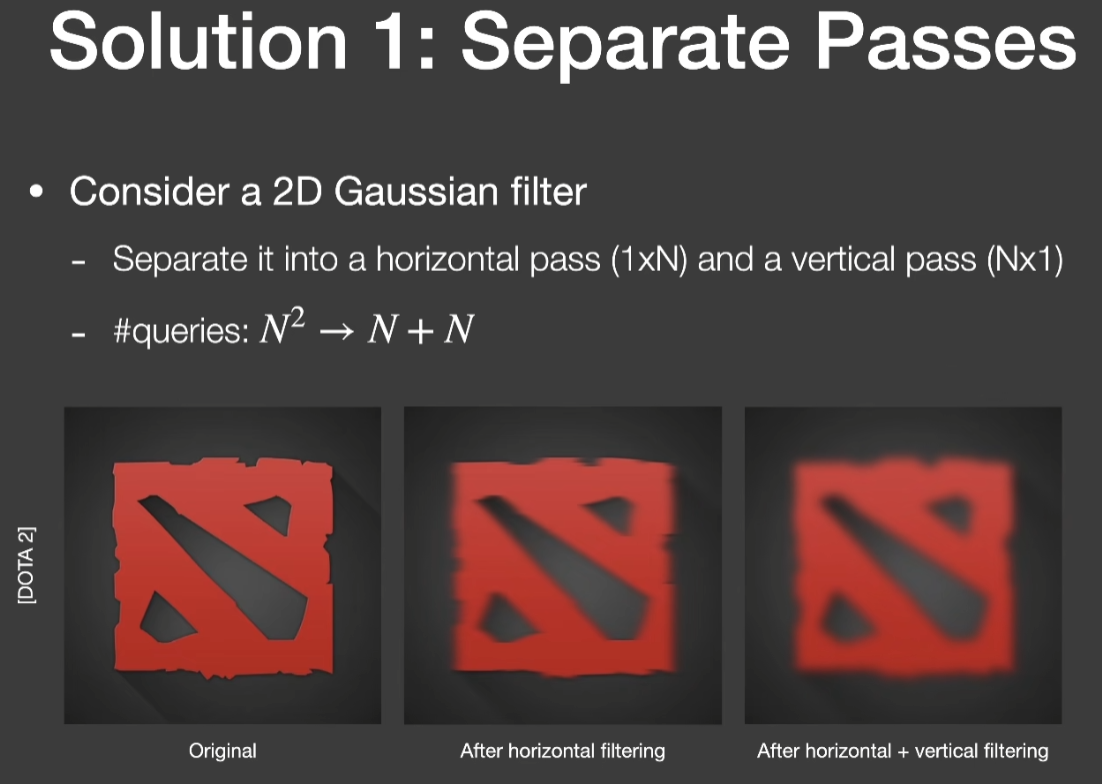

- 因为二维的高斯函数在数学上就是可拆分的
- 滤波就是在做卷积
- 但是理论上复杂的滤波拆分不出来
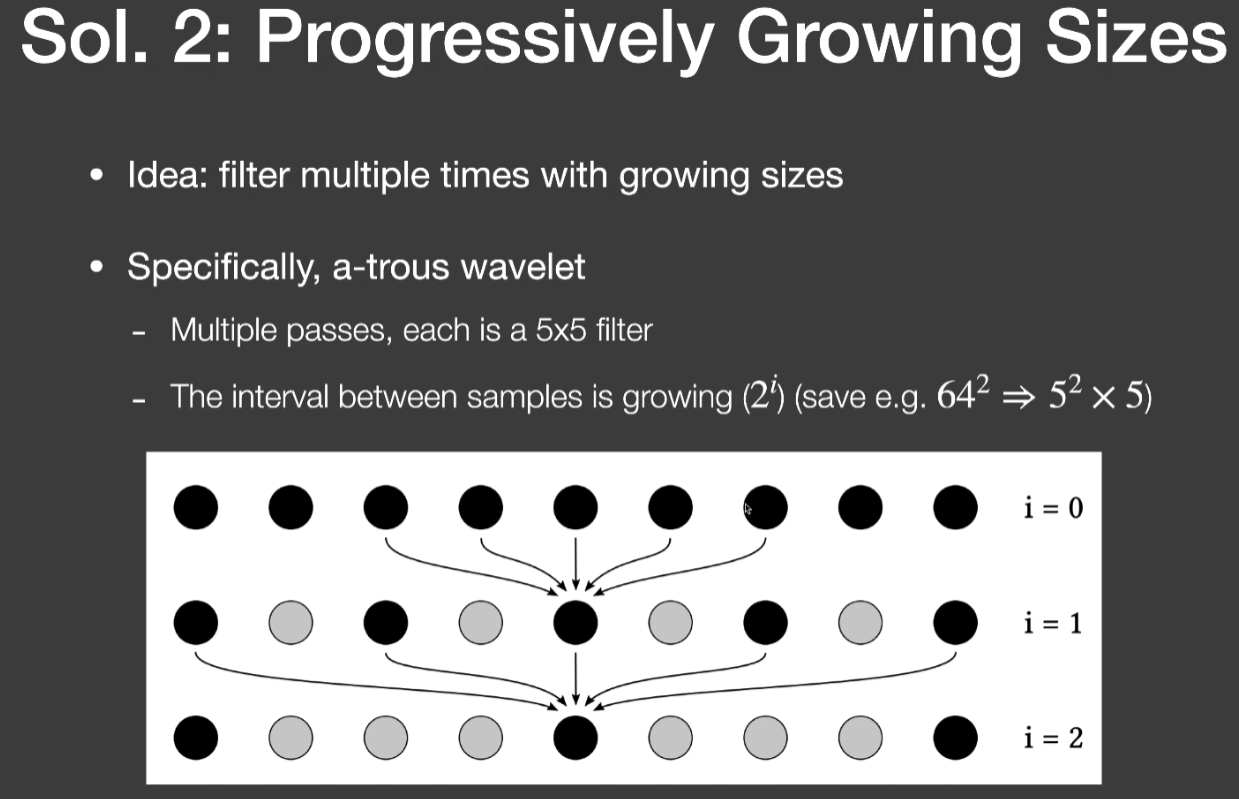
- 第二种解法
- 用一个逐步增大的filter做多趟的path
- 例子:a-trous wavelet (一个filter名)
- 每一趟的间隔变大,但考虑的像素还是5个
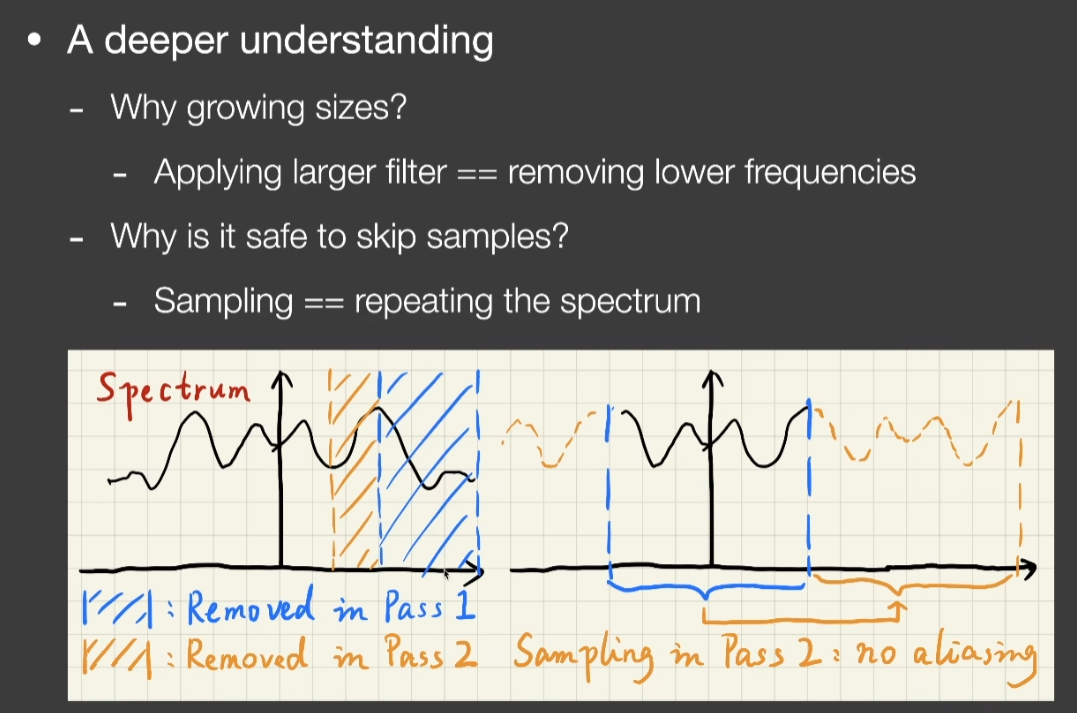
- 为什么要用越来越大的filter
- 用大的filter意味着要去除低的频率
- 为什么可以跳过样本
- 采样在频域上是在做搬移频谱,搬移的距离正好是2倍的上一趟最高频率,不会出现混叠(aliasing)
Outlier Removal (and Clamping)

- 超级量的点在filter后会变成更大的量点


- 处理:
- 对每个像素取周围7x7
- 每个像素都得到7x7范围内的均值和方差
- 认为像素的颜色都应该集中在均值±若干个方差范围内,超出这个范围的值都认为是outlier,都claimp到这个范围
- 把上一帧的结果clamp到当前帧统计学的范围附近,上一帧的结果不愿意多相信它,把它clamp向当前帧
Lecture 14 A Glimpse of industrial Solution


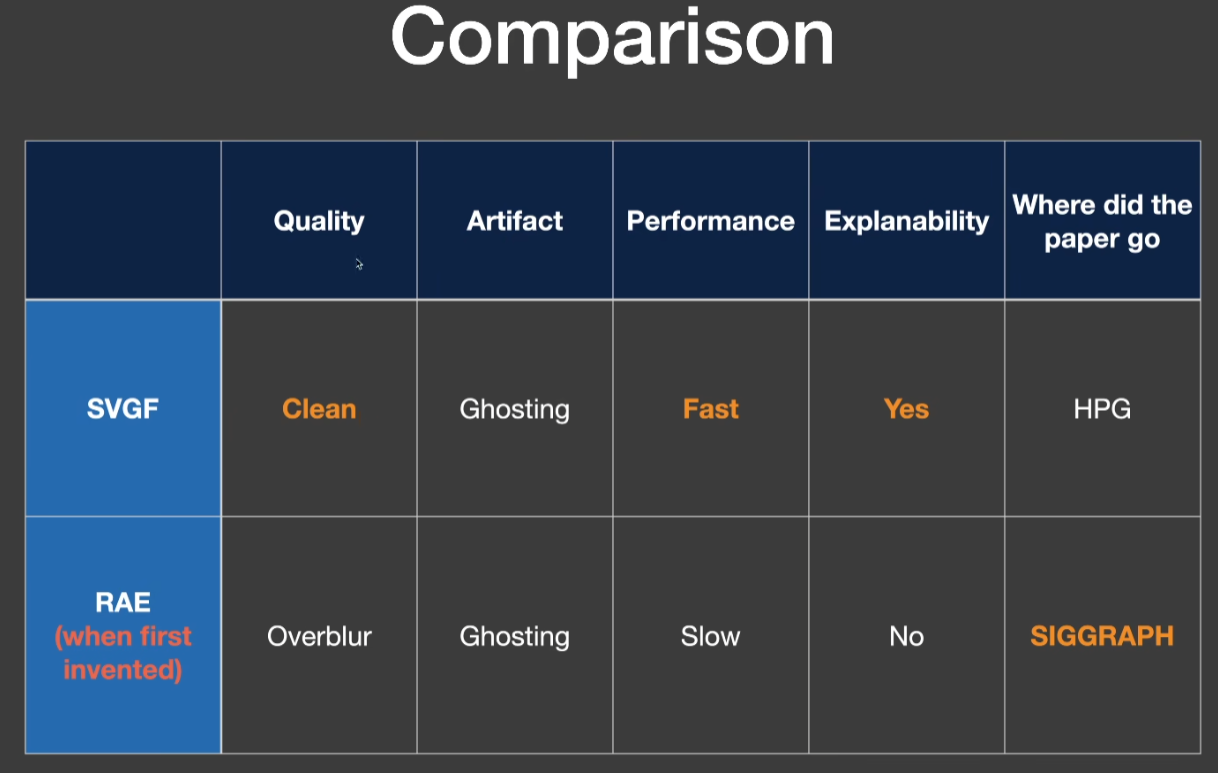
SVGF



RAE

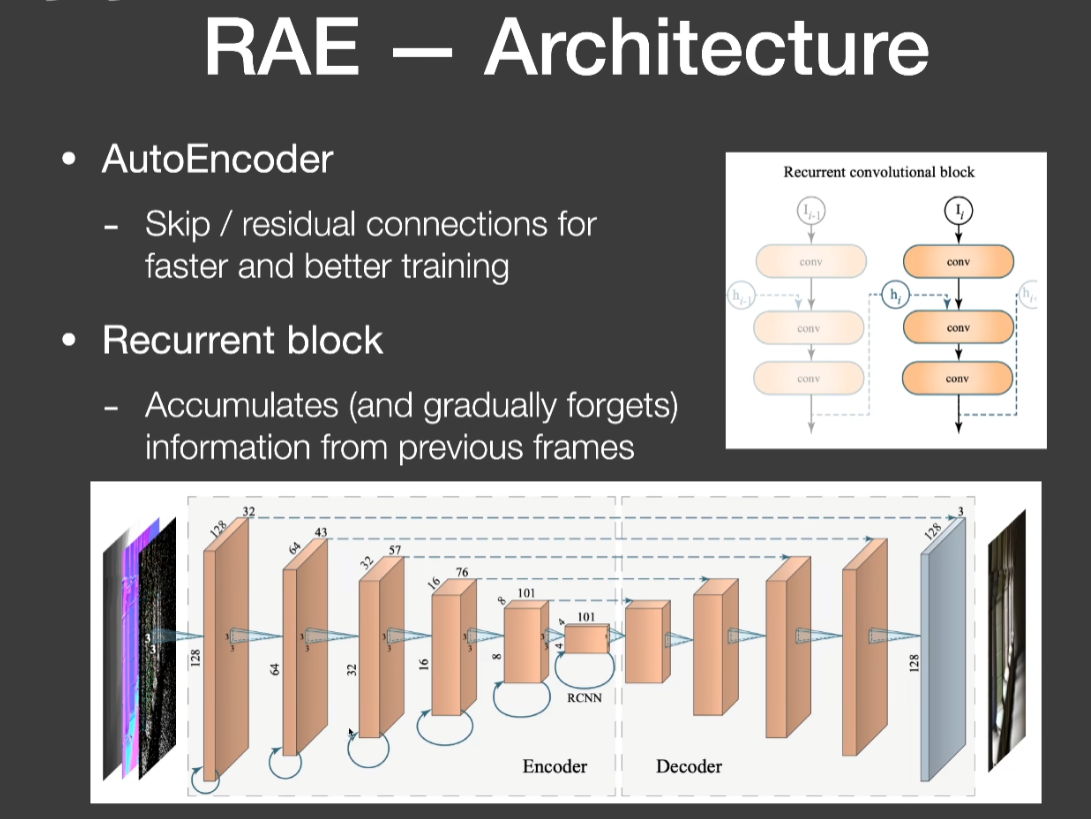

- 残影、overblur
Temporal Anti-Aliasing (TAA)
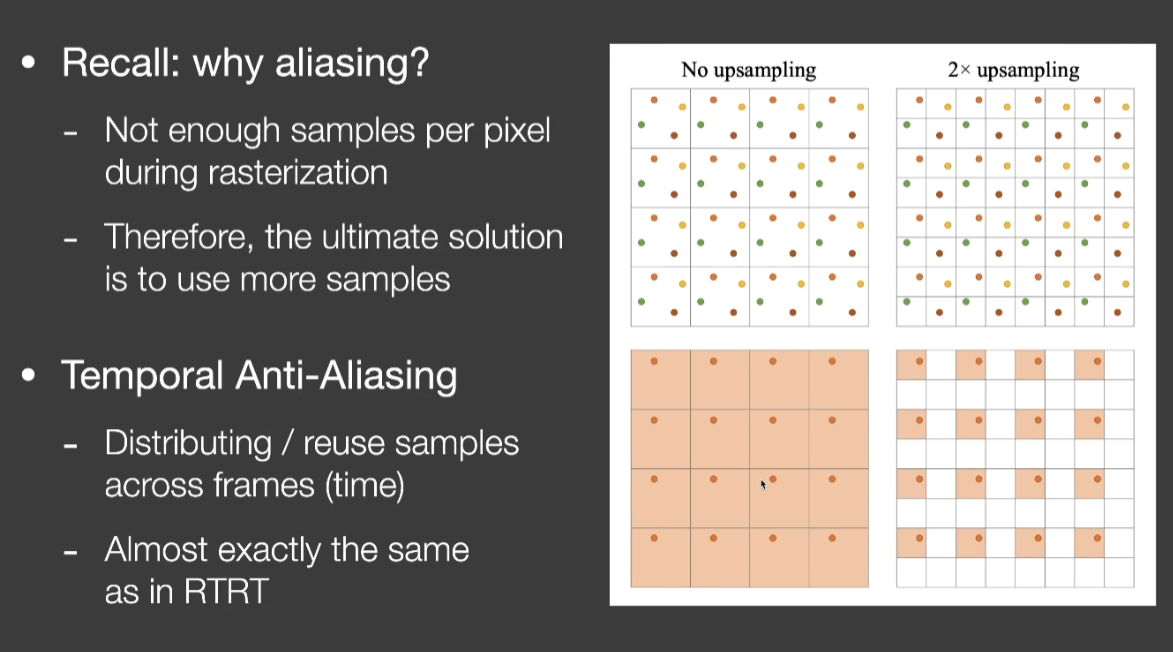
- 走样是因为样本不足
- TAA是从复用上一帧的一些sample,当前帧仍然使用1个SPB,思路跟RTRT使用temporal信息一模一样

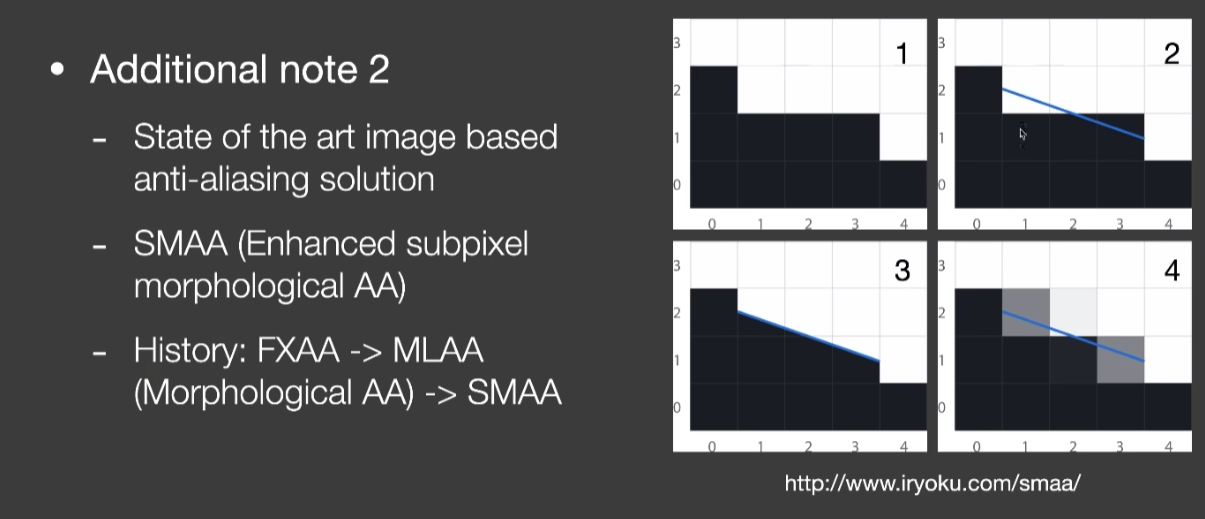

- 有意义的数值不能反走样,图像可以反走样

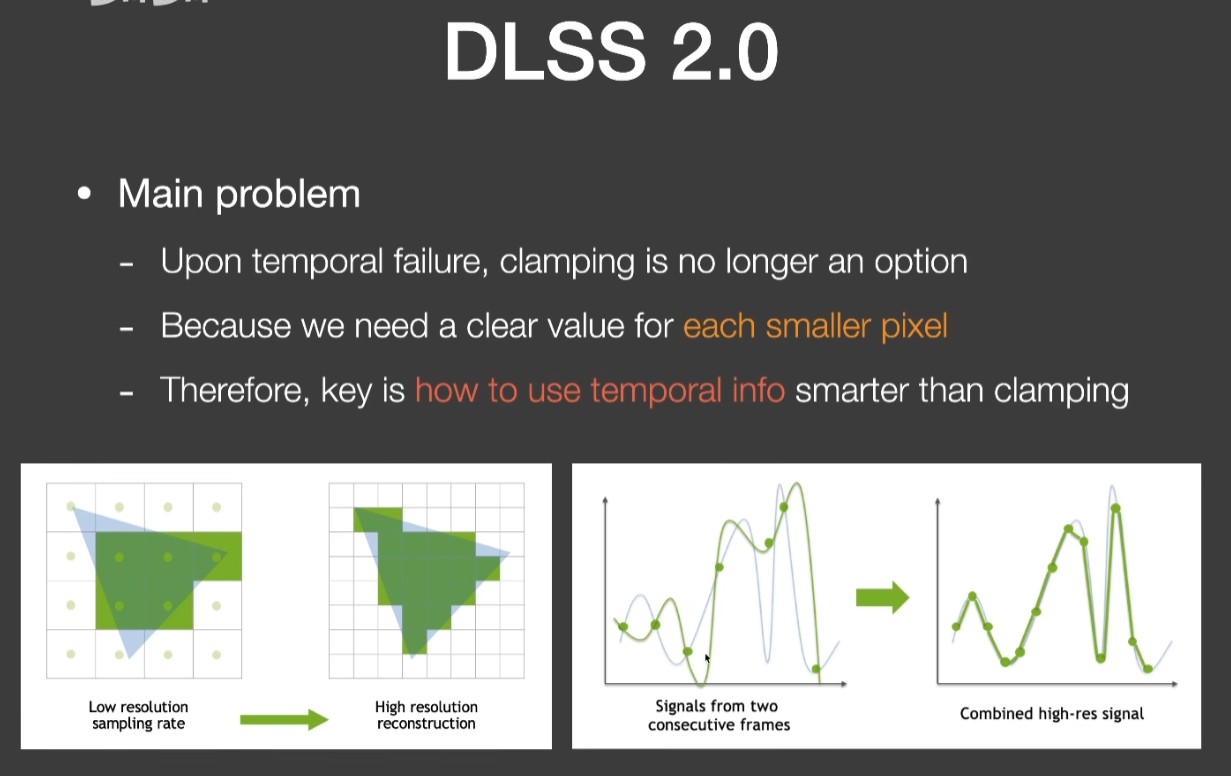

Deferred Shading
- 延迟渲染


- 基本解决思路:
- 把场景渲染(光栅化)两次
- 第一次光栅化不做shading,任何的fragment只用来做对深度缓存的更新
- 第二次做shading,只有深度等于深度缓存的地方,才能通过测试
- 问题:做不了AA,但能用TAA或图像空间AA解决
Tiled Shading
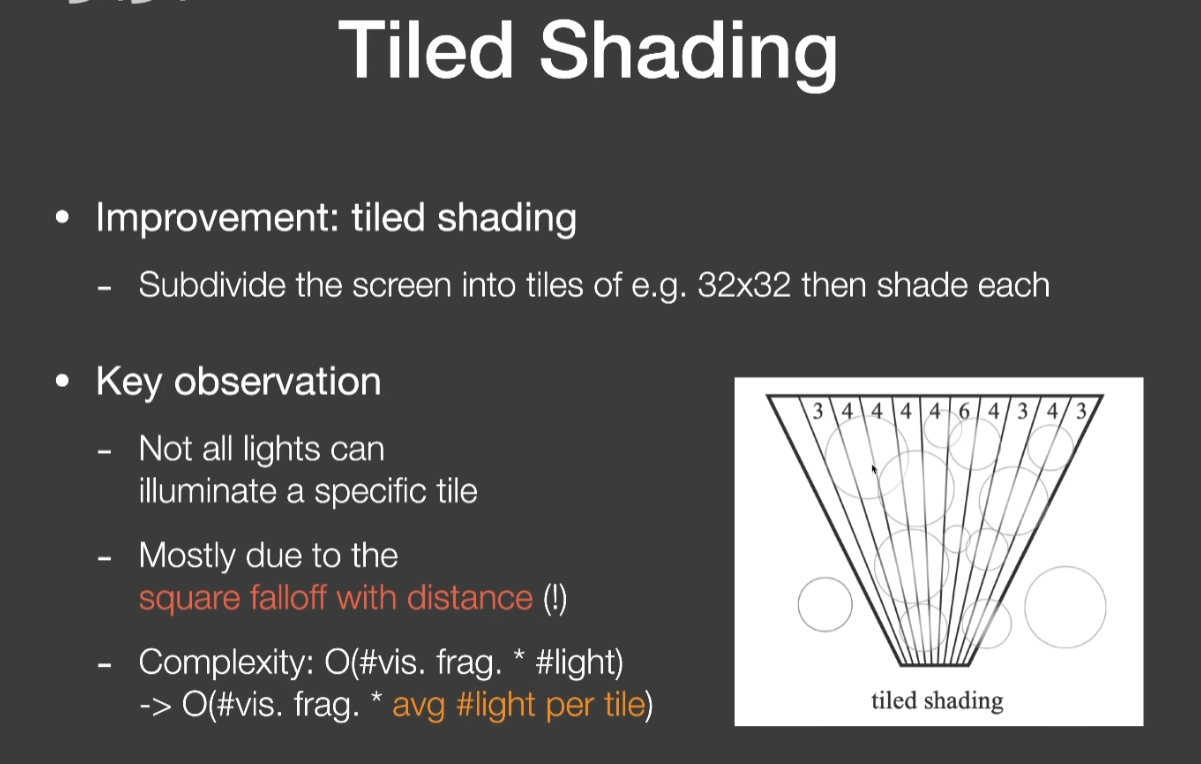
- 把屏幕分成小块,每个小块单独做shading
- 通过这种方法,可以节省每个小块需要考虑的光源数量
- 把每块光源的数量降低到平均的光源数量
Clustered Shading
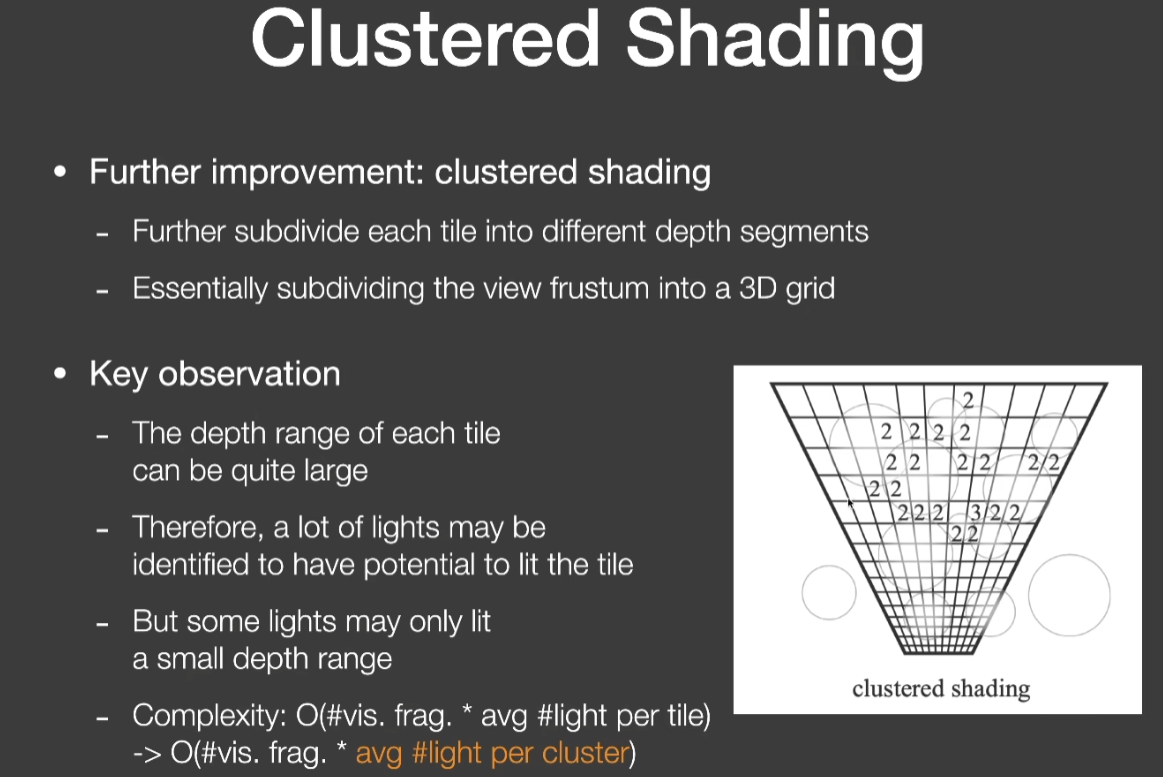
- 不止把屏幕空间分成若干块,还要在深度上切片,避免没有意义的Shading
Level of Detail Solutions

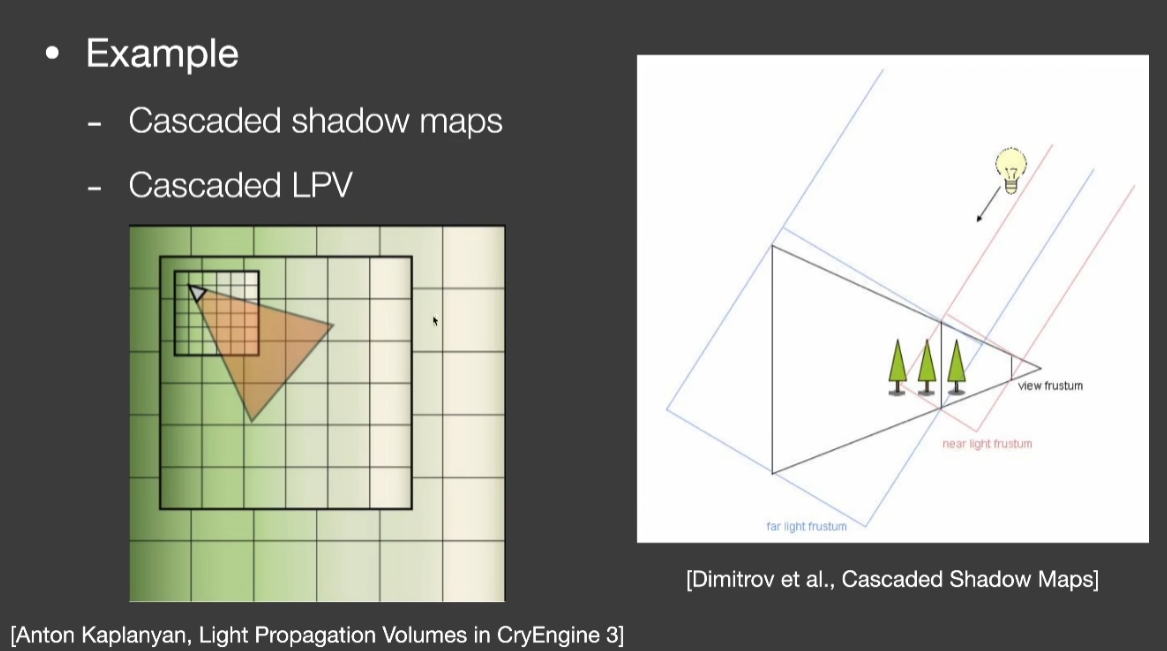


Global Illumunation Solutions



