uni_shiki

数学可视化(10)——Lambert漫反射模型

  • 2023-11-21
  • 作者 uni_shiki
  • ~4.67K 字
  1. 1. 光照模型
  2. 2. Lambert光照模型

 

光照模型

  • 分为经验光照模型、通用光照模型

  • 经验光照模型（模拟光照，局部光照模型）

    • Lambert
    • HalfLambert
    • Phong
    • Blin-Phone
    • Cook-Torrance
    • …

  • 光照分量是叠加的

    • Itotal = Iamb + Idiff + Ispec
    • Iamb 环境光
    • Idiff 漫反射光
    • Ispec 镜面反射光

  • 通用光照模型（真实光照，全局光照模型）

Lambert光照模型

  • 当光照射到理想的漫反射体上时，漫反射光强与入射光方向和入射点的法向量之间的夹角余弦成正比。在0°~90°范围内，夹角越大，漫反射的光线越少。且反射的光强不会随着观察者角度不同发生改变

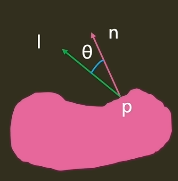
  • Idiff = max((n·l),0) mdiff * sdiff
  • n为光线入射点物体表面的法向量
  • l为光向量方向
  • mdiff为材质漫反射颜色
  • sdiff为光源漫反射颜色
  • 颜色的操作分为加色与减色
  • 一般加色对应加法，减色对应乘法
  • m与s项都是可以通过预定义得到的
  • 物体受光点表面的法线是需要我们计算的
  • 因此求物体的漫反射光照情况的前提是，要计算出物体表面各个点的法线
  • 由于在SDF下定义一个特定点的参数曲面是f(p)=0,因此可以通过该表面上的点的SDF梯度来计算该等值面的法线，也就是分别计算f(p)在xyz3个方向的偏导数
  • 比较简单的方法是，可以利用梯度的定义给物体表面p点的某一个方向加上一个很小的epsilon值，来计算某个方向的前项微分值，但可能会存在后项差异

  • 因此，我们可以将前项与后项微分的值相加除以二来消除这种后项微分可能性的差异，得到更精确的结果

  • 因此一个比较精确的法线值，可以通过以下公式计算得到

  • 这种方式虽然说计算比较精确，但需要6次的f(p)计算。在不考虑精确度的情况下，使用前项微分替代的话。需要计算4次f(p)的值

用前项微分替代

  • 而如果在假设 f(p) = 0 的前提下，可以进一步简化

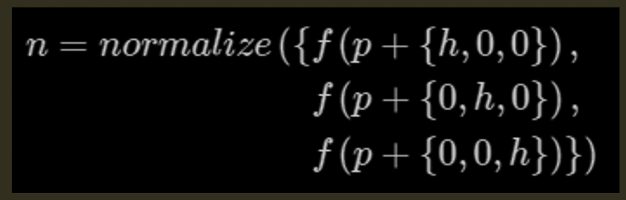
  • 考虑到条件苛刻与精度的前提下，有另外一种比较好的替代方案，同样采用中心差异梯度定义的技术，利用四面体技术通过4次f(p)的计算，就可以达到6次计算的精度。这种方法也是目前大多数情况下比较通用的计算法线的方法

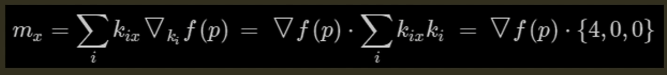
Paulo Falcao的四面体技术优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
...
//通过中心差异的到的比较精确的值
         float3 GetNormal1(float3 p)
         {
             float2 e = float2(EPSILON,0.0);
             float fdx = sdScene(p+e.xyy) - sdScene(p-e.xyy);
             float fdy = sdScene(p+e.yxy) - sdScene(p-e.yxy);
             float fdz = sdScene(p+e.yyx) - sdScene(p-e.yyx);
             return normalize(float3(fdx,fdy,fdz));
         }
         
         //利用前向微分
         float3 GetNormal2(float3 p)
         {
             float d = sdScene(p);
             float2 e = float2(EPSILON,0.0);
             float fdx = sdScene(p+e.xyy) - d;
             float fdy = sdScene(p+e.yxy) - d;
             float fdz = sdScene(p+e.yyx) - d;
             return normalize(float3(fdx,fdy,fdz));
         }
         
         //Paulo Falcao的四面体技术优化
         float3 GetNormal3(float3 p)
         {
             float2 k = float2(1, -1);
             return normalize(k.xyy*sdScene(p+k.xyy*EPSILON)
                 + k.yxy*sdScene(p+k.yxy*EPSILON)
                 + k.yyx*sdScene(p+k.yyx*EPSILON)
                 + k.xxx*sdScene(p+k.xxx*EPSILON));
         }
         ...

          if(dist<MAX_DIST)
             {
                 // 利用预定义的光源位置与着色点位置计算光源方向
                 float3 p = camPos+rayDir*dist;
                 float3 lightPos = float3(3.0,5.0,-5.0);
                 float3 lightdirI = normalize(lightPos-p);
                 float3 n = GetNormal3(p);

                 // 利用Lambert法则计算着色点的漫反射值
                 float3 diffuse = max(dot(n,lightdirI), 0);
                 c += diffuse;
             }

  • 模型的背部过于黑了，这是由于Lambert模型将漫反射强度，也就是dot(n,l)的值，范围映射本身在[-1，1]间，我们用max()函数强制截断到了[0，1]
  • 如果将dot(n,l)的值*0.5+0.5映射到[0,1]区间，这样Lambert模型计算出的光照结果值大于0
1
float3 diffuse = max(dot(n,lightdirI)*0.5+0.5, 0);

  • 这样物体本身提升了亮度
  • 这就是Half Lambert光照模型了
  • 也可以利用经验光照模型中的环境光分量的方式做到这一点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 光照模型
// Lambert光照模型
         float3 Lambert(float3 lightDir, float3 normal, float3 lightColor, float3 diffuseColor)
         {
             return lightColor * diffuseColor * max(0.0, dot(normal, lightDir));
         }
         // HalfLambert光照模型
         float3 HalfLambert(float3 lightDir, float3 normal, float3 lightColor, float3 diffuseColor)
         {
             return lightColor * diffuseColor * max(0.0, dot(normal, lightDir)*0.5 + 0.5);
         }
         // Phong光照模型
         float3 Phong(float3 lightDir, float3 normal, float3 viewDir, float shininess, float3 lightColor, float3 specularColor)
         {
             float3 reflectDir = reflect(-lightDir, normal);
             return lightColor * specularColor * pow(max(0.0, dot(reflectDir, viewDir)), shininess);
         }
         // BlinnPhong光照模型
         float3 BlinnPhong(float3 lightDir, float3 normal, float3 viewDir, float shininess, float3 lightColor, float3 specularColor)
         {
             float3 halfDir = normalize(lightDir + viewDir);
             return lightColor * specularColor * pow(max(0.0, dot(normal, halfDir)), shininess);
         }

         ...

         	// 利用预定义的光源位置与着色点位置计算光源方向
                 float3 p = camPos+rayDir*dist;
                 float3 lightPos = float3(3.0,5.0,-5.0);
                 float3 lightdirI = normalize(lightPos-p);
                 float3 n = GetNormal3(p);
                 
                 float3 matColor = float3(0.5, 0.5, 0.5); 
                 float3 lightColor = float3(1.0, 1.0, 1.0);
                 float3 ambient = float3(0.2, 0.2, 0.2);
                 float3 diffuse = Lambert(lightdirI, n, lightColor, matColor);
                 float3 specular = BlinnPhong(lightdirI, n, -rayDir, 32.0, lightColor, matColor);
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可
,
最后编辑：2024-03-26