1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
| Shader "MathematicalVisualizationArt/MyLearning09"
{
Properties
{
}
SubShader
{
Tags{"RenderType" = "Transparent" "RenderPipeline" = "UniversalRenderPipeline" "IgnoreProjector" = "True"}
LOD 300
Pass
{
Name "DefaultPass"
HLSLPROGRAM
struct Attributes
{
float4 positionOS : POSITION;
float2 uv : TEXCOORD0;
};
struct Varyings
{
float2 uv : TEXCOORD0;
float4 positionCS : SV_POSITION;
float4 screenPos : TEXCOORD1;
};
Varyings vert (Attributes input)
{
Varyings output = (Varyings)0;
VertexPositionInputs vertexInput = GetVertexPositionInputs(input.positionOS.xyz);
output.uv = input.uv;
output.positionCS = vertexInput.positionCS;
output.screenPos = ComputeScreenPos(vertexInput.positionCS);
return output;
}
// 一、定义数据
// 二、定义三维几何体sdf
// 球体sdf
float sdSphere( float3 p, float r )
{
return length(p)-r;
}
// 平面sdf
float sdPlane( float3 p, float3 n, float h )
{
// n must be normalized
n = normalize(n);
return dot(p,n) + h;
}
// 圆环sdf
float sdTorus( float3 p, float2 t )
{
float2 q = float2(length(p.xz)-t.x,p.y);
return length(q)-t.y;
}
// 圆锥sdf
float sdCone( float3 p, float2 c, float h )
{
// c is the sin/cos of the angle, h is height
// Alternatively pass q instead of (c,h),
// which is the point at the base in 2D
float2 q = h*float2(c.x/c.y,-1.0);
float2 w = float2( length(p.xz), p.y );
float2 a = w - q*clamp( dot(w,q)/dot(q,q), 0.0, 1.0 );
float2 b = w - q*float2( clamp( w.x/q.x, 0.0, 1.0 ), 1.0 );
float k = sign( q.y );
float d = min(dot( a, a ),dot(b, b));
float s = max( k*(w.x*q.y-w.y*q.x),k*(w.y-q.y) );
return sqrt(d)*sign(s);
}
// 圆角盒sdf
float sdRoundBox( float3 p, float3 b, float r )
{
float3 q = abs(p) - b;
return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0) - r;
}
// scene sdf
// 用于计算CSG几何运算后的场景结果
float sdScene(float3 p)
{
//定义球体
float3 spherePos = float3(1.5, 1.0, 0.0);
float sphereRadius = 1.0;
float3 sphereNormal = normalize( p - spherePos );
//定义圆角盒
float3 boxPos = float3(-1.5, 0.5, 0.0);
float3 boxSize = float3(1.0, 0.5, 0.5);
float boxRadius = 0.1;
//定义圆环
float3 torusPos = float3(5.0, 1.0, 0.0);
float2 torusRadius = float2(0.8, 0.3);
//定义圆锥
float3 conePos = float3(-5.0, 2.0, 0.0);
float2 coneRadius = float2(0.1, 0.3);
float coneHeight = 2.0;
//定义平面
float3 planePos = float3(0.0, 0.0, 0.0);
float3 planeNormal = float3(0.0, 1.0, 0.0);
//求交集
float sphereDist = sdSphere(p - spherePos, sphereRadius);
float torusDist = sdTorus(p - torusPos, torusRadius);
float coneDist = sdCone(p - conePos, coneRadius, coneHeight);
float planeDist = sdPlane(p - planePos, planeNormal, 0.0);
float boxDist = sdRoundBox(p - boxPos, boxSize, boxRadius);
return min(min(min(min(sphereDist, boxDist),coneDist),torusDist),planeDist);
}
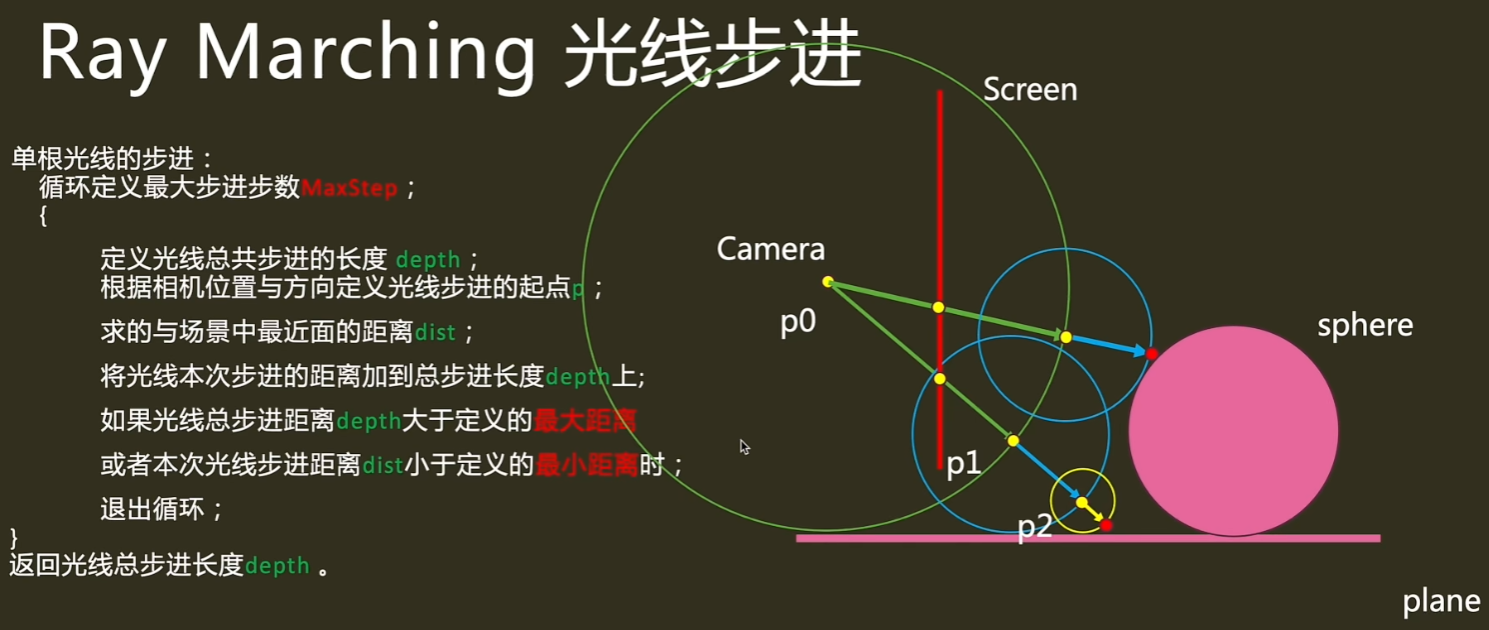
// RayMarch, 用于计算光线与物体的交点
// 输入分别是摄像机位置与光线方向
float RayMarch(float3 ro, float3 rd)
{
float depth = 0.0;
for(int i = 0; i < MAX_MARCHING_STEPS; i++)
{
float3 p = ro + rd*depth;
float dist = sdScene(p);
depth+=dist;
if(depth > MAX_DIST || dist < MIN_DIST)
break;
}
return depth;
}
half3 PixelColor(float2 uv)
{
half3 c = half3(0, 0, 0);
//
float uvSizeScale = 1;
//四象限转一象限
uv.y = 1.0- uv.y;
//全象限 (-5, 5)
uv = (uv*2.0 -1.0)*uvSizeScale;
//消除屏幕拉伸影响
half co = width/height;
uv = float2(uv.x*co, uv.y);
// 根据摄像机位置与uv坐标计算出光线方向
//定义摄像机
float3 camPos = float3(0.0, 1.0, -5.0);
float3 lightDir = normalize(float3(uv, 1.0));
float dist = RayMarch(camPos, lightDir); // 步进距离总和(深度)
c = half3(dist/(20-time), dist/(20-time), dist/(20-time));
return c;
}
half4 frag(Varyings input) : SV_Target
{
float2 screenUV = GetNormalizedScreenSpaceUV(input.positionCS);
screenUV = screenUV * float2(1.0, -1.0) + float2(0.0, 1.0);
half3 col = Gamma22ToLinear(PixelColor(screenUV));
return half4(col, 1);
}
ENDHLSL
}
}
}
|