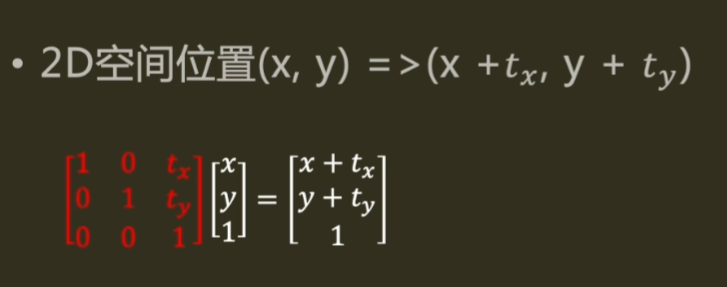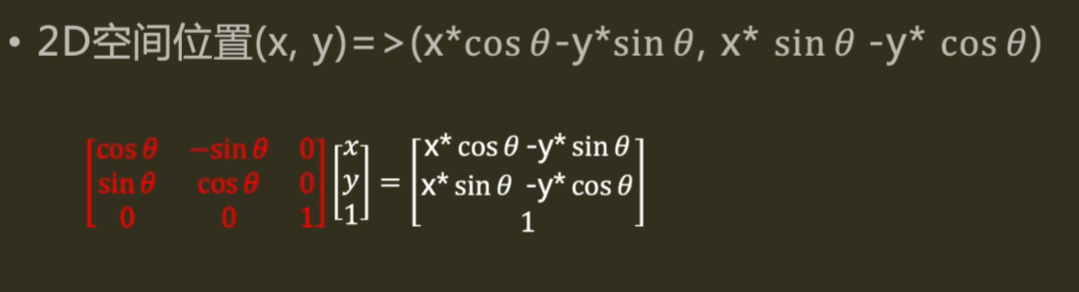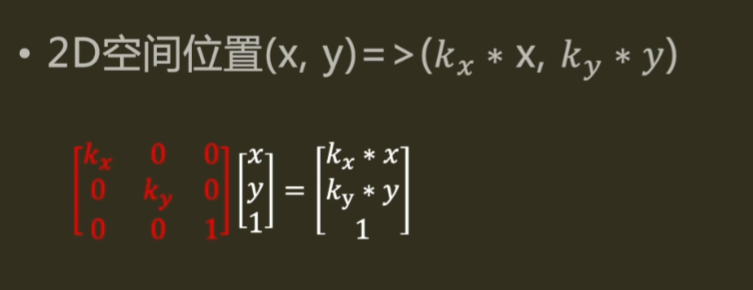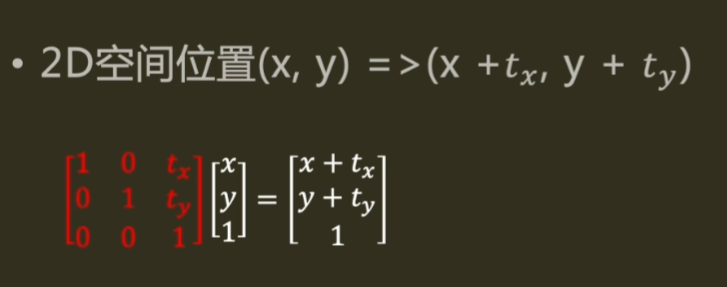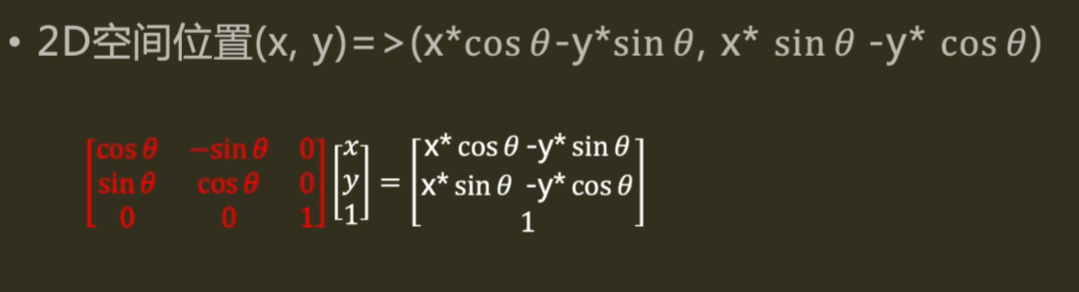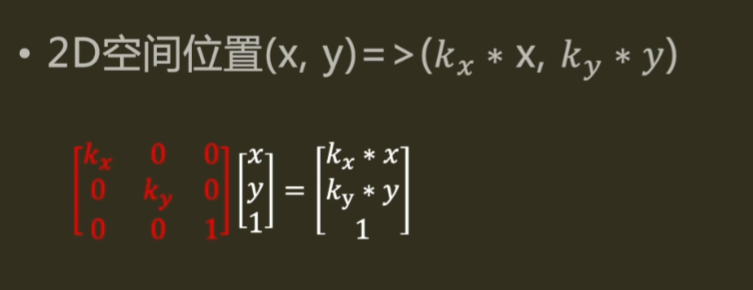1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| float sdStar5(in float2 p, in float r, in float rf)
{
const float2 k1 = float2(0.809016994375, -0.587785252292);
const float2 k2 = float2(-k1.x,k1.y);
p.x = abs(p.x);
p -= 2.0*max(dot(k1,p),0.0)*k1;
p -= 2.0*max(dot(k2,p),0.0)*k2;
p.x = abs(p.x);
p.y -= r;
float2 ba = rf*float2(-k1.y,k1.x) - float2(0,1);
float hh = clamp( dot(p,ba)/dot(ba,ba), 0.0, r );
return length(p-ba*hh) * sign(p.y*ba.x-p.x*ba.y);
}
float3x3 move2d(float2 p)
{
return float3x3(1, 0, p.x,
0, 1, p.y,
0, 0, 1 );
}
float3x3 rotate2d(float2 a)
{
float c = cos(a);
float s = sin(a);
return float3x3(c, -s, 0,
s, c, 0,
0, 0, 1);
}
float3x3 scale2d(float2 s)
{
return float3x3(1/s.x, 0, 0,
0, 1/s.y, 0,
0, 0, 1);
}
half3 PixelColor(float2 uv)
{
half3 c = half3(0, 0, 0);
//---编写你的逻辑, 不要超过2023个字节(包括空格)
// 全象限
uv.y = 1.0 - uv.y;
uv = uv * 2 - 1;
// (-5,5)
const int uvScale = 5;
uv = uv * uvScale;
// 消除屏幕拉伸影响
half co = w/h;
uv = float2(uv.x * co, uv.y);
float step = 1.0 / w;
// 绕半径为5的圆心做平移
float3 pos = mul(move2d(float2(cos(time), sin(time)) * 5), float3(uv, 1));
// 旋转
pos = mul(rotate2d(cos(time)*5), pos);
// 缩放
pos = mul(scale2d(float2(cos(time) + 2, cos(time) + 2)), pos);
float star5 = smoothstep(step, -step, sdStar5(pos.xy, 1, 2.5));
c = lerp(c, float3(1.0, 1.0, 1.0), star5);
//
return c;
}
|