uni_shiki

数学可视化(04)——极坐标系与函数拟合

  • 2023-11-05
  • 作者 uni_shiki
  • 932 字
  1. 1. 极坐标系
  2. 2. 函数拟合
    1. 2.1. 函数拟合的步骤
    2. 2.2. 图形学中的函数拟合的方法

 

极坐标系

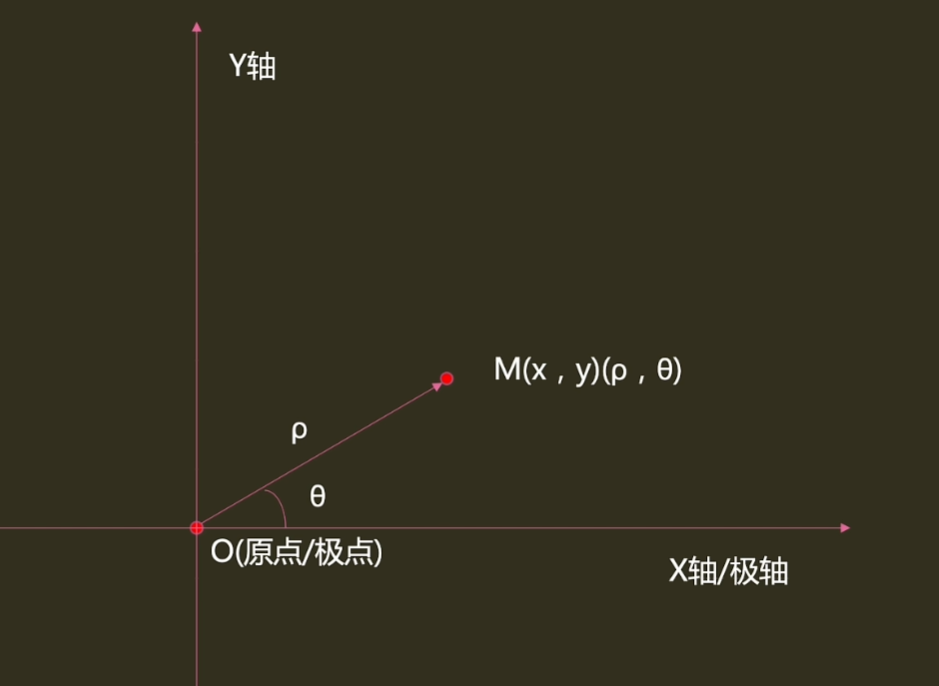
  • 定义M点离极点的距离为极径ρ，向量M与极轴夹角为Θ
  • 可以容易得到M点在两个坐标系下的相互转化公式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 全象限
uv.y = 1.0 - uv.y;
uv = uv * 2 - 1;
// (-5,5)
const int uvScale = 5;
uv = uv * uvScale;
// 消除屏幕拉伸影响
half co = w/h;
uv = float2(uv.x * co, uv.y);
// 绘制极坐标轴
half axis = smoothstep(0.01, 0.0, abs(uv.y / uvScale)) + smoothstep(0.01, 0.0, abs(uv.x / uvScale));
// 极径
float r = length(uv);
// 极角
float angle = atan2(uv.x, uv.y);
// 定义坐标系下的函数
float a = 1, b = 0, k = 0;
float f = b + a*cos(k*angle);

half plot = 1.0 - step(f, r);
// 绘制
c = axis + plot;

函数拟合

  • 数学是自然的语言，是对客观世界规律的描述（数学建模）
  • 如何图像形状我们都可以用数学的函数集合（函数空间）来表示。而空间完备性就是函数空间是否可以逼近任意函数
  • 闭区间上的连续函数可以用多项式基数一致逼近（泰勒级数）
  • 闭区间上的周期函数可以用三角函数一致逼近（傅立叶级数）
  • 函数拟合其实就是寻找映射、变换、组合的函数过程

函数拟合的步骤

  • 到哪里找？确定某个函数空间
  • 找哪个？度量哪个函数是好的或更好的
  • 怎么找？求解或优化

图形学中的函数拟合的方法

  • 直接法：采样点，最小二乘法寻找最小平方误差的函数，求解待定系数（连续函数）
  • 间接法：多段区间函数拼接（可以是非连续函数的集合）
  • 心型函数

1
float f = 2 - 2 * sin(angle) + sin(angle) * sqrt(abs(cos(angle))) / (sin(angle) + 1.4);
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可
,
最后编辑：2024-03-26