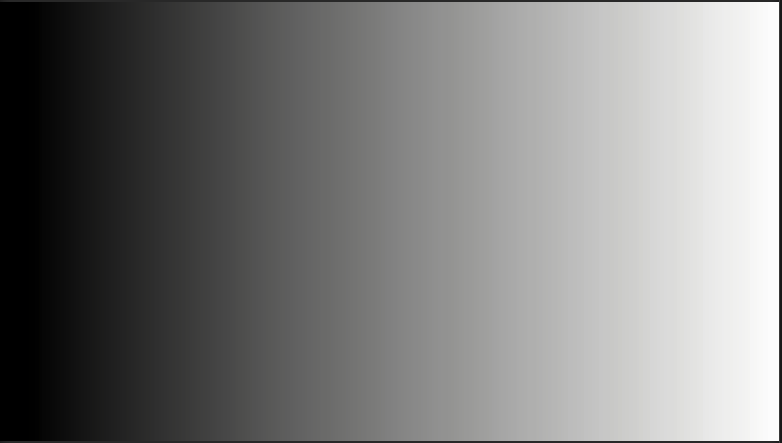本质
- 本质是构造一个造型函数(Sharping Function)
- 输入是一个二维的向量坐标XY,输出是一个三维向量RGB
- 在CPUSample中,输入的是分辨率下的像素索引i,j
- 在GPUSample中,输入的是屏幕坐标u,v
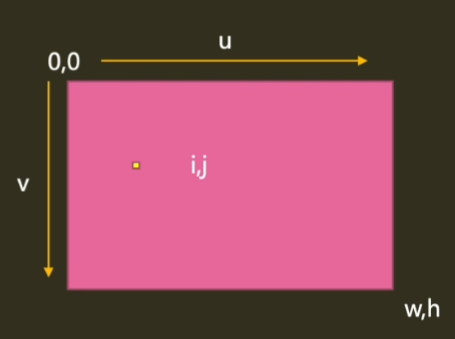
- 也就是说,我们默认屏幕处于正交笛卡尔坐标系的第四象限,即平面直角坐标系下的第四象限
- 造型函数:c.rgb = uv.xxx;
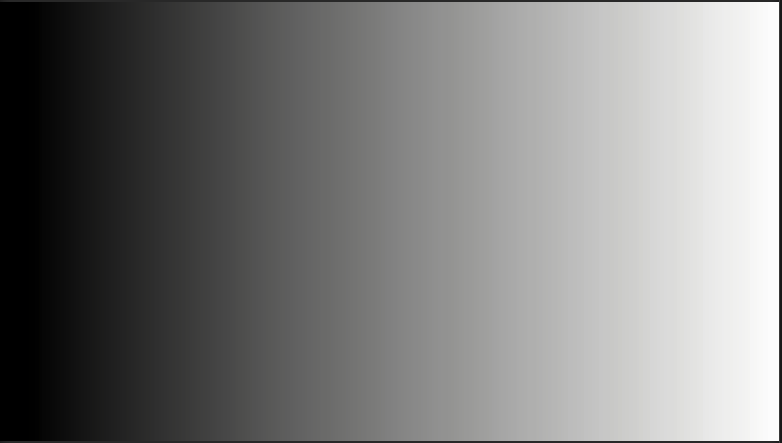
- c.rgb = uv.yyy;

- c.rgb = half3(uv.x, 0, uv.y);

- 第四象限改为第一象限,只需将uv的y方向颠倒即可
- uv.y = 1.0 - uv.y;
- 这样uv的y方向就与Unity默认的y方向就一致了

- 如果想显示整个四个象限,将原点从(0,0)移动到屏幕中心
- 具体做法是:uv = uv * 2.0 - 1.0;
- 这样将[0,1]的区间变成[-1,1]的区间

图形渲染中常用的距离的类型
- 以下都以四象限为例:
- uv = uv * 2.0 - 1.0;
欧式距离


- c = sqrt((pow(uv.y, 2) + pow(uv.x, 2)) * 0.5);
- * 0.5 是为了不出现>1.0的白色的截断的值,使颜色过渡更平滑
曼哈顿距离
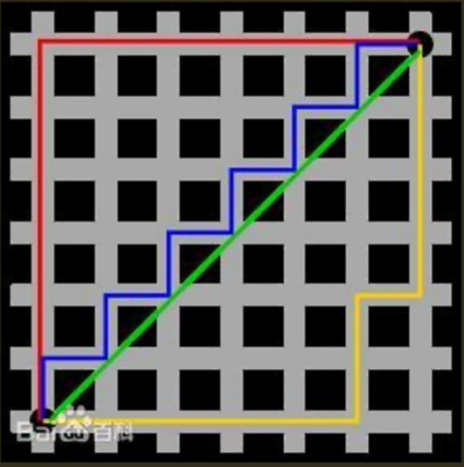
- x、y轴轴距绝对值的总和
- 如上图,绿色的线代表欧式距离,其他线是两点间等效的曼哈顿距离

- c = (abs(uv.y) + abs(uv.x)) * 0.5;
切比雪夫距离

- 也叫做棋盘距离

- c = max(abs(uv.y), abs(uv.x));
马氏距离
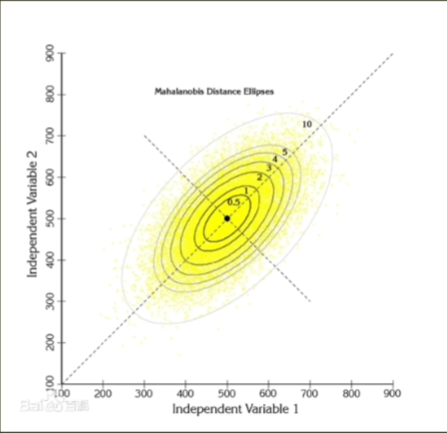
- 是一种特殊的欧氏距离,要考虑不同量度特性间的联系
- 要考虑不同维度间,数据的协方差来计算距离
- 要将量度转换到同一维度下,再计算欧氏距离
- 屏幕的宽度高度属于不同维度,如果不统一量度,会造成图形的拉伸

- 为了图形不被拉伸,需要将宽高转换到同一量度上
- half co = h / w;
c = sqrt((pow(uv.y * co, 2) + pow(uv.x, 2)) * 0.5);